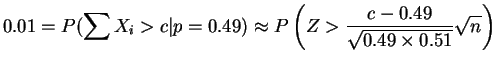 |
So
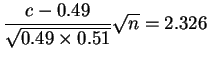 |
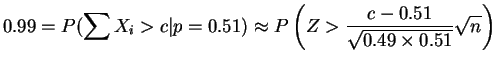 |
So
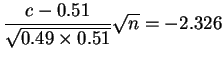 |
So
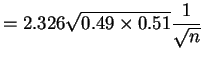 |
||
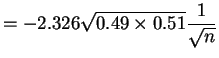 |
or
So
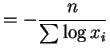 |
||
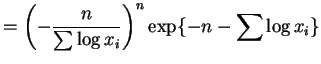 |
and
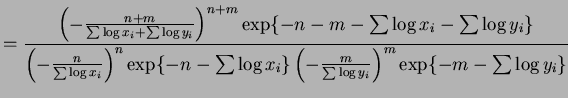 |
||
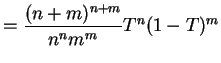 |
So
for suitable
Under ![]() ,
,
![]() are
are ![]() exponential,
so
exponential,
so
![]() Beta
Beta![]() .
.
To find ![]() and
and ![]() either cheat and use equal tail
probabilities (the right thing to do by symmetry if
either cheat and use equal tail
probabilities (the right thing to do by symmetry if ![]() ), or
solve numerically.
), or
solve numerically.
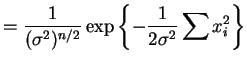 |
||
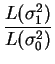 |
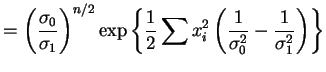 |
If
for some
Under
![]() ,
,
![]() , so
, so
- a.
- For
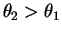
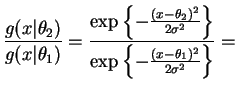 const
const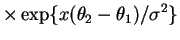
This in increasing in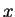 since
since
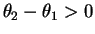 .
.
- b.
- For
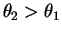
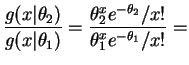 const
const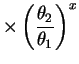
which is increasing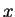 since
since
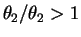 .
.
- c.
- For
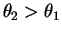
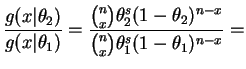 const
const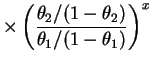
This is increasing in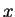 since
since
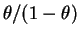 is increasing
in
is increasing
in 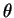 .
.
- a.
-
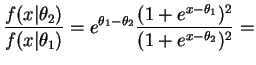 const
const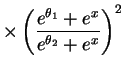
Let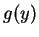
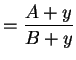
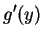
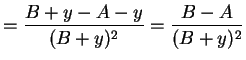
Then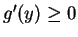 if
if 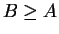 . So we have MLR in
. So we have MLR in 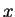 .
.
- b.
- Since the ratio is increasing in
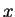 , the most powerful
test is of the form
, the most powerful
test is of the form
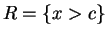 . Now
. Now
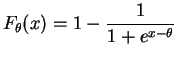
So for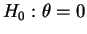 and
and
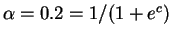 , so
, so
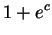
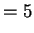
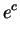
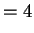
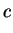
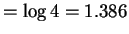
The power is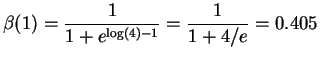
- c.
- Since we have MLR, the test is UMP. This is true for any
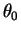 . This only works for
. This only works for 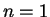 ; otherwise there
is no one-dimensional sufficient statistic.
; otherwise there
is no one-dimensional sufficient statistic.
- a.
-
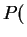
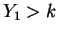 or
or 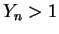
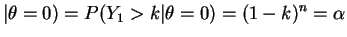
So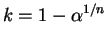 .
.
- b.
-
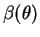
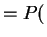
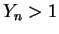 or
or 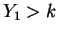
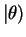
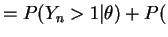
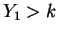 and
and
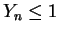
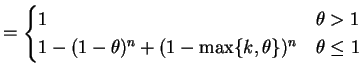
- c.
-
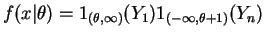
Fix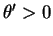 . Suppose
. Suppose
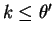 . Then
. Then
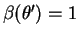 .
.
Suppose
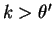 . Take
. Take 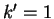 in the NP lemma. Then
in the NP lemma. Then
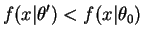
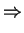
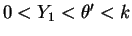 , so
, so
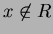
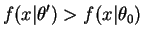
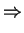
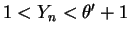 , so
, so 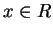
So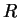 is a NP test for any
is a NP test for any 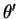 .
.
So
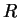 is UMP.
is UMP.
- d.
- The power is one for all
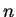 if
if
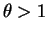 .
.
