



Next: Assignment 10
Up: 22S:194 Statistical Inference II
Previous: Assignment 9
- 9.27
- a.
- The posterior density is
The inverse gamma density is unimodal, so the HPD region is an
interval ![$ [c_1,c_2]$](img553.png) with
with 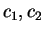 chosen to have equal density
values and
chosen to have equal density
values and
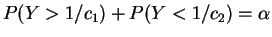 , with
, with
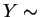 Gamma
Gamma![$ (n+a, [1/b + \sum x_i]^{-1})$](img556.png) .
.
- .b
- The distribution of
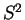 is
Gamma
is
Gamma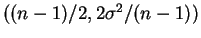 . The resulting posterior density is therefore
. The resulting posterior density is therefore
As in the previous part, the HPD region is an interval that can be
determined by solving a corresponding set of equations.
- c.
- The limiting posterior distribution is
IG
![$ ((n-1)/2,[(n-1)s^2]^{-1})$](img563.png) . The limiting HPD region is
an interval
. The limiting HPD region is
an interval ![$ [c_1,c_2]$](img553.png) with
with
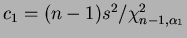 and
and
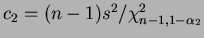 where
where
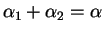 and
and 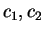 have equal posterior density values.
have equal posterior density values.
- 9.33
- a.
- Since
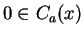 for all
for all 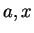 ,
,
For 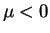 ,
,
if
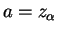 . For
. For 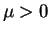 ,
,
if
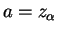 .
.
- b.
- For
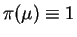 ,
,
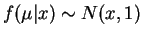 .
.
if
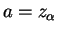 and
and
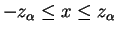 .
For
.
For
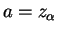 and
and
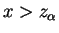 ,
,
as
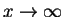 .
.
- 10.1
- The mean is
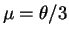 , so the method of moments
estimator is
, so the method of moments
estimator is
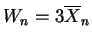 . By the law of large numbers
. By the law of large numbers
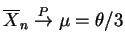 , so
, so
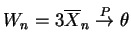 .
.




Next: Assignment 10
Up: 22S:194 Statistical Inference II
Previous: Assignment 9
Luke Tierney
2003-05-04
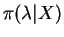
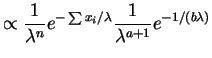
![$\displaystyle = \frac{1}{\lambda^{n+a+1}} e^{-[1/b + \sum x_i]/\lambda}$](img551.png)
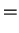 IG
IG![$\displaystyle (n+a, [1/b + \sum x_i]^{-1})$](img552.png)
![$ [c_1,c_2]$](img553.png) with
with 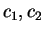 chosen to have equal density
values and
chosen to have equal density
values and
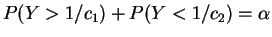 , with
, with
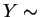 Gamma
Gamma![$ (n+a, [1/b + \sum x_i]^{-1})$](img556.png) .
.
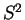 is
Gamma
is
Gamma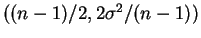 . The resulting posterior density is therefore
. The resulting posterior density is therefore
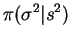
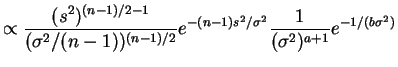
![$\displaystyle \propto \frac{1}{(\sigma^2)^{(n-1)/2 + a + 1}} e^{-[1/b + (n-1)s^2]/\sigma^2}$](img561.png)
 IG
IG![$\displaystyle ((n-1)/2 + a, [1/b + (n-1)s^2]^{-1})$](img562.png)
![$ ((n-1)/2,[(n-1)s^2]^{-1})$](img563.png) . The limiting HPD region is
an interval
. The limiting HPD region is
an interval ![$ [c_1,c_2]$](img553.png) with
with
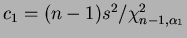 and
and
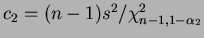 where
where
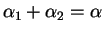 and
and 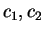 have equal posterior density values.
have equal posterior density values.
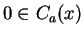 for all
for all 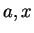 ,
,
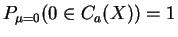
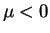 ,
,
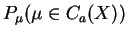
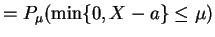
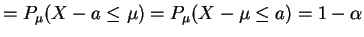
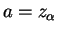 . For
. For 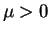 ,
,
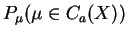
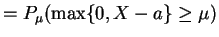
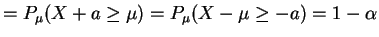
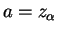 .
.
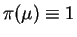 ,
,
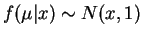 .
.
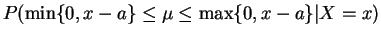
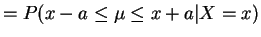
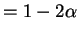
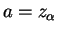 and
and
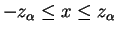 .
For
.
For
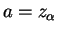 and
and
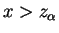 ,
,
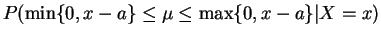
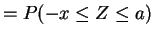
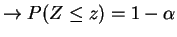
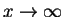 .
.
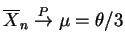 , so
, so
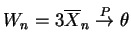 .
.
