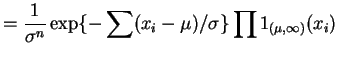 |
||
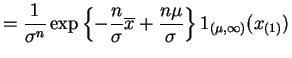 |
So, by the factorization criterion,
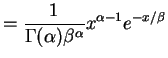 |
||
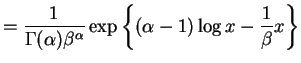 |
This is a two-parameter exponential family, so
- a.
- Done in class already.
- b.
-
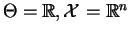 , and
, and
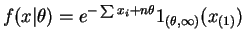
Suppose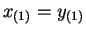 . Then
. Then
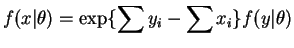
for all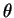 . So
. So
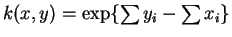 works.
works.
Suppose
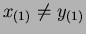 . Then for some
. Then for some 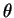 one of
one of
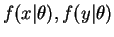 is zero and the other is not. So no
is zero and the other is not. So no
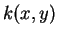 exists.
exists.
So
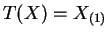 is minimal sufficient.
is minimal sufficient.
- c.
-
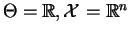 . The support does
not depend on
. The support does
not depend on 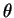 so we can work with ratios of densities.
The ratio of densities for two samples
so we can work with ratios of densities.
The ratio of densities for two samples 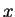 and
and 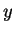 is
is
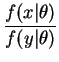
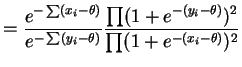
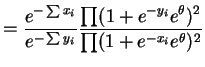
If the two samples contain identical values, i.e. if they have the same order statistics, then this ratio is constant in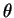 .
.
If the ratio is constant in
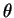 then the ratio of the two
product terms is constant. These terms are both polnomials of
degree
then the ratio of the two
product terms is constant. These terms are both polnomials of
degree 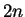 in
in
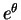 . If two polynomials are equal on an
open subset of the real line then they are equal on the entire
real line. Hence they have the same roots. The roots are
. If two polynomials are equal on an
open subset of the real line then they are equal on the entire
real line. Hence they have the same roots. The roots are
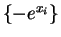 and
and
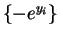 (each of degree 2). If
those sets are equal then the sets of sample values
(each of degree 2). If
those sets are equal then the sets of sample values 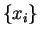 and
and
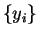 are equal, i.e. the two samples must have the same order
statistics.
are equal, i.e. the two samples must have the same order
statistics.
So the order statistics
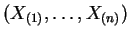 are minimal
sufficient.
are minimal
sufficient.
- d.
- Same idea:
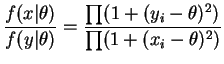
If the two samples have the same order statistics then the ratio is constant. If the ratio is constant for all real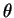 then
two polynomials in
then
two polynomials in 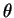 are equal on the complex plane, and so
the roots must be equal. The roots are the complex numbers
are equal on the complex plane, and so
the roots must be equal. The roots are the complex numbers
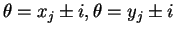
with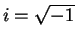 . So again the order statistics are minimal
sufficient.
. So again the order statistics are minimal
sufficient.
- e.
-
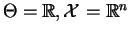 . The support does
not depend on
. The support does
not depend on 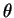 so we can work with ratios of densities.
The ratio of densities for two samples
so we can work with ratios of densities.
The ratio of densities for two samples 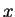 and
and 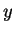 is
is
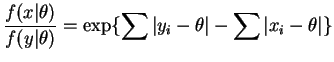
If the order statistics are the same then the ratio is constant. Suppose the order statistics differ. Then there is some open interval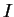 containing no
containing no 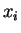 and no
and no 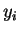 such that
such that
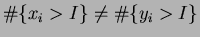 . The slopes on
. The slopes on 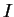 of
of
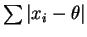 and
and
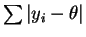 as functions of
as functions of
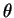 are
are
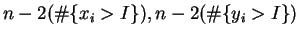
So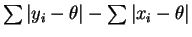 has slope
has slope
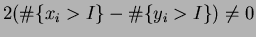
and so the ratio is not constant on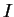 .
.
So again the order statistic is minimal sufficient.
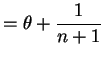 |
||
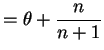 |
So
So
- a.
- The joint density of the data is
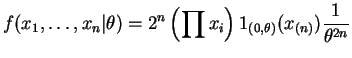
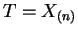 is sufficient (and minimal sufficient).
is sufficient (and minimal sufficient). 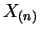 has
density
has
density
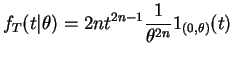
Thus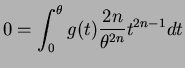
for all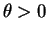 means
means
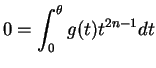
for almost all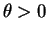 , and this in turn implies
, and this in turn implies
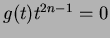 and hence
and hence 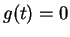 for all
for all 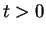 . So
. So
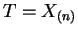 is complete.
is complete.
- b.
- Exponential family,
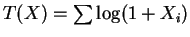 ,
,
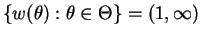
which is an open interval. - c.
- Exponential family,
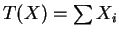 ,
,
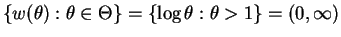
which is an open interval. - d.
- Exponential family,
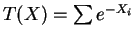 ,
,
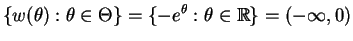
which is an open interval. - e.
- Exponential family,
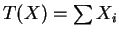 ,
,
![$\displaystyle \{w(\theta): \theta \in \Theta\} = \{\log \theta-\log(1-\theta): 0 \le \theta \le 1\} = [-\infty,\infty]$](img82.png)
which contains an open interval.
