- a.
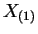 is sufficient.
is sufficient.
- b.
- The likelihood increases up to
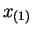 and then is zero.
So the MLE is
and then is zero.
So the MLE is
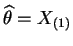 .
.
- c.
- The expected value of a single observation is
![$\displaystyle E_{\theta}[X] = \int_{\theta}^{\infty}x\theta\frac{1}{x^{2}}dx = \theta\int_{\theta}^{\infty}\frac{1}{x}dx = \infty$](img87.png)
So the (usual) method of moments estimator does not exist.
- a.
- The likelihood and log likelihood are
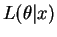
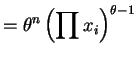
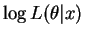
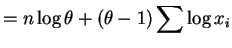
The derivative of the log likelihood and its unique root are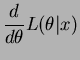
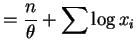
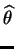
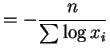
Since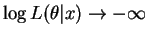 as
as
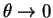 or
or
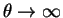 and the likelihood
is differentiable on the parameter space this root is a global
maximum.
and the likelihood
is differentiable on the parameter space this root is a global
maximum.
Now
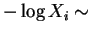 Exponential
Exponential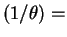 Gamma
Gamma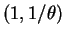 . So
. So
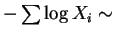 Gamma
Gamma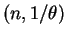 . So
. So
![$\displaystyle E\left[-\frac{n}{\sum \log X_{i}}\right]$](img104.png)
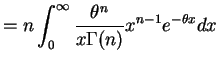
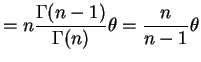
and![$\displaystyle E\left[\left(\frac{n}{\sum\log X_{i}}\right)^{2}\right] = n^{2}\frac{\Gamma(n-2)}{\Gamma(n)}\theta^{2} = \frac{n^{2}}{(n-1)(n-2)}\theta^{2}$](img107.png)
SoVar 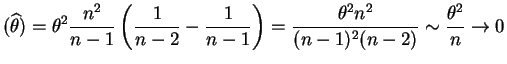
as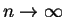 .
.
- b.
- The mean of a single observation is
![$\displaystyle E[X] = \int_{0}^{1}\theta x^{\theta} dx = \frac{\theta}{\theta+1}$](img110.png)
So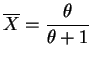
is the method of moments equation, and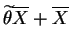
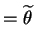
or 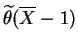
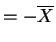
or 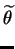
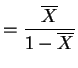
We could use the delta method to find a normal approximation to the distribution of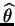 . The variance of the
approximate disrtibtion is larger than the variance of the MLE.
. The variance of the
approximate disrtibtion is larger than the variance of the MLE.
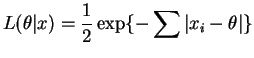 |
We know that the sample median
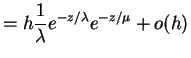 |
||
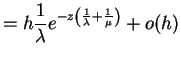 |
and, similarly,
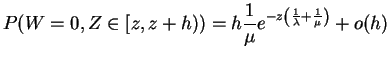 |
So
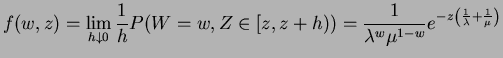 |
and therefore
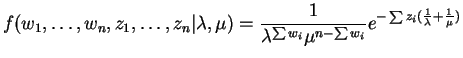 |
Since this factors,
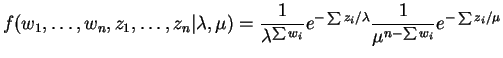 |
it is maximized by maximizing each term separately, which produces
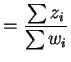 |
||
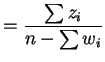 |
In words, if the
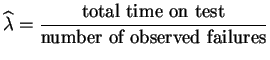 |
