General Issues
Make sure you name your files as requested, including matching the specified use of upper and lower case. This matters on file systems that are case-sensitive.
Make sure to commit your work to your local repository and push your commits to GitLab. We can only see what is on GitLab, not what is on your computer. You can check what we see by going to the GitLab web interface.
Include your name and the date in the header of your .Rmd file using author: and date: tags.
Your HTML file should be a report of your findings.
Any graph you show should be discussed in your narrative.
Any code you show should be discussed in your narrative.
If you do not need to discuss a piece of code in the narrative, use echo FALSE to avoid showing it.
1. New York City Airport Names
The names and airport codes for the three New York City airports in the nycflights13 data are shown in the following table:
library(dplyr)
##
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
##
## filter, lag
## The following objects are masked from 'package:base':
##
## intersect, setdiff, setequal, union
library(nycflights13)
nyc_faa <- unique(flights$origin)
tbl <- select(airports, faa, name) |> filter(faa %in% nyc_faa)
names(tbl) <- c("Code", "Name")
kbl <- knitr::kable(tbl, format = "html")
kableExtra::kable_styling(kbl, full_width = FALSE)
|
Code
|
Name
|
|
EWR
|
Newark Liberty Intl
|
|
JFK
|
John F Kennedy Intl
|
|
LGA
|
La Guardia
|
3. Air Time Distributions
Four possible visualizations without much fine tuning:
library(ggplot2)
library(ggridges)
library(patchwork)
thm <- theme_minimal() + theme(text = element_text(size = 16))
p0 <- ggplot(flights, aes(x = air_time)) + thm
p1 <- p0 +
geom_density(aes(color = origin), bw = 50) +
ggtitle("Color")
p2 <- p0 +
geom_density(aes(fill = origin), alpha = 0.4, bw = 50) +
ggtitle("Fill with Alpha Blending")
p3 <- p0 +
geom_density(bw = 50) + facet_wrap(~ origin, ncol = 1) +
ggtitle("Facets")
p4 <- p0 +
geom_density_ridges(aes(y = origin, height = after_stat(density)),
stat = "density", bw = 50) +
scale_y_discrete(limits = c("LGA", "JFK", "EWR")) +
ggtitle("Ridgeline")
(p1 | p2) / (p3 | p4)## + plot_layout(guides = "collect")
## Warning: Removed 9430 rows containing non-finite values (`stat_density()`).
## Removed 9430 rows containing non-finite values (`stat_density()`).
## Removed 9430 rows containing non-finite values (`stat_density()`).
## Removed 9430 rows containing non-finite values (`stat_density()`).
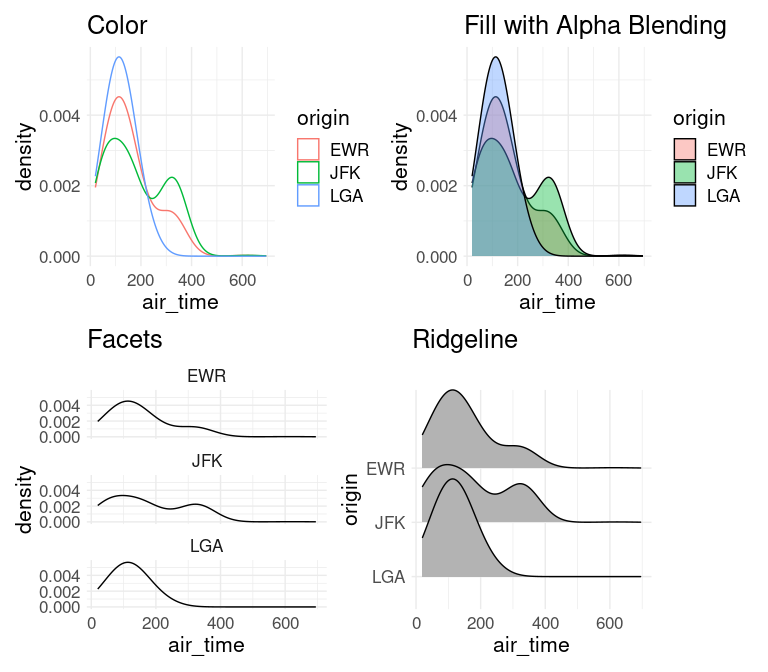
Neither single-plot view works particularly well in this case. For the plot using fill with alpha blending the overlap is too large to allow the densities to be distinguished easily. The plot mapping origin to color works somewhat better but the lines are still hard to follow. The faceted plot and the ridgeline plot are visually quite similar and both work fairly well.
Flights out of La Guardia are mostly shorter, with very few taking over 300 minutes. Somewhat more long flights originate from Newark, and considerably more long flights originate from JFK.
4. Highway Fuel Economy Over the Years, Revisited
library(readr)
if (! file.exists("vehicles.csv.zip"))
download.file("http://www.stat.uiowa.edu/~luke/data/vehicles.csv.zip",
"vehicles.csv.zip")
newmpg <- read_csv("vehicles.csv.zip", guess_max = 100000)
newmpg3 <- filter(newmpg, year <= 2023, year >= 2000) |>
mutate(year = factor(year))
All four approaches, with only minimal tuning for the three new ones:
alpha <- 0.2
size <- 0.3
p1 <- ggplot(newmpg3, aes(x = highway08, y = year)) +
geom_point(position = "jitter", size = size, alpha = alpha) +
ylab(NULL) +
thm
p2 <- ggplot(newmpg3, aes(y = highway08, x = year)) +
geom_boxplot() +
thm +
coord_flip()
p3 <- ggplot(newmpg3, aes(y = highway08, x = year)) +
geom_violin() +
thm +
coord_flip()
p4 <- ggplot(newmpg3, aes(x = highway08, y = year)) +
geom_density_ridges() +
thm
(p1 | p2) / (p3 | p4)
## Picking joint bandwidth of 1.22
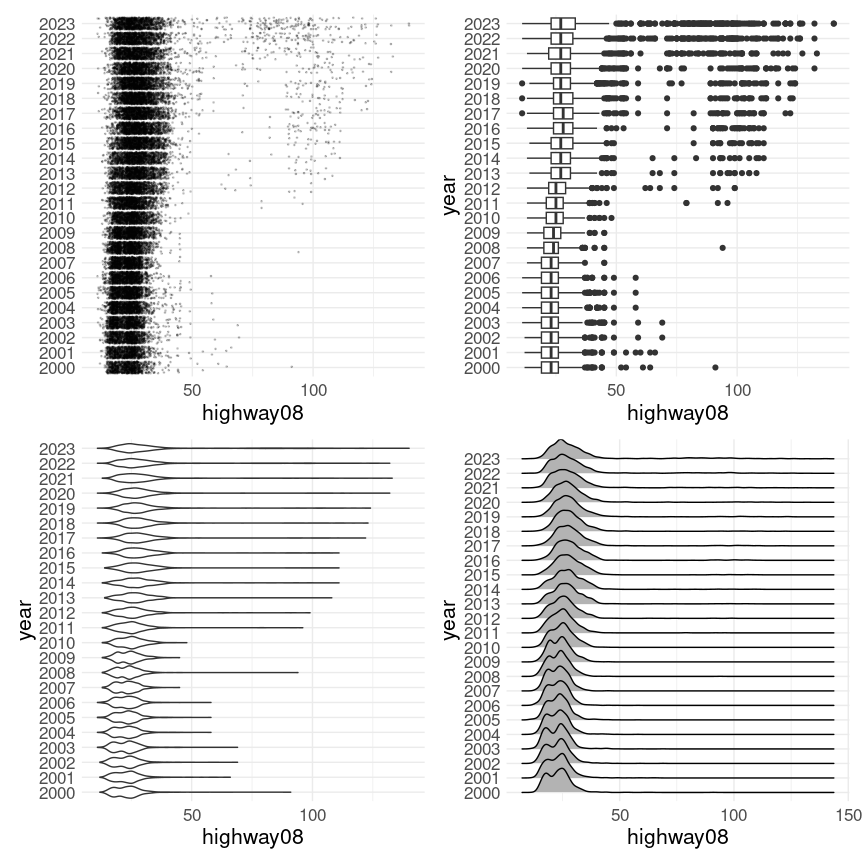
The three new approaches do a better job of conveying the increase in fuel economy for the bulk of the vehicles. Both violin and ridgeline plots show the slight bimodal structure in the early years; box plots cannot reflect this. Box plots put a high emphasis on the electric vehicles; this can be reduced by adjusting the point size used. Strip plots also allow the emerging electric vehicles to be seen. Violin plots and ridgeline plots do not show these very well as they are still too small a proportion of the total. The fact that violin plots stop at the maximum helps somewhat. The current geom_density_ridges implementation does not do this but could in principle be modified to do so.
LS0tCnRpdGxlOiAiQXNzaWdubWVudCA1IE5vdGVzIgpvdXRwdXQ6CiAgaHRtbF9kb2N1bWVudDoKICAgIHRvYzogeWVzCiAgICBjb2RlX2Rvd25sb2FkOiB0cnVlCiAgICBjb2RlX2ZvbGRpbmc6ICJoaWRlIgotLS0KCmBgYHtyIGdsb2JhbF9vcHRpb25zLCBpbmNsdWRlID0gRkFMU0V9CmtuaXRyOjpvcHRzX2NodW5rJHNldChjb2xsYXBzZSA9IFRSVUUpCmBgYAoKIyMgR2VuZXJhbCBJc3N1ZXMKCiogTWFrZSBzdXJlIHlvdSBuYW1lIHlvdXIgZmlsZXMgYXMgcmVxdWVzdGVkLCBpbmNsdWRpbmcgbWF0Y2hpbmcgdGhlCiAgc3BlY2lmaWVkIHVzZSBvZiB1cHBlciBhbmQgbG93ZXIgY2FzZS4gVGhpcyBtYXR0ZXJzIG9uIGZpbGUgc3lzdGVtcwogIHRoYXQgYXJlIGNhc2Utc2Vuc2l0aXZlLgoKKiBNYWtlIHN1cmUgdG8gY29tbWl0IHlvdXIgd29yayB0byB5b3VyIGxvY2FsIHJlcG9zaXRvcnkgYW5kIHB1c2ggeW91cgogIGNvbW1pdHMgdG8gR2l0TGFiLiBXZSBjYW4gb25seSBzZWUgd2hhdCBpcyBvbiBHaXRMYWIsIG5vdCB3aGF0IGlzIG9uCiAgeW91ciBjb21wdXRlci4gWW91IGNhbiBjaGVjayB3aGF0IHdlIHNlZSBieSBnb2luZyB0byB0aGUgR2l0TGFiIHdlYgogIGludGVyZmFjZS4KIAoqIEluY2x1ZGUgeW91ciBuYW1lIGFuZCB0aGUgZGF0ZSBpbiB0aGUgaGVhZGVyIG9mIHlvdXIgYC5SbWRgIGZpbGUKICB1c2luZyBgYXV0aG9yOmAgYW5kIGBkYXRlOmAgdGFncy4KCiogWW91ciBIVE1MIGZpbGUgc2hvdWxkIGJlIGEgcmVwb3J0IG9mIHlvdXIgZmluZGluZ3MuCgogICAgKiBBbnkgZ3JhcGggeW91IHNob3cgc2hvdWxkIGJlIGRpc2N1c3NlZCBpbiB5b3VyIG5hcnJhdGl2ZS4KCiAgICAqIEFueSBjb2RlIHlvdSBzaG93IHNob3VsZCBiZSBkaXNjdXNzZWQgaW4geW91ciBuYXJyYXRpdmUuCgogICAgKiBJZiB5b3UgZG8gbm90IG5lZWQgdG8gZGlzY3VzcyBhIHBpZWNlIG9mIGNvZGUgaW4gdGhlIG5hcnJhdGl2ZSwKICAgICAgdXNlIGBlY2hvIEZBTFNFYCB0byBhdm9pZCBzaG93aW5nIGl0LgoKCiMjIDEuIE5ldyBZb3JrIENpdHkgQWlycG9ydCBOYW1lcwoKVGhlIG5hbWVzIGFuZCBhaXJwb3J0IGNvZGVzIGZvciB0aGUgdGhyZWUgTmV3IFlvcmsgQ2l0eSBhaXJwb3J0cyBpbgp0aGUgYG55Y2ZsaWdodHMxM2AgZGF0YSBhcmUgc2hvd24gaW4gdGhlIGZvbGxvd2luZyB0YWJsZToKCmBgYHtyfQpsaWJyYXJ5KGRwbHlyKQpsaWJyYXJ5KG55Y2ZsaWdodHMxMykKbnljX2ZhYSA8LSB1bmlxdWUoZmxpZ2h0cyRvcmlnaW4pCnRibCA8LSBzZWxlY3QoYWlycG9ydHMsIGZhYSwgbmFtZSkgfD4gZmlsdGVyKGZhYSAlaW4lIG55Y19mYWEpCm5hbWVzKHRibCkgPC0gYygiQ29kZSIsICJOYW1lIikKa2JsIDwtIGtuaXRyOjprYWJsZSh0YmwsIGZvcm1hdCA9ICJodG1sIikKa2FibGVFeHRyYTo6a2FibGVfc3R5bGluZyhrYmwsIGZ1bGxfd2lkdGggPSBGQUxTRSkKYGBgCgoKIyMgMi4gQXZlcmFnZSBhbmQgTWVkaWFuIERlcGFydHVyZSBEZWxheXMKCmBgYHtyfQp0YmwgPC0KICAgIGdyb3VwX2J5KGZsaWdodHMsIG9yaWdpbikgfD4KICAgIHN1bW1hcml6ZShhdmdfZGVwX2RlbGF5ID0gbWVhbihkZXBfZGVsYXksIG5hLnJtID0gVFJVRSksCiAgICAgICAgICAgICAgbWVkX2RlcF9kZWxheSA9IG1lZGlhbihkZXBfZGVsYXksIG5hLnJtID0gVFJVRSkpIHw+CiAgICB1bmdyb3VwKCkKbmFtZXModGJsKSA8LSBjKCJPcmlnaW4iLCAiQXZlcmFnZSBEZWxheSIsICJNZWRpYW4gRGVsYXkiKQprYmwgPC0ga25pdHI6OmthYmxlKHRibCwgZm9ybWF0ID0gImh0bWwiLCBkaWdpdHMgPSAxKQprYWJsZUV4dHJhOjprYWJsZV9zdHlsaW5nKGtibCwgZnVsbF93aWR0aCA9IEZBTFNFKQpgYGAKCkFpcmxpbmVzIHdvcmsgdmVyeSBoYXJkIHRvIGhhdmUgZmxpZ2h0cyBsZWF2ZSBvbiB0aW1lLiBJbiBmYWN0IHRoZQptYWpvcml0eSBhdCBhbGwgdGhyZWUgYWlycG9ydHMgbGVmdCBlYXJseSBhbmQgc28gdGhlIG1lZGlhbiBkZWxheXMgYXJlCm5lZ2F0aXZlLiBCdXQgdGhlIGRpc3RyaWJ1dGlvbnMgb2YgZGVsYXkgdGltZXMgYXJlIGhlYXZpbHkgc2tld2VkIHRvCnRoZSByaWdodCwgc28gdGhlIGF2ZXJhZ2UgZGVwYXJ0dXJlIGRlbGF5cyBhcmUgcXVpdGUgYSBiaXQgbGFyZ2VyLgoKCiMjIDMuIEFpciBUaW1lIERpc3RyaWJ1dGlvbnMKCkZvdXIgcG9zc2libGUgdmlzdWFsaXphdGlvbnMgd2l0aG91dCBtdWNoIGZpbmUgdHVuaW5nOgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGZpZy5oZWlnaHQgPSA3fQpsaWJyYXJ5KGdncGxvdDIpCmxpYnJhcnkoZ2dyaWRnZXMpCmxpYnJhcnkocGF0Y2h3b3JrKQp0aG0gPC0gdGhlbWVfbWluaW1hbCgpICsgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTYpKQpwMCA8LSBnZ3Bsb3QoZmxpZ2h0cywgYWVzKHggPSBhaXJfdGltZSkpICsgdGhtCnAxIDwtIHAwICsKICAgIGdlb21fZGVuc2l0eShhZXMoY29sb3IgPSBvcmlnaW4pLCBidyA9IDUwKSArCiAgICBnZ3RpdGxlKCJDb2xvciIpCnAyIDwtIHAwICsKICAgIGdlb21fZGVuc2l0eShhZXMoZmlsbCA9IG9yaWdpbiksIGFscGhhID0gMC40LCBidyA9IDUwKSArCiAgICBnZ3RpdGxlKCJGaWxsIHdpdGggQWxwaGEgQmxlbmRpbmciKQpwMyA8LSBwMCArCiAgICBnZW9tX2RlbnNpdHkoYncgPSA1MCkgKyBmYWNldF93cmFwKH4gb3JpZ2luLCBuY29sID0gMSkgKwogICAgZ2d0aXRsZSgiRmFjZXRzIikKcDQgPC0gcDAgKwogICAgZ2VvbV9kZW5zaXR5X3JpZGdlcyhhZXMoeSA9IG9yaWdpbiwgaGVpZ2h0ID0gYWZ0ZXJfc3RhdChkZW5zaXR5KSksCiAgICAgICAgICAgICAgICAgICAgICAgIHN0YXQgPSAiZGVuc2l0eSIsIGJ3ID0gNTApICsKICAgIHNjYWxlX3lfZGlzY3JldGUobGltaXRzID0gYygiTEdBIiwgIkpGSyIsICJFV1IiKSkgKwogICAgZ2d0aXRsZSgiUmlkZ2VsaW5lIikKKHAxIHwgcDIpIC8gKHAzIHwgcDQpIyMgKyBwbG90X2xheW91dChndWlkZXMgPSAiY29sbGVjdCIpCmBgYAoKTmVpdGhlciBzaW5nbGUtcGxvdCB2aWV3IHdvcmtzIHBhcnRpY3VsYXJseSB3ZWxsIGluIHRoaXMgY2FzZS4gIEZvcgp0aGUgcGxvdCB1c2luZyBgZmlsbGAgd2l0aCBgYWxwaGFgIGJsZW5kaW5nIHRoZSBvdmVybGFwIGlzIHRvbyBsYXJnZQp0byBhbGxvdyB0aGUgZGVuc2l0aWVzIHRvIGJlIGRpc3Rpbmd1aXNoZWQgZWFzaWx5LiBUaGUgcGxvdCBtYXBwaW5nCmBvcmlnaW5gIHRvIGBjb2xvcmAgd29ya3Mgc29tZXdoYXQgYmV0dGVyIGJ1dCB0aGUgbGluZXMgYXJlIHN0aWxsCmhhcmQgdG8gZm9sbG93LiBUaGUgZmFjZXRlZCBwbG90IGFuZCB0aGUgcmlkZ2VsaW5lIHBsb3QgYXJlIHZpc3VhbGx5CnF1aXRlIHNpbWlsYXIgYW5kIGJvdGggd29yayBmYWlybHkgd2VsbC4KCkZsaWdodHMgb3V0IG9mIExhIEd1YXJkaWEgYXJlIG1vc3RseSBzaG9ydGVyLCB3aXRoIHZlcnkgZmV3IHRha2luZwpvdmVyIDMwMCBtaW51dGVzLiBTb21ld2hhdCBtb3JlIGxvbmcgZmxpZ2h0cyBvcmlnaW5hdGUgZnJvbSBOZXdhcmssCmFuZCBjb25zaWRlcmFibHkgbW9yZSBsb25nIGZsaWdodHMgb3JpZ2luYXRlIGZyb20gSkZLLgoKCiMjIDQuIEhpZ2h3YXkgRnVlbCBFY29ub215IE92ZXIgdGhlIFllYXJzLCBSZXZpc2l0ZWQKCmBgYHtyLCBtZXNzYWdlID0gRkFMU0V9CmxpYnJhcnkocmVhZHIpCmlmICghIGZpbGUuZXhpc3RzKCJ2ZWhpY2xlcy5jc3YuemlwIikpCiAgICBkb3dubG9hZC5maWxlKCJodHRwOi8vd3d3LnN0YXQudWlvd2EuZWR1L35sdWtlL2RhdGEvdmVoaWNsZXMuY3N2LnppcCIsCiAgICAgICAgICAgICAgICAgICJ2ZWhpY2xlcy5jc3YuemlwIikKbmV3bXBnIDwtIHJlYWRfY3N2KCJ2ZWhpY2xlcy5jc3YuemlwIiwgZ3Vlc3NfbWF4ID0gMTAwMDAwKQpuZXdtcGczIDwtIGZpbHRlcihuZXdtcGcsIHllYXIgPD0gMjAyMywgeWVhciA+PSAyMDAwKSB8PgogICAgbXV0YXRlKHllYXIgPSBmYWN0b3IoeWVhcikpCmBgYAoKQWxsIGZvdXIgYXBwcm9hY2hlcywgd2l0aCBvbmx5IG1pbmltYWwgdHVuaW5nIGZvciB0aGUgdGhyZWUgbmV3IG9uZXM6CgpgYGB7ciwgZmlnLmhlaWdodCA9IDksIGZpZy53aWR0aCA9IDl9CmFscGhhIDwtIDAuMgpzaXplIDwtIDAuMwpwMSA8LSBnZ3Bsb3QobmV3bXBnMywgYWVzKHggPSBoaWdod2F5MDgsIHkgPSB5ZWFyKSkgKwogICAgZ2VvbV9wb2ludChwb3NpdGlvbiA9ICJqaXR0ZXIiLCBzaXplID0gc2l6ZSwgYWxwaGEgPSBhbHBoYSkgKwogICAgeWxhYihOVUxMKSArCiAgICB0aG0KcDIgPC0gZ2dwbG90KG5ld21wZzMsIGFlcyh5ID0gaGlnaHdheTA4LCB4ID0geWVhcikpICsKICAgIGdlb21fYm94cGxvdCgpICsKICAgIHRobSArCiAgICBjb29yZF9mbGlwKCkKcDMgPC0gZ2dwbG90KG5ld21wZzMsIGFlcyh5ID0gaGlnaHdheTA4LCB4ID0geWVhcikpICsKICAgIGdlb21fdmlvbGluKCkgKwogICAgdGhtICsKICAgIGNvb3JkX2ZsaXAoKQpwNCA8LSBnZ3Bsb3QobmV3bXBnMywgYWVzKHggPSBoaWdod2F5MDgsIHkgPSB5ZWFyKSkgKwogICAgZ2VvbV9kZW5zaXR5X3JpZGdlcygpICsKICAgIHRobQoKKHAxIHwgcDIpIC8gKHAzIHwgcDQpCmBgYAoKVGhlIHRocmVlIG5ldyBhcHByb2FjaGVzIGRvIGEgYmV0dGVyIGpvYiBvZiBjb252ZXlpbmcgdGhlIGluY3JlYXNlIGluCmZ1ZWwgZWNvbm9teSBmb3IgdGhlIGJ1bGsgb2YgdGhlIHZlaGljbGVzLiBCb3RoIHZpb2xpbiBhbmQgcmlkZ2VsaW5lCnBsb3RzIHNob3cgdGhlIHNsaWdodCBiaW1vZGFsIHN0cnVjdHVyZSBpbiB0aGUgZWFybHkgeWVhcnM7IGJveCBwbG90cwpjYW5ub3QgcmVmbGVjdCB0aGlzLiBCb3ggcGxvdHMgcHV0IGEgaGlnaCBlbXBoYXNpcyBvbiB0aGUgZWxlY3RyaWMKdmVoaWNsZXM7IHRoaXMgY2FuIGJlIHJlZHVjZWQgYnkgYWRqdXN0aW5nIHRoZSBwb2ludCBzaXplIHVzZWQuICBTdHJpcApwbG90cyBhbHNvIGFsbG93IHRoZSBlbWVyZ2luZyBlbGVjdHJpYyB2ZWhpY2xlcyB0byBiZSBzZWVuLiAgVmlvbGluCnBsb3RzIGFuZCByaWRnZWxpbmUgcGxvdHMgZG8gbm90IHNob3cgdGhlc2UgdmVyeSB3ZWxsIGFzIHRoZXkgYXJlCnN0aWxsIHRvbyBzbWFsbCBhIHByb3BvcnRpb24gb2YgdGhlIHRvdGFsLiBUaGUgZmFjdCB0aGF0IHZpb2xpbiBwbG90cwpzdG9wIGF0IHRoZSBtYXhpbXVtIGhlbHBzIHNvbWV3aGF0LiBUaGUgY3VycmVudCBgZ2VvbV9kZW5zaXR5X3JpZGdlc2AKaW1wbGVtZW50YXRpb24gZG9lcyBub3QgZG8gdGhpcyBidXQgY291bGQgaW4gcHJpbmNpcGxlIGJlIG1vZGlmaWVkIHRvCmRvIHNvLgo=


