Visualization and Comparison
A visualization of a single value without some comparative context is rarely useful
Useful visualizations almost always involve comparisons.
position of a value on an axis
relative position of two values
relative magnitudes of two values
A simple and common setting: Visualizing a measurement or summary for each of a set of categories.
Some of the more common visualizations:
Some less frequently used visualizations:
Waterfall Charts
Polar Area Charts (Coxcomb Charts)
Dumbbell Charts
Some questions to keep in mind:
Dot Plots
Basics
One of the simplest visualizations of a single numerical variable with a modest number of observations and labels for the observations is a dot plot , or Cleveland dot plot :
library(dplyr)
library(ggplot2)
library(gapminder)
le_am_2007 <- filter(gapminder,
year == 2007,
continent == "Americas")
thm <- theme_minimal() +
theme(text = element_text(size = 16))
ggplot(le_am_2007,
aes(y = country, x = lifeExp)) +
geom_point(color = "deepskyblue3",
size = 2) +
labs(x = "Life Expectancy (years)",
y = NULL) +
thm
This visualization
shows the overall distribution of the data, and
makes it easy to locate the life expectancy of a particular country.
Unless there is a natural order to the categories (e.g. months of the year or days of the week) it is usually better to reorder to make the plot increasing or decreasing:
ggplot(le_am_2007,
aes(y = reorder(country, lifeExp),
x = lifeExp)) +
geom_point(color = "deepskyblue3",
size = 2) +
labs(x = "Life Expectancy (years)",
y = NULL) +
thm
Locating a particular country is a little more difficult.
But the shape of the distribution is more apparent.
Approximate median and quartiles can be read off easily.
Dot plots are particularly appropriate for interval data.
Dot plots are often very useful for group summaries like totals or averages.
For the barley data, total yield within each site, adding up across all varieties and both years, can be computed as
b_tot_site <-
group_by(barley, site) |>
summarize(yield = sum(yield))The totals can then be visualized in a dot plot:
ggplot(b_tot_site, aes(x = yield, y = site)) +
geom_point(color = "deepskyblue3", size = 2.5) +
labs(x = "Total Yield (bushels/acre)", y = NULL) +
thm
Larger Data Sets
For larger data sets, like the citytemps data with 141 observations, over-plotting of labels becomes a problem:
ggplot(citytemps,
aes(x = temp, y = reorder(city, temp))) +
geom_point(color = "deepskyblue3", size = 0.5) +
labs(x = "Temperature (degrees F)", y = NULL) +
thm
Reducing to 30 or 40, e.g. by taking a sample or a meaningful subset, can help:
ct1 <- filter(citytemps, temp < 32) |> sample_n(10)
ct2 <- filter(citytemps, temp >= 32) |> sample_n(20)
ctsamp <- bind_rows(ct1, ct2)
ggplot(ctsamp,
aes(x = temp, y = reorder(city, temp))) +
geom_point(color = "deepskyblue3", size = 2) +
labs(x = "Temperature (degrees F)", y = NULL) +
thm
Some Variations
The size of the dots can be used to encode an additional numeric variable.
This view uses area to encode population size:
ggplot(le_am_2007, aes(y = reorder(country, lifeExp),
x = lifeExp,
size = pop / 1000000)) +
geom_point(col = "deepskyblue3") +
labs(x = "Life Expectancy (years)", y = NULL) +
scale_size_area("Population\n(Millions)",
max_size = 8) +
thm + theme(legend.position = "top")
This is sometimes called a bubble chart .
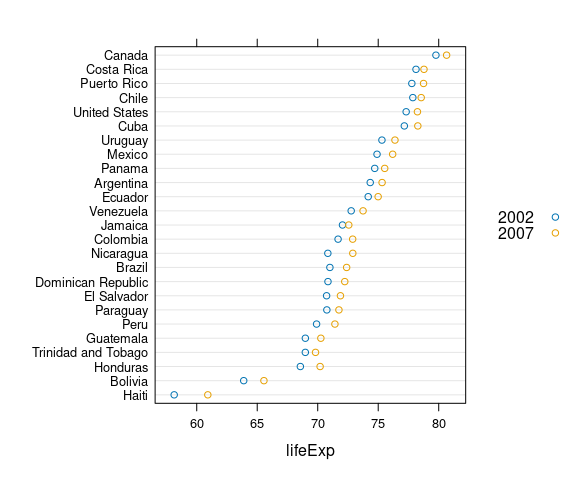
Repeated measures, such as values for 2002 and 2007, can be shown and distinguished by color, shape, or both.
Using color:
## filter down to data for 2002 and 2007
## for the Americas
le2 <- filter(gapminder,
year >= 2002,
continent == "Americas")
## make a factor Year to get a discrete color
## palette, not a continuous one
le2 <- mutate(le2, Year = factor(year))
ggplot(le2, aes(y = reorder(country, lifeExp),
x = lifeExp,
color = Year)) +
geom_point() +
labs(x = "Life Expectancy (years)", y = NULL) +
thm + theme(legend.position = "top")Using shape for the barley data:
b_tot <-
group_by(barley, site, year) |>
summarize(yield = sum(yield), .groups = "drop")
ggplot(b_tot, aes(x = yield, y = site, shape = year)) +
geom_point(color = "deepskyblue3", size = 3) +
labs(x = "Total Yield (bushels/acre)", y = NULL) +
thm + theme(legend.position = "top")
For repeated two values per class it can help to connect the two dots.
This visually emphasizes the relative sizes of differences.
The result is sometimes called a dumbbell chart .
For the barley yields data:
ggplot(b_tot, aes(x = yield, y = site)) +
geom_line(aes(group = site),
linewidth = 2,
color = "grey") +
geom_point(aes(color = year), size = 4) +
labs(x = "Total Yield (bushels/acre)", y = NULL) +
thm + theme(legend.position = "top")
For the Gapminder life expectancy data:
ggplot(le2, aes(y = reorder(country, lifeExp),
x = lifeExp,
color = Year)) +
geom_line(aes(group = country),
linewidth = 1.5,
color = "grey") +
geom_point(size = 2.5) +
labs(x = "Life Expectancy (years)", y = NULL) +
thm + theme(legend.position = "top")
Variations in Appearance
The dot plots introduced by W. S. Cleveland in his 1993 book Visualizing Data use only horizontal grid lines.
This also corresponds to the dot plots provided by base and lattice graphics and to the dot plot obtained using the Wall Street Journal theme from the ggthemespackage:
ggplot(b_tot_site, aes(x = yield, y = site)) +
geom_point(size = 2) +
labs(x = "Total Yield (bushels/acre)", y = NULL) +
ggthemes::theme_wsj()
A theme to closely match the style used by Cleveland can be defined as
theme_dotplotx <- function() {
theme(
## remove the vertical grid lines
panel.grid.major.x = element_blank(),
panel.grid.minor.x = element_blank(),
## explicitly set the horizontal lines
## (or they will disappear too)
panel.grid.major.y =
element_line(color = "black",
linetype = 3),
axis.text.y = element_text(size = rel(1.2)),
## use a white backgrounsd
panel.background =
element_rect(fill = "white",
color = NA),
panel.border =
element_rect(fill = NA,
color = "grey20"),
## increase text size
text = element_text(size = 16))
}This produces
ggplot(b_tot_site, aes(x = yield, y = site)) +
geom_point(size = 2) +
labs(x = "Total Yield (bushels/acre)",
y = NULL) +
theme_dotplotx()
Bar Charts
Basics
A basic bar chart:
p <- ggplot(le_am_2007) +
geom_col(aes(y = lifeExp,
x = reorder(country, lifeExp)),
fill = "deepskyblue3") +
labs(y = "Life Expectancy (years)",
x = NULL) +
scale_y_continuous(
expand = expansion(mult = c(0, .1))) +
thm
p
The labels are a mess.
One option is to write labels at an angle, but this makes them hard to read.
Flipping the plot is usually a better option.
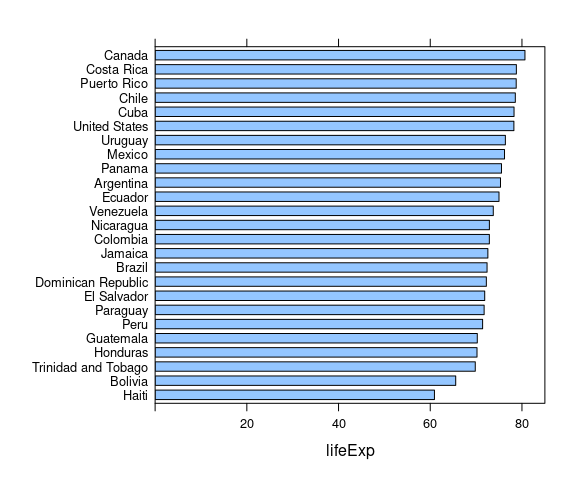
To make labels readable we can flip the plot:
## Redoing the plot plot with `x` and `y` aesthetics
## reversed did not work in the past but does work in
## current ggplot2 versions.
## But coord_flip() is still sometimes necessary.
p + coord_flip()
Some Notes
Bar charts seem to be used much more than dot plots in the popular media, but they are less widely applicable.
Research on visual perception has shown that viewers of bar charts subconsciously, or pre-attentively , focus on relative lengths of bars.
This means that for a bar chart to be appropriate and work well:
This in turn implies that bar charts should always have a zero base line.
You may need to intervene with your software’s defaults to make this happen.
Creating a bar chart with a non-zero base line is possible in ggplot but not easy:
baseline <- 60
ticks <- c(0, 10, 20, 30)
ggplot(le_am_2007,
aes(x = lifeExp - baseline,
y = reorder(country, lifeExp))) +
geom_col(fill = "deepskyblue3") +
labs(x = "Life Expectancy (years)",
y = NULL) +
scale_x_continuous(
breaks = ticks,
labels = ticks + baseline,
expand = expansion(mult = c(0, .1))) +
thm + labs(title = "A Bad Bar Chart")
Bar charts always push the viewer to ratio comparisons, whether they are meaningful or not.
Using a non-zero baseline can therefore mislead the viewer .
Some news organizations seem particularly prone to taking advantage of/falling prey to this issue.
A blog post discusses a court case in New Zealand about a misleading bar chart with a non-zero baseline.
Another blog post may also be helpful.
The art of making simple things harder (February 2, 2024):
Defense against dishonest charts (February 13, 2025).
Data With Both Positive and Negative Values
Bar charts can be used for data containing both positive and negative values:
ctsampC <- mutate(ctsamp, temp = round((temp - 32) / 1.8))
p1 <- ggplot(ctsampC, aes(y = city, x = temp)) +
geom_point(color = "deepskyblue3") +
geom_vline(xintercept = 0, lty = 2) +
labs(x = "Temperature (degrees C)", y = NULL) +
thm
p2 <- ggplot(ctsampC, aes(x = temp, y = city)) +
geom_col(fill = "deepskyblue3") +
labs(x = "Temperature (degrees C)", y = NULL) +
thm
library(patchwork)
p1 + p2
This puts a strong emphasis on the base line
This can be useful if the baseline is meaningful, such as
Zero degrees Fahrenheit is not meaningful:
p1 <- ggplot(ctsamp, aes(y = city, x = temp)) +
geom_point(color = "deepskyblue3") +
geom_vline(xintercept = 0, lty = 2) +
labs(x = "Temperature (degrees F)", y = NULL) +
thm
p2 <- ggplot(ctsamp, aes(x = temp, y = city)) +
geom_col(fill = "deepskyblue3") +
labs(x = "Temperature (degrees F)", y = NULL) +
thm
p1 + p2
Grouped Bar Charts
A grouped bar chart can be used to show two measurements, e.g. life expectancy values for two years.
ggplot(le2) +
geom_col(aes(x = lifeExp,
y = reorder(country, lifeExp),
fill = Year),
position = "dodge") +
labs(x = "Life Expectancy (years)",
y = NULL) +
scale_x_continuous(
expand = expansion(mult = c(0, .1))) +
thm
This visualization would be more effective for
In this case the dot plot is a much better choice.
For the barley data, looking at total yields for each of the sites and the two years:
ggplot(b_tot) +
geom_col(aes(x = yield, y = site, fill = year),
position = "dodge") +
labs(x = "Total Yield (bushels/acre)",
y = NULL) +
scale_x_continuous(
expand = expansion(mult = c(0, .1))) +
thm
Stacked Bar Charts
A stacked bar chart is appropriate when adding the values within a category to form a total makes sense.
For the barley data:
ggplot(b_tot) +
geom_col(aes(x = yield, y = site, fill = year),
position = "stack") +
labs(x = "Total Yield (bushels/acre)",
y = NULL) +
scale_x_continuous(
expand = expansion(mult = c(0, .1))) +
thm
The combined bars show the two-year totals.
The bar segments show the contribution of each year within the sites.
Comparing 1931 yields across sites is easy; comparing 1932 values is harder.
A stacked bar chart would make no sense for the two-year life expectancy data.
Category Order
Ordering of categories can change the visual effectiveness of bar charts.
Supermarket Sales
A small data set on multi-national supermarket chain sales:
chains <- read.csv(textConnection("Chain, Total, Foreign
Walmart, 22, 5
Costco, 4.5, 2
Tesco, 3, 0.5
Carrefour, 2.5, 2"))
chains <- mutate(chains, Home = Total - Foreign)
tbl <- select(chains, Chain, Home, Foreign, Total)
kbl <- knitr::kable(tbl, format = "html")
kableExtra::kable_styling(kbl, full_width = FALSE)
Chain
Home
Foreign
Total
Walmart
17.0
5.0
22.0
Costco
2.5
2.0
4.5
Tesco
2.5
0.5
3.0
Carrefour
0.5
2.0
2.5
The default alphabetical ordering of the chains in a bar chart is not ideal:
library(tidyr)
chains <- mutate(chains, Total = NULL)
lchains <- pivot_longer(chains,
-Chain,
names_to = "Type",
values_to = "Sales")
p <- ggplot(lchains,
aes(x = Sales, y = Chain, fill = Type)) +
geom_col() +
ylab(NULL) +
scale_x_continuous(
expand = expansion(mult = c(0, .1))) +
scale_fill_brewer(
palette = "Paired",
guide = guide_legend(title = NULL,
reverse = TRUE)) +
thm + theme(legend.position = "top")
p
Reordering by total sales produces a better result:
lchain_s <-
mutate(lchains,
Chain = reorder(Chain, Sales, FUN = sum))
p %+% lchain_s
With this ordering, comparing the first category of sales, Home, among chains is easier than comparing the Foreign sales as the Home values have a common baseline.
If the goal of the visualization is to emphasize the foreign sales then reversing the order would be better.
lchain_st <-
mutate(lchain_s,
Type = factor(Type,
levels = c("Home", "Foreign")))
p %+% lchain_st +
scale_fill_brewer(palette = "Paired",
guide = guide_legend(title = NULL,
reverse = TRUE),
direction = -1)
This also makes it easy to see that Walmart’s international sales alone exceed the total sales of each of the other chains.
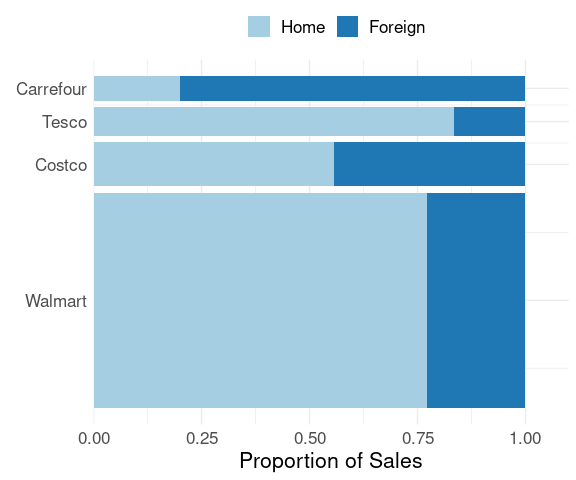
A filled bar chart can be used to help compare the proportions of total sales from foreign stores.
levs <-
levels(with(chains,
reorder(Chain, Foreign / (Foreign + Home))))
mutate(lchain_st, Chain = factor(Chain, levs)) |>
ggplot(aes(x = Sales, y = Chain, fill = Type)) +
geom_col(position = "fill") +
labs(x = "Proportion of Sales", y = NULL) +
scale_x_continuous(
expand = expansion(mult = c(0, .1))) +
scale_fill_brewer(palette = "Paired",
guide = guide_legend(title = NULL,
reverse = TRUE),
direction = -1) +
thm + theme(legend.position = "top")
A spine plot shows the total sales by mapping them to the bar widths:
## geom_col() does not allow `width` to be used as an aesthetic,
## but a spine plot can be produced by calculating bar positions
## and widths. This requires creating a vertical bar chart and
## using coord_flip().
gap <- 0.02
spchains <-
mutate(chains,
Total = Home + Foreign,
tot.prp = Total / sum(Total), ## bar widths
start = c(0, cumsum(tot.prp + gap)[-n()]),
end = tot.prp[1] + c(0, cumsum(tot.prp[-1] + gap)),
mid = (start + end) / 2) ## bar positions
lspchains <- pivot_longer(spchains,
c(Home, Foreign),
names_to = "Type",
values_to = "Sales") |>
mutate(Chain = reorder(Chain, Total))
X <- unique(lspchains$mid) ## axis breaks
C <- unique(lspchains$Chain) ## axis break labels
W <- lspchains$tot.prp
ggplot(lspchains, aes(x = mid, y = Sales, fill = Type)) +
geom_col(position = "fill", width = W) +
scale_x_continuous(breaks = X, labels = C) +
labs(x = element_blank(), y = "Proportion of Sales") +
scale_y_continuous(
expand = expansion(mult = c(0, .1))) +
scale_fill_brewer(palette = "Paired",
guide = guide_legend(title = NULL,
reverse = TRUE),
direction = -1) +
thm + theme(legend.position = "top") +
coord_flip()
2016 Election Results
Another example for filled bar charts is provided by 2016 presidential election results by state.
This is produced by default settings.
The values for Clinton are easy to compare, as they are on a common baseline.
The values for Other are also on a common baseline, but the numbers for Trump are not.
p <- ggplot(geofacet::election,
aes(x = votes,
y = state,
fill = candidate)) +
geom_col(position = "fill") +
scale_x_continuous(expand = c(0, 0)) +
xlab(NULL) +
geom_vline(xintercept = 0.5, linetype = 2)
p
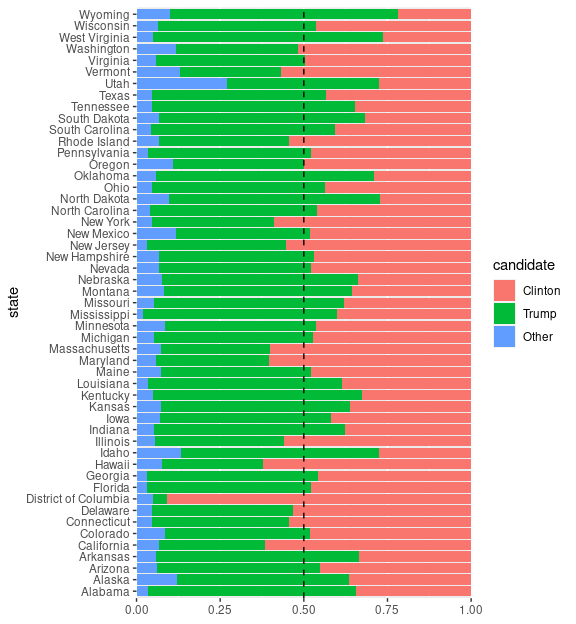
Reordering the categories puts both Clinton and Trump on common baselines and also matches the common color use:
## move 'Other' to middle, align Clinton/Trump with colors
elect <-
mutate(geofacet::election,
candidate = factor(candidate,
c("Trump", "Other", "Clinton")))
p %+% elect
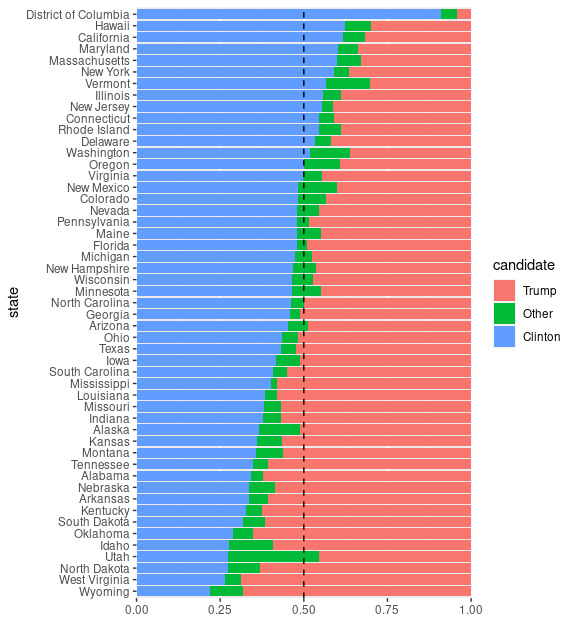
Different orderings of the states can be used to achieve different goals.
Ordering by Clinton’s percentage makes it easier to see where she had an outright majority.
elect_wide <- pivot_wider(select(elect, -votes),
names_from = candidate,
values_from = pct)
## ordered by Clinton pct
slevs <- arrange(elect_wide, Clinton) |>
pull(state)
p %+% mutate(elect, state = factor(state, slevs))
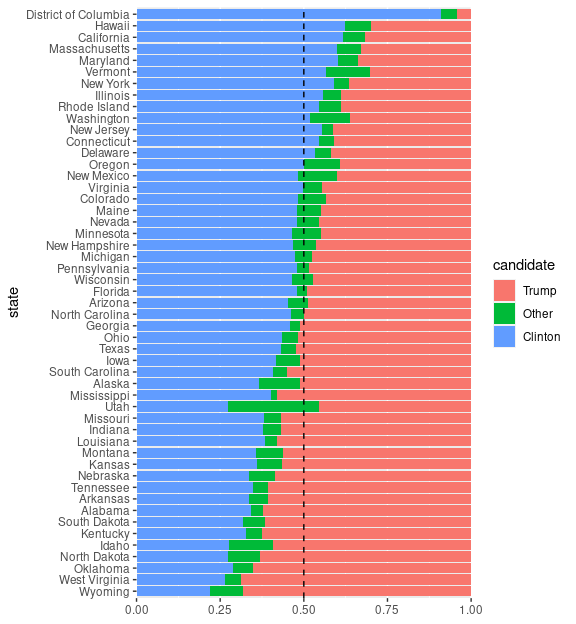
Another possibility is to order by winning margin between the two major candidates.
## ordered by winning margin
slevs <- arrange(elect_wide, Clinton - Trump) |>
pull(state)
p %+% mutate(elect, state = factor(state, slevs))
Faceting
Faceting can be used with dot plots and bar charts as well:
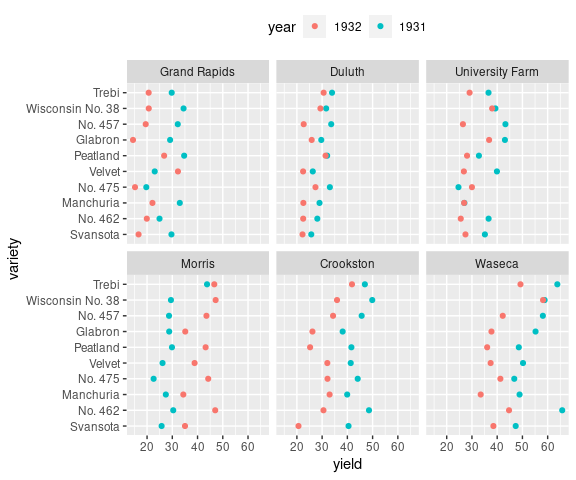
ggplot(barley) +
geom_point(aes(x = yield,
y = variety,
color = year)) +
facet_wrap(~ site) +
theme(legend.position = "top")
This view of the barley data shows lower yields for 1932 than for 1931 for all sites except Morris.
Heat Maps
Heat maps encode a numeric variable as the color of a tile placed at a particular position in a grid.
Heat maps are also called matrix charts or image plots .
Heat maps can be effective in cases where a line plot contains too much over-potting, such as
gma <- filter(gapminder, continent == "Americas")
ggplot(gma) +
geom_line(aes(x = year,
y = lifeExp,
color = country)) +
theme(legend.position = "top",
legend.title = element_blank())
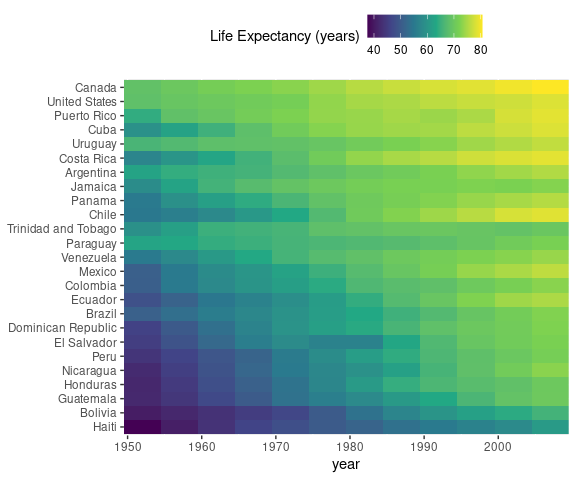
A heat map of these data:
ggplot(gma) +
geom_tile(aes(x = year,
y = reorder(country, lifeExp),
fill = lifeExp)) +
scale_x_continuous(expand = c(0, 0)) +
scale_fill_viridis_c() +
labs(y = NULL,
fill = "Life Expectancy (years)") +
theme(legend.position = "top")
Again it is useful to consider reordering of categories when there is no natural order.
This heat map orders the countries by average life expectancy.
Bubble Charts
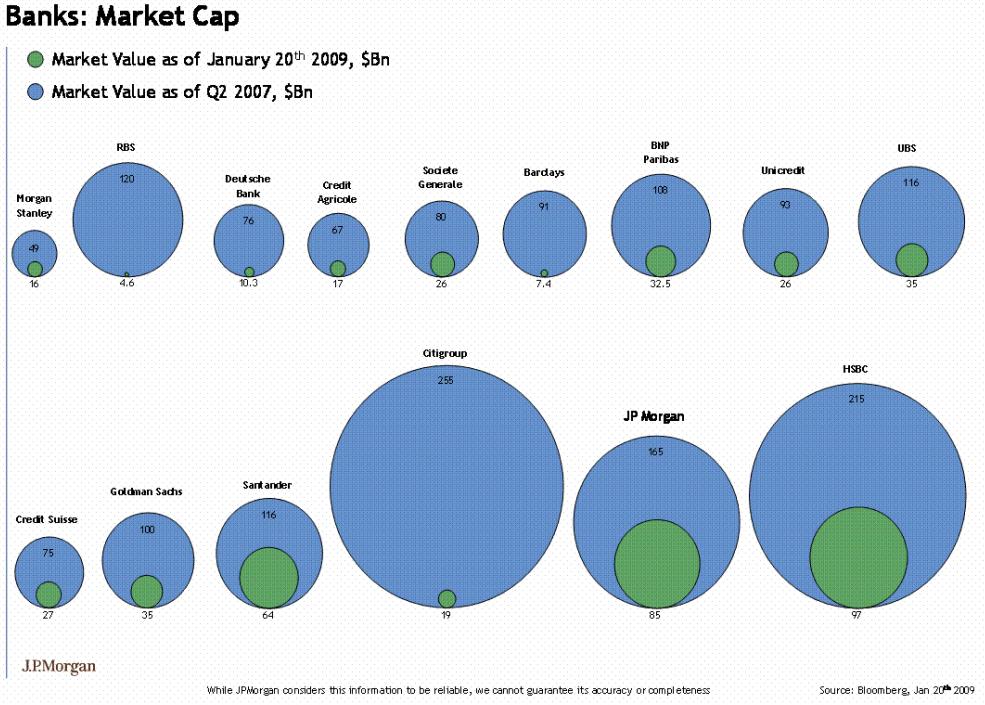
A form of chart often seen in the popular press is the bubble chart .
The bubble chart uses ares of circles to represent magnitudes.
Position in the plane is usually not fully used or not used at all for mapping attributes.
In on-line publications further information on each of the bubbles is often provided through interactions, such as a mouse-over tooltip.
Other charts forms are almost always better for encoding the magnitude information.
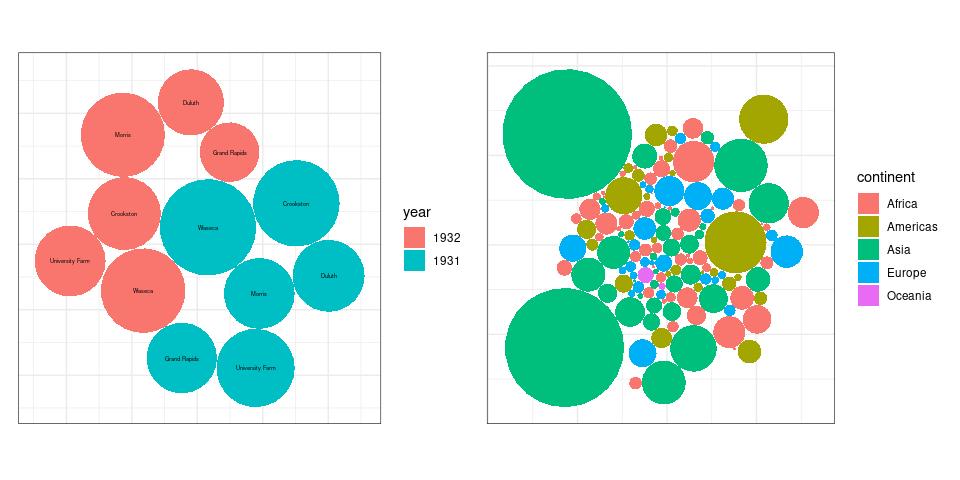
It is also easy to get the encoding wrong (Corrected version ):
ggplot bubble charts for the average yield values from the barley data and for the 2007 population sizes for the gapminder data:
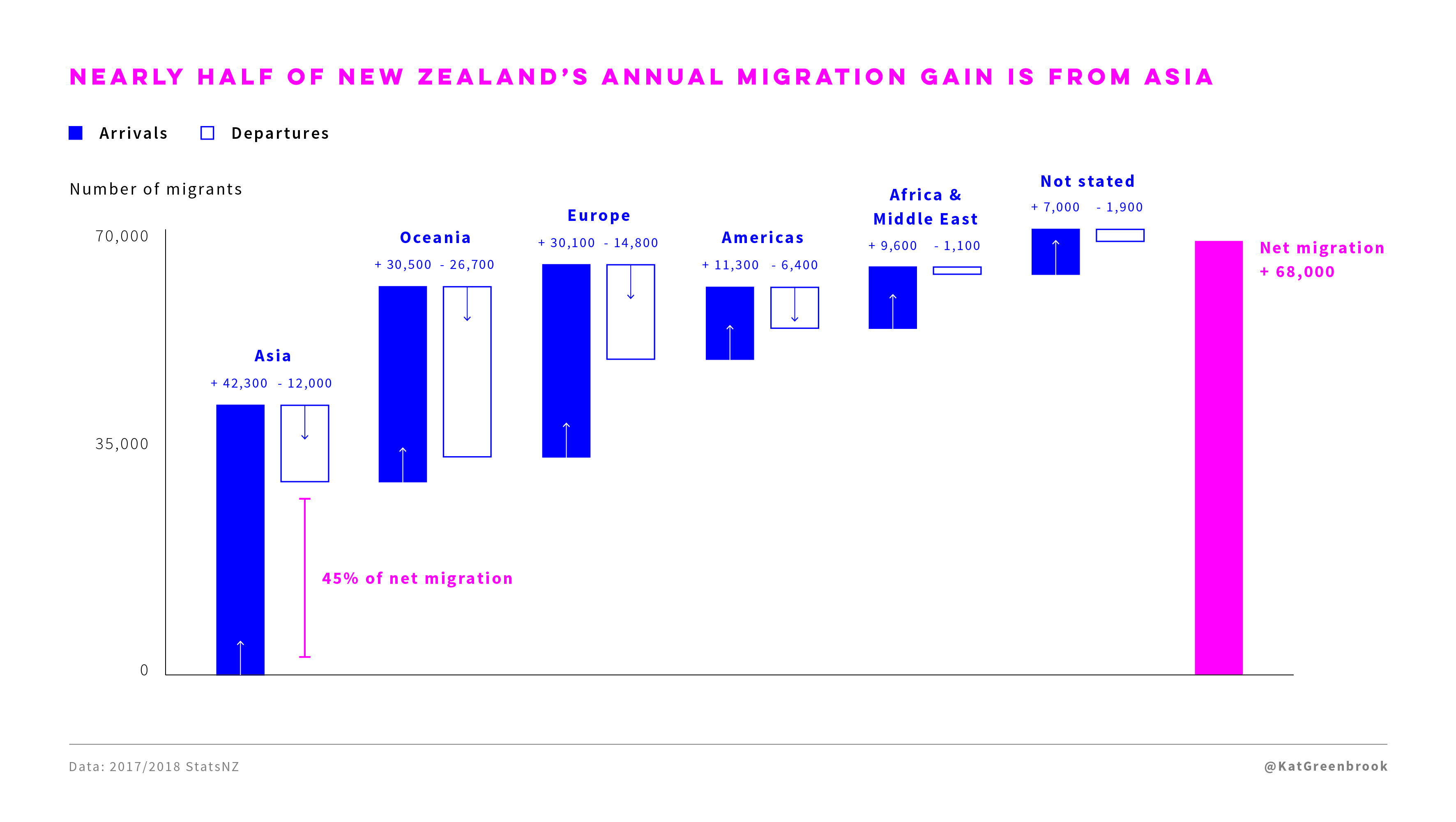
Waterfall Charts
Also called cascade charts .
These usually show the decomposition of a total into positive and negative contributions from various sources.
New Zealand net immigration by region:
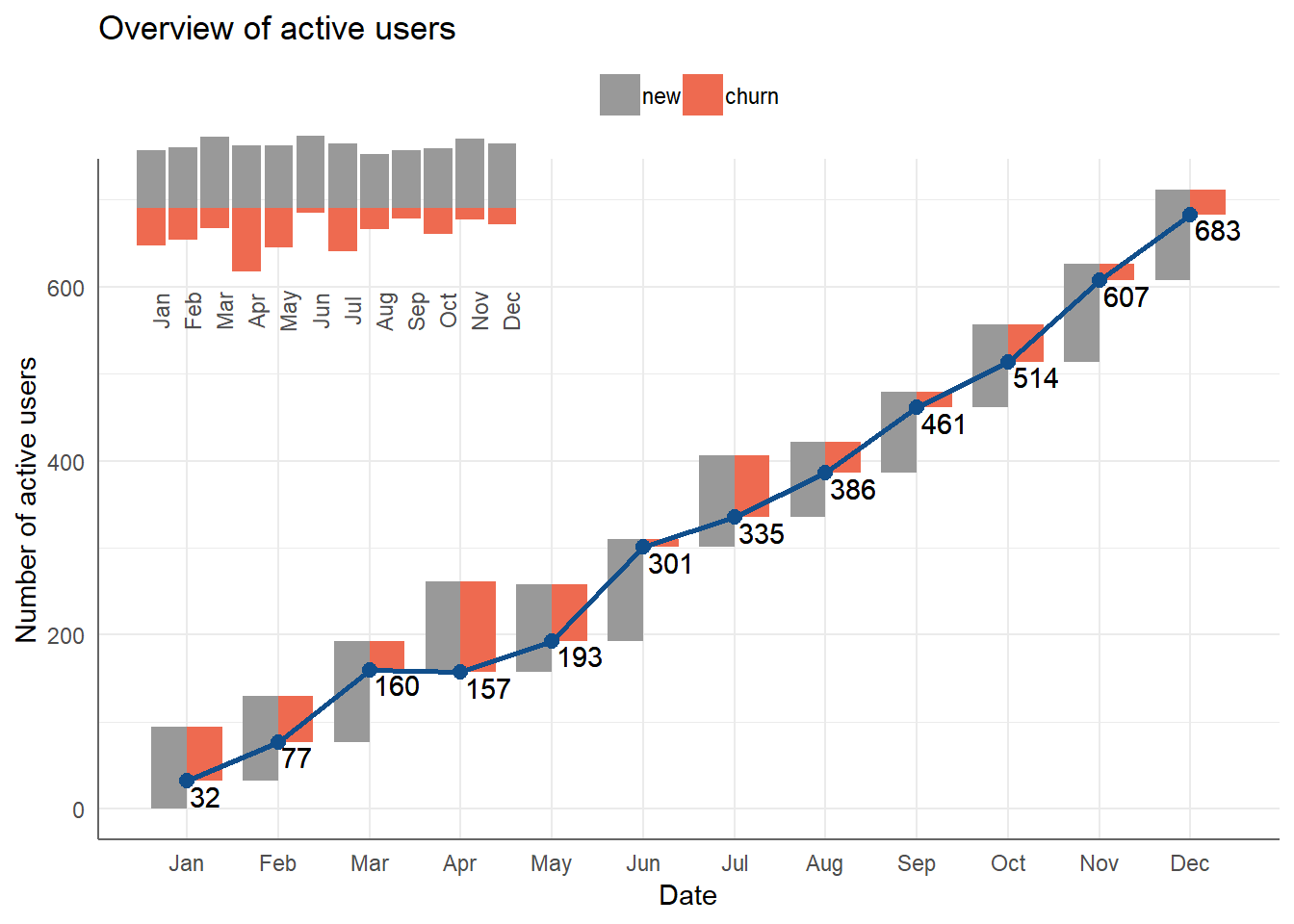
Internet subscribers by month (blog post with ggplot code ).
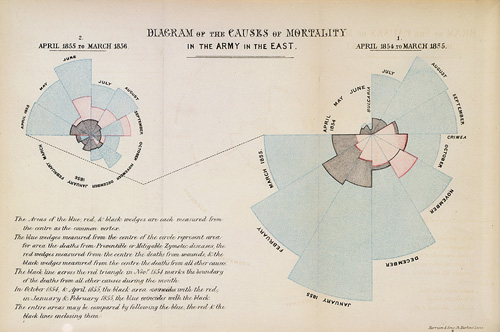
Polar Area Charts
Florence Nightingale’s famous chart showing the effect of the sanitation improvements in March/April 1855:
This chart has been called a polar area diagrams or a Coxcomb Chart .
It can be viewed as
a bar chart with the bars positioned in front of each other,
transformed to polar coordinates,
with magnitude mapped to area (i.e. square root of magnitude mapped to radius).
The data are available in the HistData package as data frame Nightingale.
Some rearrangement of the data is needed to get it into a form amenable for plotting.
library(forcats)
data(Nightingale, package = "HistData")
Night <-
mutate(Nightingale,
Period =
ifelse(Date < as.Date("1855-04-01"),
"Before",
"After"),
Period =
factor(Period, c("Before", "After")),
Month = factor(Month, month.abb)) |>
select(Date, Month, Year, Period,
Disease, Wounds, Other) |>
pivot_longer(5 : 7,
names_to = "Cause",
values_to = "Deaths")
## Rearrange the Month levels to start with April.
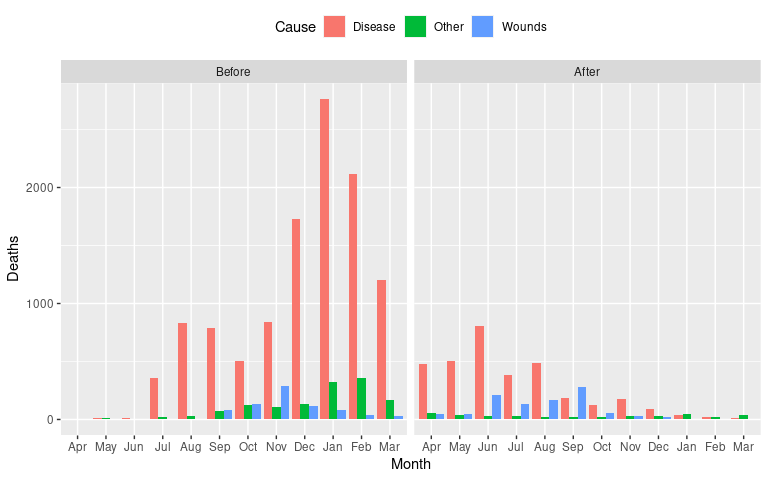
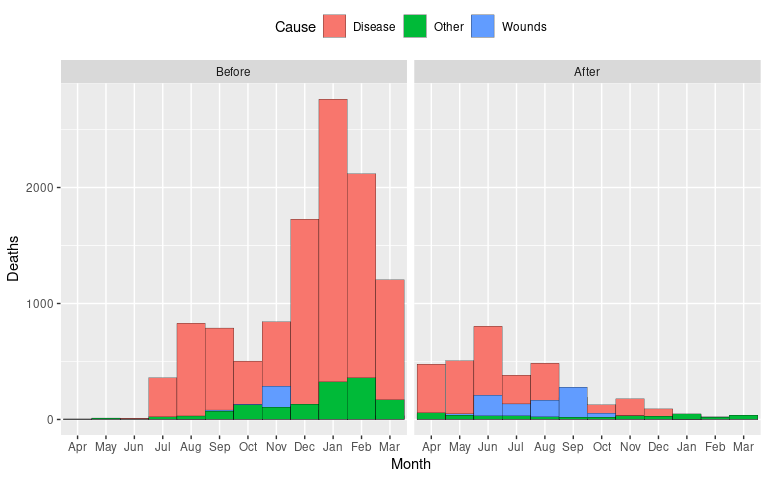
Night3 <- mutate(Night, Month = fct_shift(Month, 3))A standard stacked bar chart of the data:
ggplot(Night3,
aes(x = Month, y = Deaths, fill = Cause)) +
geom_col() +
facet_wrap(~ Period) +
theme(legend.position = "top")
A grouped bar chart of the data:
ggplot(Night3,
aes(x = Month, y = Deaths, fill = Cause)) +
geom_col(position = "dodge") +
facet_wrap(~ Period) +
theme(legend.position = "top")
Using position = "identity" the bars will be placed in front of each other rather than side by side or stacked.
p <- ggplot(Night3,
aes(x = Month, y = Deaths, fill = Cause)) +
geom_col(position = "identity", ## bars in front of each other
width = 1, ## remove space between bars
color = "black", ## bar border color
linewidth = 0.1) + ## bar border thickness
facet_wrap(~ Period) +
theme(legend.position = "top")
p
Problem: Larger bars may be placed in front of smaller ones.
Reordering the Deaths values from largest to smallest ensures that larger bars do not cover smaller ones.
p <- ggplot(arrange(Night3, desc(Deaths)),
aes(x = Month, y = Deaths, fill = Cause)) +
geom_col(position = "identity", ## bars in front of each other
width = 1, ## remove space between bars
color = "black", ## bar border color
linewidth = 0.1) + ## bar border thickness
facet_wrap(~ Period) +
theme(legend.position = "top")
p
Changing to polar coordinates and mapping square roots of Deaths to radius produces the basic polar area chart:
p %+% (arrange(Night3, desc(Deaths)) |>
mutate(Deaths = sqrt(Deaths))) +
coord_polar()
Some adjustments bring the result closer to the original:
p %+%
(arrange(Night, desc(Deaths)) |>
mutate(Month = fct_shift(Month, 6),
Period = factor(Period,
c("After", "Before")),
Deaths = sqrt(Deaths))) +
coord_polar() +
scale_fill_manual(
values = c(Wounds = "pink",
Other = "darkgray",
Disease = "lightblue")) +
theme(axis.title = element_blank(),
axis.text.y = element_blank(),
axis.ticks = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
panel.border = element_blank())
Base and Lattice Graphics
Base graphics provides the dotchart() function for creating dot plots:
with(le_am_2007,
dotchart(sort(lifeExp),
labels = country[order(lifeExp)]))
The lattice package provides dotplot():
library(lattice)
dotplot(reorder(country, lifeExp) ~ lifeExp,
data = le_am_2007)
Most lattice plots support a group argument that is usually mapped to color:
dotplot(reorder(country, lifeExp) ~ lifeExp,
group = year, data = le2, auto.key = TRUE)
Creating a basic bar chart in lattice uses the barchart() function.
## By default lattice creates a bad bar chart with a
## non-zero base line for these data. Fix that by
## specifying xlim = c(0, 85).
barchart(reorder(country, lifeExp) ~ lifeExp,
data = le_am_2007, xlim = c(0, 85))
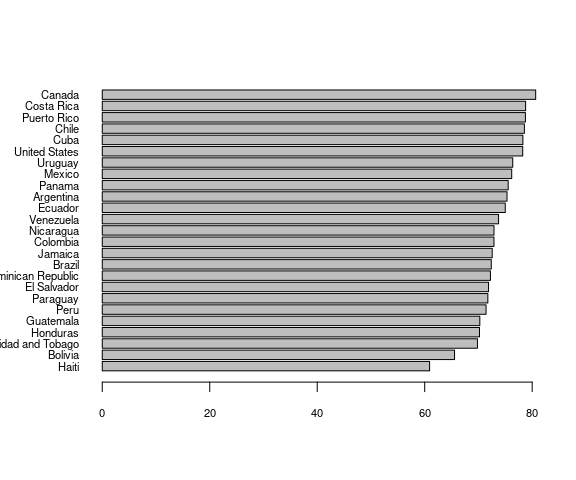
Base graphics also provides a bar chart with the barplot() function.
par(mar = c(5, 5, 4, 2) + 0.1)
with(le_am_2007,
barplot(sort(lifeExp),
horiz = TRUE,
names.arg = country[order(lifeExp)],
las = 1,
cex.names = 0.7,
cex.axis = 0.7))
Interactive Tutorial
An interactive learnravailable .
You can run the tutorial with
STAT4580::runTutorial("amounts")You can install the current version of the STAT4580 package with
remotes::install_gitlab("luke-tierney/STAT4580")You may need to install the remotes package from CRAN first.
Exercises
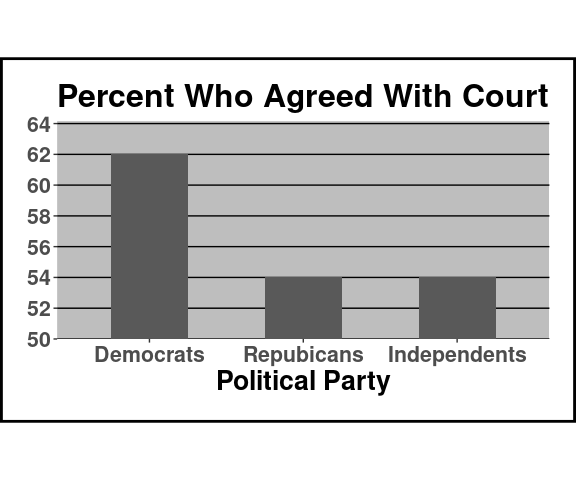
A plot similar to this was featured in a CNN news story several years ago:
Which of the following is approximately correct:
About the same number of democrats as republicans agreed with the court.
About 15% more democrats than republicans agreed with the court.
About tree times as many democrats than republicans agreed with the court.
About two times as many democrats than republicans agreed with the court.
Consider the stacked bar chart produced by the following code:
library(tidyverse)
mpg2 <- mutate(mpg,
class = fct_rev(fct_infreq(class)),
cyl = factor(cyl))
p <- ggplot(mpg2, aes(y = class, fill = cyl)) +
geom_bar()Which of these modifications makes it easiest to compare the count of 4-cylinder models within the different classes?
p %+% mutate(mpg2, cyl = factor(cyl, c(4, 5, 6, 8)))p %+% mutate(mpg2, cyl = factor(cyl, c(8, 6, 5, 4)))p %+% mutate(mpg2, cyl = factor(cyl, c(5, 6, 4, 8)))p %+% mutate(mpg2, cyl = factor(cyl, c(4, 6, 8, 5))) The bar chart produced by the following code has x axis labels that could be improved:
library(gapminder)
library(dplyr)
library(ggplot2)
library(scales)
p <- filter(gapminder, year == 2007) |>
group_by(continent) |>
summarize(avgGdpPercap = mean(gdpPercap)) |>
ggplot(aes(x = avgGdpPercap, y = continent)) +
geom_col() +
labs(x = "Average GDP Per Capita", y = NULL) +
theme_minimal() + theme(text = element_text(size = 16))There are a number of different options. Which of the following does not provide improved x axis labels?
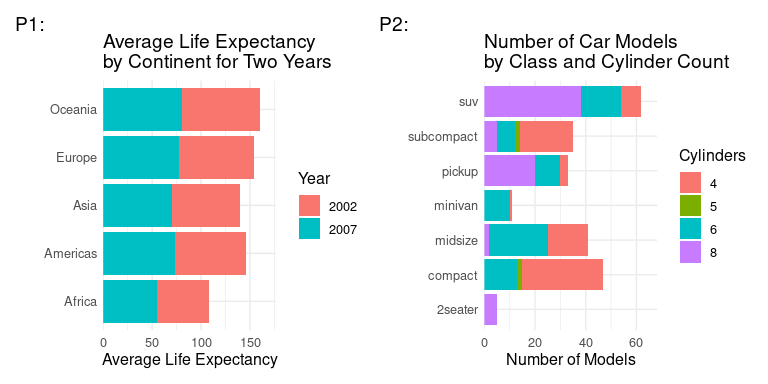
p + scale_x_continuous(labels = label_comma())p + scale_x_continuous(labels = label_dollar())p + scale_x_continuous(labels = unit_format(scale = 1/1000, unit = "K", prefix = "$"))p + scale_x_continuous(labels = c("$10,000", "$20,000", "$30,000")) A stacked bar chart is appropriate if the combined bar heights of the stacked bars have a reasonable interpretation. Consider the following two plots:
library(gapminder)
library(dplyr)
library(ggplot2)
library(patchwork)
p1 <- filter(gapminder, year >= 2000) |>
group_by(continent, year) |>
summarize(avgLifeExp = mean(lifeExp), .groups = "drop") |>
ggplot(aes(x = avgLifeExp, y = continent, fill = factor(year))) +
geom_col() +
theme_minimal() +
theme(text = element_text(size = 12)) +
scale_x_continuous(expand = expansion(mult = c(0, .1))) +
labs(x = "Average Life Expectancy",
y = NULL,
fill = "Year",
title = "Average Life Expectancy\nby Continent for Two Years",
tag = "P1:")
p2 <- count(mpg, class, cyl) |>
ggplot(aes(x = n, y = class, fill = factor(cyl))) +
geom_col() +
theme_minimal() +
theme(text = element_text(size = 12)) +
scale_x_continuous(expand = expansion(mult = c(0, .1))) +
labs(x = "Number of Models",
y = NULL,
fill = "Cylinders",
title = "Number of Car Models\nby Class and Cylinder Count",
tag = "P2:")
p1 + p2
Which of the following statements is true:
P1 is an appropriate use of a stacked bar chart but P2 is not.
P2 is an appropriate use of a stacked bar chart but P1 is not.
Neither P1 nor P2 is an appropriate use of a stacked bar chart.
Both P1 and P2 are appropriate uses of a stacked bar chart.
LS0tCnRpdGxlOiAiVmlzdWFsaXppbmcgQW1vdW50cyIKb3V0cHV0OgogIGh0bWxfZG9jdW1lbnQ6CiAgICB0b2M6IHllcwogICAgY29kZV9mb2xkaW5nOiAiaGlkZSIKICAgIGNvZGVfZG93bmxvYWQ6IHRydWUKLS0tCgo8bGluayByZWw9InN0eWxlc2hlZXQiIGhyZWY9InN0YXQ0NTgwLmNzcyIgdHlwZT0idGV4dC9jc3MiIC8+CjwhLS0gdGl0bGUgYmFzZWQgb24gV2lsa2UncyBjaGFwdGVyIC0tPgoKYGBge3Igc2V0dXAsIGluY2x1ZGUgPSBGQUxTRX0Kc291cmNlKGhlcmU6OmhlcmUoInNldHVwLlIiKSkKa25pdHI6Om9wdHNfY2h1bmskc2V0KGNvbGxhcHNlID0gVFJVRSwgbWVzc2FnZSA9IEZBTFNFLAogICAgICAgICAgICAgICAgICAgICAgZmlnLmhlaWdodCA9IDUsIGZpZy53aWR0aCA9IDYsIGZpZy5hbGlnbiA9ICJjZW50ZXIiKQoKbGlicmFyeShsYXR0aWNlKQpsaWJyYXJ5KHRpZHl2ZXJzZSkKbGlicmFyeShncmlkRXh0cmEpCmxpYnJhcnkoc2NhbGVzKQpzZXQuc2VlZCgxMjM0NSkKYGBgCgpgYGB7ciwgaW5jbHVkZSA9IEZBTFNFfQpzb3VyY2UoaGVyZTo6aGVyZSgiZGF0YXNldHMuUiIpKQpgYGAKCgojIyBWaXN1YWxpemF0aW9uIGFuZCBDb21wYXJpc29uCgpBIHZpc3VhbGl6YXRpb24gb2YgYSBzaW5nbGUgdmFsdWUgd2l0aG91dCBzb21lIGNvbXBhcmF0aXZlIGNvbnRleHQgaXMKcmFyZWx5IHVzZWZ1bAoKYGBge3IsIGVjaG8gPSBGQUxTRX0KbGlicmFyeShnZ3Bsb3QyKQpsaWJyYXJ5KHNjYWxlcykKZ2dwbG90KCkgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IDAsIHkgPSAwKSwKICAgICAgICAgICAgICAgc2hhcGUgPSAyMSwgc2l6ZSA9IDE1MCwgZmlsbCA9IG11dGVkKCJibHVlIikpICsKICAgIGdlb21fdGV4dChhZXMoeCA9IDAsIHkgPSAwLCBsYWJlbCA9IDIwMCksIHNpemUgPSA1MCwgY29sb3IgPSAid2hpdGUiKSArCiAgICB0aGVtZV92b2lkKCkKYGBgCgpVc2VmdWwgdmlzdWFsaXphdGlvbnMgYWxtb3N0IGFsd2F5cyBpbnZvbHZlIGNvbXBhcmlzb25zLgoKKiBwb3NpdGlvbiBvZiBhIHZhbHVlIG9uIGFuIGF4aXMKCiogcmVsYXRpdmUgcG9zaXRpb24gb2YgdHdvIHZhbHVlcwoKKiByZWxhdGl2ZSBtYWduaXR1ZGVzIG9mIHR3byB2YWx1ZXMKCkEgc2ltcGxlIGFuZCBjb21tb24gc2V0dGluZzogVmlzdWFsaXppbmcgYSBtZWFzdXJlbWVudCBvciBzdW1tYXJ5IGZvcgplYWNoIG9mIGEgc2V0IG9mIGNhdGVnb3JpZXMuCgpTb21lIG9mIHRoZSBtb3JlIGNvbW1vbiB2aXN1YWxpemF0aW9uczoKCiogRG90IENoYXJ0cyAoYWxzbyBjYWxsZWQgQ2xldmVsYW5kIERvdCBDaGFydHMpCgoqIEJhciBDaGFydHMKICAqIEdyb3VwZWQgQmFyIENoYXJ0cyAoQ2x1c3RlcmVkIEJhciBDaGFydHMpCiAgKiBTdGFja2VkIEJhciBDaGFydHMKICAqIERpdmVyZ2luZyBCYXIgQ2hhcnRzCgoqIEhlYXQgTWFwcwoKKiBCdWJibGUgQ2hhcnRzCgpTb21lIGxlc3MgZnJlcXVlbnRseSB1c2VkIHZpc3VhbGl6YXRpb25zOgoKKiBXYXRlcmZhbGwgQ2hhcnRzCiogUG9sYXIgQXJlYSBDaGFydHMgKENveGNvbWIgQ2hhcnRzKQoqIER1bWJiZWxsIENoYXJ0cwoKU29tZSBxdWVzdGlvbnMgdG8ga2VlcCBpbiBtaW5kOgoKKiBXaGF0IGNvbXBhcmlzb25zIGFuZCBvdGhlciBhc3Nlc3NtZW50cyBkbyB0aGVzZSB2aXN1YWxpemF0aW9ucyBzdXBwb3J0PwoKKiBIb3cgZG8gdGhlc2UgdmlzdWFsaXphdGlvbnMgc2NhbGUgdG8gbGFyZ2VyIGRhdGEgc2V0cz8KCgojIyBEb3QgUGxvdHMKCgojIyMgQmFzaWNzCgpPbmUgb2YgdGhlIHNpbXBsZXN0IHZpc3VhbGl6YXRpb25zIG9mIGEgc2luZ2xlIG51bWVyaWNhbCB2YXJpYWJsZSB3aXRoCmEgbW9kZXN0IG51bWJlciBvZiBvYnNlcnZhdGlvbnMgYW5kIGxhYmVscyBmb3IgdGhlIG9ic2VydmF0aW9ucyBpcyBhCl9kb3QgcGxvdF8sIG9yIF9DbGV2ZWxhbmQgZG90IHBsb3RfOgoKYGBge3IsIG1lc3NhZ2UgPSBGQUxTRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxpYnJhcnkoZHBseXIpCmxpYnJhcnkoZ2dwbG90MikKbGlicmFyeShnYXBtaW5kZXIpCmxlX2FtXzIwMDcgPC0gZmlsdGVyKGdhcG1pbmRlciwKICAgICAgICAgICAgICAgICAgICAgeWVhciA9PSAyMDA3LAogICAgICAgICAgICAgICAgICAgICBjb250aW5lbnQgPT0gIkFtZXJpY2FzIikKdGhtIDwtIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxNikpCmdncGxvdChsZV9hbV8yMDA3LAogICAgICAgYWVzKHkgPSBjb3VudHJ5LCB4ID0gbGlmZUV4cCkpICsKICAgIGdlb21fcG9pbnQoY29sb3IgPSAiZGVlcHNreWJsdWUzIiwKICAgICAgICAgICAgICAgc2l6ZSA9IDIpICsKICAgIGxhYnMoeCA9ICJMaWZlIEV4cGVjdGFuY3kgKHllYXJzKSIsCiAgICAgICAgIHkgPSBOVUxMKSArCiAgICB0aG0KYGBgCmBgYHtyLCBlY2hvID0gRkFMU0UsIGV2YWwgPSBGQUxTRX0KIyMgdG8gb3JkZXIgYWxwaGFiZXRpY2FsbHkgZnJvbSB0b3AgdG8gYm90dG9tOgpsZV9hbV8yMDA3IDwtIG11dGF0ZShsZV9hbV8yMDA3LAogICAgICAgICAgICAgICAgICAgICBjb3VudHJ5ID0gZmFjdG9yKGNvdW50cnksIHJldihzb3J0KHVuaXF1ZShjb3VudHJ5KSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBkZXNjZW5kaW5nID0gVFJVKSkpKQpgYGAKClRoaXMgdmlzdWFsaXphdGlvbgoKKiBzaG93cyB0aGUgb3ZlcmFsbCBkaXN0cmlidXRpb24gb2YgdGhlIGRhdGEsIGFuZAoKKiBtYWtlcyBpdCBlYXN5IHRvIGxvY2F0ZSB0aGUgbGlmZSBleHBlY3RhbmN5IG9mIGEgcGFydGljdWxhciBjb3VudHJ5LgoKVW5sZXNzIHRoZXJlIGlzIGEgbmF0dXJhbCBvcmRlciB0byB0aGUgY2F0ZWdvcmllcyAoZS5nLiBtb250aHMgb2YgdGhlCnllYXIgb3IgZGF5cyBvZiB0aGUgd2VlaykgaXQgaXMgdXN1YWxseSBiZXR0ZXIgdG8gcmVvcmRlciB0byBtYWtlIHRoZQpwbG90IGluY3JlYXNpbmcgb3IgZGVjcmVhc2luZzoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGxlX2FtXzIwMDcsCiAgICAgICBhZXMoeSA9IHJlb3JkZXIoY291bnRyeSwgbGlmZUV4cCksCiAgICAgICAgICAgeCA9IGxpZmVFeHApKSArCiAgICBnZW9tX3BvaW50KGNvbG9yID0gImRlZXBza3libHVlMyIsCiAgICAgICAgICAgICAgIHNpemUgPSAyKSArCiAgICBsYWJzKHggPSAiTGlmZSBFeHBlY3RhbmN5ICh5ZWFycykiLAogICAgICAgICB5ID0gTlVMTCkgKwogICAgdGhtCmBgYAoKKiBMb2NhdGluZyBhIHBhcnRpY3VsYXIgY291bnRyeSBpcyBhIGxpdHRsZSBtb3JlIGRpZmZpY3VsdC4KCiogQnV0IHRoZSBzaGFwZSBvZiB0aGUgZGlzdHJpYnV0aW9uIGlzIG1vcmUgYXBwYXJlbnQuCgoqIEFwcHJveGltYXRlIG1lZGlhbiBhbmQgcXVhcnRpbGVzIGNhbiBiZSByZWFkIG9mZiBlYXNpbHkuCgpEb3QgcGxvdHMgYXJlIHBhcnRpY3VsYXJseSBhcHByb3ByaWF0ZSBmb3IgaW50ZXJ2YWwgZGF0YS4KCiogdGhleSBvZnRlbiBkbyBub3Qgc2hvdyB0aGUgb3JpZ2luOwoKKiB0aGV5IGZvY3VzIHRoZSB2aWV3ZXIncyBhdHRlbnRpb24gb24gZGlmZmVyZW5jZXMuCgpEb3QgcGxvdHMgYXJlIG9mdGVuIHZlcnkgdXNlZnVsIGZvciBncm91cCBzdW1tYXJpZXMgbGlrZSB0b3RhbHMgb3IKYXZlcmFnZXMuCgpGb3IgdGhlIGBiYXJsZXlgIGRhdGEsIHRvdGFsIHlpZWxkIHdpdGhpbiBlYWNoIHNpdGUsIGFkZGluZyB1cAphY3Jvc3MgYWxsIHZhcmlldGllcyBhbmQgYm90aCB5ZWFycywgY2FuIGJlIGNvbXB1dGVkIGFzCgpgYGB7cn0KYl90b3Rfc2l0ZSA8LQogICAgZ3JvdXBfYnkoYmFybGV5LCBzaXRlKSB8PgogICAgc3VtbWFyaXplKHlpZWxkID0gc3VtKHlpZWxkKSkKYGBgCgpUaGUgdG90YWxzIGNhbiB0aGVuIGJlIHZpc3VhbGl6ZWQgaW4gYSBkb3QgcGxvdDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGJfdG90X3NpdGUsIGFlcyh4ID0geWllbGQsIHkgPSBzaXRlKSkgKwogICAgZ2VvbV9wb2ludChjb2xvciA9ICJkZWVwc2t5Ymx1ZTMiLCBzaXplID0gMi41KSArCiAgICBsYWJzKHggPSAiVG90YWwgWWllbGQgKGJ1c2hlbHMvYWNyZSkiLCB5ID0gTlVMTCkgKwogICAgdGhtCmBgYAoKCiMjIyBMYXJnZXIgRGF0YSBTZXRzCgpGb3IgbGFyZ2VyIGRhdGEgc2V0cywgbGlrZSB0aGUgYGNpdHl0ZW1wc2AgZGF0YSB3aXRoIGByIG5yb3coY2l0eXRlbXBzKWAKb2JzZXJ2YXRpb25zLCBvdmVyLXBsb3R0aW5nIG9mIGxhYmVscyBiZWNvbWVzIGEgcHJvYmxlbToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGNpdHl0ZW1wcywKICAgICAgIGFlcyh4ID0gdGVtcCwgeSA9IHJlb3JkZXIoY2l0eSwgdGVtcCkpKSArCiAgICBnZW9tX3BvaW50KGNvbG9yID0gImRlZXBza3libHVlMyIsIHNpemUgPSAwLjUpICsKICAgIGxhYnMoeCA9ICJUZW1wZXJhdHVyZSAoZGVncmVlcyBGKSIsIHkgPSBOVUxMKSArCiAgICB0aG0KYGBgCgpSZWR1Y2luZyB0byAzMCBvciA0MCwgZS5nLiBieSB0YWtpbmcgYSBzYW1wbGUgb3IgYSBtZWFuaW5nZnVsIHN1YnNldCwKY2FuIGhlbHA6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmN0MSA8LSBmaWx0ZXIoY2l0eXRlbXBzLCB0ZW1wIDwgMzIpIHw+IHNhbXBsZV9uKDEwKQpjdDIgPC0gZmlsdGVyKGNpdHl0ZW1wcywgdGVtcCA+PSAzMikgfD4gc2FtcGxlX24oMjApCmN0c2FtcCA8LSBiaW5kX3Jvd3MoY3QxLCBjdDIpCmdncGxvdChjdHNhbXAsCiAgICAgICBhZXMoeCA9IHRlbXAsIHkgPSByZW9yZGVyKGNpdHksIHRlbXApKSkgKwogICAgZ2VvbV9wb2ludChjb2xvciA9ICJkZWVwc2t5Ymx1ZTMiLCBzaXplID0gMikgKwogICAgbGFicyh4ID0gIlRlbXBlcmF0dXJlIChkZWdyZWVzIEYpIiwgeSA9IE5VTEwpICsKICAgIHRobQpgYGAKCgojIyMgU29tZSBWYXJpYXRpb25zCgpUaGUgc2l6ZSBvZiB0aGUgZG90cyBjYW4gYmUgdXNlZCB0byBlbmNvZGUgYW4gYWRkaXRpb25hbCBudW1lcmljCnZhcmlhYmxlLgoKVGhpcyB2aWV3IHVzZXMgYXJlYSB0byBlbmNvZGUgcG9wdWxhdGlvbiBzaXplOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QobGVfYW1fMjAwNywgYWVzKHkgPSByZW9yZGVyKGNvdW50cnksIGxpZmVFeHApLAogICAgICAgICAgICAgICAgICAgICAgIHggPSBsaWZlRXhwLAogICAgICAgICAgICAgICAgICAgICAgIHNpemUgPSBwb3AgLyAxMDAwMDAwKSkgKwogICAgZ2VvbV9wb2ludChjb2wgPSAiZGVlcHNreWJsdWUzIikgKwogICAgbGFicyh4ID0gIkxpZmUgRXhwZWN0YW5jeSAoeWVhcnMpIiwgeSA9IE5VTEwpICsKICAgIHNjYWxlX3NpemVfYXJlYSgiUG9wdWxhdGlvblxuKE1pbGxpb25zKSIsCiAgICAgICAgICAgICAgICAgICAgbWF4X3NpemUgPSA4KSArCiAgICB0aG0gKyB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKYGBgCgpUaGlzIGlzIHNvbWV0aW1lcyBjYWxsZWQgYSBfYnViYmxlIGNoYXJ0Xy4KClJlcGVhdGVkIG1lYXN1cmVzLCBzdWNoIGFzIHZhbHVlcyBmb3IgMjAwMiBhbmQgMjAwNywgY2FuIGJlIHNob3duIGFuZApkaXN0aW5ndWlzaGVkIGJ5IGNvbG9yLCBzaGFwZSwgb3IgYm90aC4KClVzaW5nIGNvbG9yOgoKYGBge3IgZ2FwbWluZGVyLWRvdHBsb3QtdHdvLXllYXIsIGVjaG8gPSBGQUxTRX0KYGBgCgpgYGB7ciBnYXBtaW5kZXItZG90cGxvdC10d28teWVhciwgZXZhbCA9IEZBTFNFLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KIyMgZmlsdGVyIGRvd24gdG8gZGF0YSBmb3IgMjAwMiBhbmQgMjAwNwojIyBmb3IgdGhlIEFtZXJpY2FzCmxlMiA8LSBmaWx0ZXIoZ2FwbWluZGVyLAogICAgICAgICAgICAgIHllYXIgPj0gMjAwMiwKICAgICAgICAgICAgICBjb250aW5lbnQgPT0gIkFtZXJpY2FzIikKCiMjIG1ha2UgYSBmYWN0b3IgWWVhciB0byBnZXQgYSBkaXNjcmV0ZSBjb2xvcgojIyBwYWxldHRlLCBub3QgYSBjb250aW51b3VzIG9uZQpsZTIgPC0gbXV0YXRlKGxlMiwgWWVhciA9IGZhY3Rvcih5ZWFyKSkKCmdncGxvdChsZTIsIGFlcyh5ID0gcmVvcmRlcihjb3VudHJ5LCBsaWZlRXhwKSwKICAgICAgICAgICAgICAgIHggPSBsaWZlRXhwLAogICAgICAgICAgICAgICAgY29sb3IgPSBZZWFyKSkgKwogICAgZ2VvbV9wb2ludCgpICsKICAgIGxhYnMoeCA9ICJMaWZlIEV4cGVjdGFuY3kgKHllYXJzKSIsIHkgPSBOVUxMKSArCiAgICB0aG0gKyB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKYGBgCgoqIEFsbCBjb3VudHJpZXMgc2hvdyBzb21lIGltcHJvdmVtZW50IGluIGxpZmUgZXhwZWN0YW5jeS4KCiogVGhlIHNtYWxsIGltcHJvdmVtZW50IGZvciBKYW1haWNhIF9wb3BzIG91dF8gYSBiaXQuCgpVc2luZyBzaGFwZSBmb3IgdGhlIGBiYXJsZXlgIGRhdGE6CgpgYGB7cn0KYl90b3QgPC0KICAgIGdyb3VwX2J5KGJhcmxleSwgc2l0ZSwgeWVhcikgfD4KICAgIHN1bW1hcml6ZSh5aWVsZCA9IHN1bSh5aWVsZCksIC5ncm91cHMgPSAiZHJvcCIpCmdncGxvdChiX3RvdCwgYWVzKHggPSB5aWVsZCwgeSA9IHNpdGUsIHNoYXBlID0geWVhcikpICsKICAgIGdlb21fcG9pbnQoY29sb3IgPSAiZGVlcHNreWJsdWUzIiwgc2l6ZSA9IDMpICsKICAgIGxhYnMoeCA9ICJUb3RhbCBZaWVsZCAoYnVzaGVscy9hY3JlKSIsIHkgPSBOVUxMKSArCiAgICB0aG0gKyB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKYGBgCgpGb3IgcmVwZWF0ZWQgdHdvIHZhbHVlcyBwZXIgY2xhc3MgaXQgY2FuIGhlbHAgdG8gY29ubmVjdCB0aGUgdHdvIGRvdHMuCgpUaGlzIHZpc3VhbGx5IGVtcGhhc2l6ZXMgdGhlIHJlbGF0aXZlIHNpemVzIG9mIGRpZmZlcmVuY2VzLgoKVGhlIHJlc3VsdCBpcyBzb21ldGltZXMgY2FsbGVkIGEgX2R1bWJiZWxsIGNoYXJ0Xy4KCkZvciB0aGUgYmFybGV5IHlpZWxkcyBkYXRhOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoYl90b3QsIGFlcyh4ID0geWllbGQsIHkgPSBzaXRlKSkgKwogICAgZ2VvbV9saW5lKGFlcyhncm91cCA9IHNpdGUpLAogICAgICAgICAgICAgIGxpbmV3aWR0aCA9IDIsCiAgICAgICAgICAgICAgY29sb3IgPSAiZ3JleSIpICsKICAgIGdlb21fcG9pbnQoYWVzKGNvbG9yID0geWVhciksIHNpemUgPSA0KSArCiAgICBsYWJzKHggPSAiVG90YWwgWWllbGQgKGJ1c2hlbHMvYWNyZSkiLCB5ID0gTlVMTCkgKwogICAgdGhtICsgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpCmBgYAoKRm9yIHRoZSBHYXBtaW5kZXIgbGlmZSBleHBlY3RhbmN5IGRhdGE6CgpgYGB7ciwgZWNobyA9IEZBTFNFLCBldmFsID0gRkFMU0V9CmxpYnJhcnkoZ2dhbHQpCmxpYnJhcnkoc2NhbGVzKQpwaXZvdF93aWRlcihiX3RvdCwKICAgICAgICAgICAgbmFtZXNfZnJvbSA9ICJ5ZWFyIiwKICAgICAgICAgICAgdmFsdWVzX2Zyb20gPSAieWllbGQiLAogICAgICAgICAgICBuYW1lc19wcmVmaXggPSAiWCIpIHw+CiAgICBnZ3Bsb3QoYWVzKHggPSBYMTkzMSwgeSA9IHNpdGUsIHhlbmQgPSBYMTkzMikpICsKICAgIGdlb21fZHVtYmJlbGwoc2l6ZSA9IDMsIGNvbG9yID0gImdyZXkiLAogICAgICAgICAgICAgICAgICBjb2xvcl94ID0gbXV0ZWQoInJlZCIpLCBjb2xvcl94ZW5kID0gbXV0ZWQoImJsdWUiKSwKICAgICAgICAgICAgICAgICAgZG90X2d1aWRlID0gVFJVRSkKYGBgCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChsZTIsIGFlcyh5ID0gcmVvcmRlcihjb3VudHJ5LCBsaWZlRXhwKSwKICAgICAgICAgICAgICAgIHggPSBsaWZlRXhwLAogICAgICAgICAgICAgICAgY29sb3IgPSBZZWFyKSkgKwogICAgZ2VvbV9saW5lKGFlcyhncm91cCA9IGNvdW50cnkpLAogICAgICAgICAgICAgIGxpbmV3aWR0aCA9IDEuNSwKICAgICAgICAgICAgICBjb2xvciA9ICJncmV5IikgKwogICAgZ2VvbV9wb2ludChzaXplID0gMi41KSArCiAgICBsYWJzKHggPSAiTGlmZSBFeHBlY3RhbmN5ICh5ZWFycykiLCB5ID0gTlVMTCkgKwogICAgdGhtICsgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpCmBgYAoKCiMjIyBWYXJpYXRpb25zIGluIEFwcGVhcmFuY2UKClRoZSBkb3QgcGxvdHMgaW50cm9kdWNlZCBieSBXLiBTLiBDbGV2ZWxhbmQgaW4gaGlzIDE5OTMgYm9vawpfVmlzdWFsaXppbmcgRGF0YV8gdXNlIG9ubHkgaG9yaXpvbnRhbCBncmlkIGxpbmVzLgoKVGhpcyBhbHNvIGNvcnJlc3BvbmRzIHRvIHRoZSBkb3QgcGxvdHMgcHJvdmlkZWQgYnkgYmFzZSBhbmQgbGF0dGljZQpncmFwaGljcyBhbmQgdG8gdGhlIGRvdCBwbG90IG9idGFpbmVkIHVzaW5nIHRoZSBXYWxsIFN0cmVldCBKb3VybmFsCnRoZW1lIGZyb20gdGhlIGBnZ3RoZW1lc2BwYWNrYWdlOgoKYGBge3IsIGZpZy5oZWlnaHQgPSA1LjUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoYl90b3Rfc2l0ZSwgYWVzKHggPSB5aWVsZCwgeSA9IHNpdGUpKSArCiAgICBnZW9tX3BvaW50KHNpemUgPSAyKSArCiAgICBsYWJzKHggPSAiVG90YWwgWWllbGQgKGJ1c2hlbHMvYWNyZSkiLCB5ID0gTlVMTCkgKwogICAgZ2d0aGVtZXM6OnRoZW1lX3dzaigpCmBgYAoKQSB0aGVtZSB0byBjbG9zZWx5IG1hdGNoIHRoZSBzdHlsZSB1c2VkIGJ5IENsZXZlbGFuZCBjYW4gYmUgZGVmaW5lZCBhcwoKPCEtLQoKIyBodHRwOi8vd3d3Lndpbi12ZWN0b3IuY29tL2Jsb2cvMjAxMy8wMi9yZXZpc2l0aW5nLWNsZXZlbGFuZHMtdGhlLWVsZW1lbnRzLW9mLWdyYXBoaW5nLWRhdGEtaW4tZ2dwbG90Mi8KLS0+CgpgYGB7cn0KdGhlbWVfZG90cGxvdHggPC0gZnVuY3Rpb24oKSB7CiAgICB0aGVtZSgKICAgICAgICAjIyByZW1vdmUgdGhlIHZlcnRpY2FsIGdyaWQgbGluZXMKICAgICAgICBwYW5lbC5ncmlkLm1ham9yLnggPSBlbGVtZW50X2JsYW5rKCksCiAgICAgICAgcGFuZWwuZ3JpZC5taW5vci54ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICMjIGV4cGxpY2l0bHkgc2V0IHRoZSBob3Jpem9udGFsIGxpbmVzCiAgICAgICAgIyMgKG9yIHRoZXkgd2lsbCBkaXNhcHBlYXIgdG9vKQogICAgICAgIHBhbmVsLmdyaWQubWFqb3IueSA9CiAgICAgICAgICAgIGVsZW1lbnRfbGluZShjb2xvciA9ICJibGFjayIsCiAgICAgICAgICAgICAgICAgICAgICAgICBsaW5ldHlwZSA9IDMpLAogICAgICAgIGF4aXMudGV4dC55ID0gZWxlbWVudF90ZXh0KHNpemUgPSByZWwoMS4yKSksCiAgICAgICAgIyMgdXNlIGEgd2hpdGUgYmFja2dyb3Vuc2QKICAgICAgICBwYW5lbC5iYWNrZ3JvdW5kID0KICAgICAgICAgICAgZWxlbWVudF9yZWN0KGZpbGwgPSAid2hpdGUiLAogICAgICAgICAgICAgICAgICAgICAgICAgY29sb3IgPSBOQSksCiAgICAgICAgcGFuZWwuYm9yZGVyID0KICAgICAgICAgICAgZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwKICAgICAgICAgICAgICAgICAgICAgICAgIGNvbG9yID0gImdyZXkyMCIpLAogICAgICAgICMjIGluY3JlYXNlIHRleHQgc2l6ZQogICAgICAgIHRleHQgPSBlbGVtZW50X3RleHQoc2l6ZSA9IDE2KSkKfQpgYGAKClRoaXMgcHJvZHVjZXMKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGJfdG90X3NpdGUsIGFlcyh4ID0geWllbGQsIHkgPSBzaXRlKSkgKwogICAgZ2VvbV9wb2ludChzaXplID0gMikgKwogICAgbGFicyh4ID0gIlRvdGFsIFlpZWxkIChidXNoZWxzL2FjcmUpIiwKICAgICAgICAgeSA9IE5VTEwpICsKICAgIHRoZW1lX2RvdHBsb3R4KCkKYGBgCgoKIyMgQmFyIENoYXJ0cwoKCiMjIyBCYXNpY3MKCkEgYmFzaWMgYmFyIGNoYXJ0OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwIDwtIGdncGxvdChsZV9hbV8yMDA3KSArCiAgICBnZW9tX2NvbChhZXMoeSA9IGxpZmVFeHAsCiAgICAgICAgICAgICAgICAgeCA9IHJlb3JkZXIoY291bnRyeSwgbGlmZUV4cCkpLAogICAgICAgICAgICAgZmlsbCA9ICJkZWVwc2t5Ymx1ZTMiKSArCiAgICBsYWJzKHkgPSAiTGlmZSBFeHBlY3RhbmN5ICh5ZWFycykiLAogICAgICAgICB4ID0gTlVMTCkgKwogICAgc2NhbGVfeV9jb250aW51b3VzKAogICAgICAgIGV4cGFuZCA9IGV4cGFuc2lvbihtdWx0ID0gYygwLCAuMSkpKSArCiAgICB0aG0KcApgYGAKClRoZSBsYWJlbHMgYXJlIGEgbWVzcy4KCiogT25lIG9wdGlvbiBpcyB0byB3cml0ZSBsYWJlbHMgYXQgYW4gYW5nbGUsIGJ1dCB0aGlzIG1ha2VzIHRoZW0gaGFyZCB0byByZWFkLgoKKiBGbGlwcGluZyB0aGUgcGxvdCBpcyB1c3VhbGx5IGEgYmV0dGVyIG9wdGlvbi4KClRvIG1ha2UgbGFiZWxzIHJlYWRhYmxlIHdlIGNhbiBmbGlwIHRoZSBwbG90OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQojIyBSZWRvaW5nIHRoZSBwbG90IHBsb3Qgd2l0aCBgeGAgYW5kIGB5YCBhZXN0aGV0aWNzCiMjIHJldmVyc2VkIGRpZCBub3Qgd29yayBpbiB0aGUgcGFzdCBidXQgZG9lcyB3b3JrIGluCiMjIGN1cnJlbnQgZ2dwbG90MiB2ZXJzaW9ucy4KIyMgQnV0IGNvb3JkX2ZsaXAoKSBpcyBzdGlsbCBzb21ldGltZXMgbmVjZXNzYXJ5LgpwICsgY29vcmRfZmxpcCgpCmBgYAoKCiMjIyBTb21lIE5vdGVzCgpCYXIgY2hhcnRzIHNlZW0gdG8gYmUgdXNlZCBtdWNoIG1vcmUgdGhhbiBkb3QgcGxvdHMgaW4gdGhlIHBvcHVsYXIKbWVkaWEsIGJ1dCB0aGV5IGFyZSBsZXNzIHdpZGVseSBhcHBsaWNhYmxlLgoKUmVzZWFyY2ggb24gdmlzdWFsIHBlcmNlcHRpb24gaGFzIHNob3duIHRoYXQgdmlld2VycyBvZiBiYXIgY2hhcnRzCnN1YmNvbnNjaW91c2x5LCBvciBfcHJlLWF0dGVudGl2ZWx5XywgZm9jdXMgb24gcmVsYXRpdmUgbGVuZ3RocyBvZiBiYXJzLgoKVGhpcyBtZWFucyB0aGF0IGZvciBhIGJhciBjaGFydCB0byBiZSBhcHByb3ByaWF0ZSBhbmQgd29yayB3ZWxsOgoKKiBSYXRpbyBjb21wYXJpc29ucyBoYXZlIHRvIG1ha2Ugc2Vuc2UgZm9yIHlvdSBkYXRhLgoKKiBUaGUgcmVsYXRpdmUgYmFyIGxlbmd0aHMgaGF2ZSB0byBhY2N1cmF0ZWx5IHJlZmxlY3QgdGhhdCBkYXRhIHJhdGlvLgoKVGhpcyBpbiB0dXJuIGltcGxpZXMgdGhhdCBiYXIgY2hhcnRzIHNob3VsZCBfYWx3YXlzXyBoYXZlIGEgemVybyBiYXNlIGxpbmUuCgpZb3UgbWF5IG5lZWQgdG8gaW50ZXJ2ZW5lIHdpdGggeW91ciBzb2Z0d2FyZSdzIGRlZmF1bHRzIHRvIG1ha2UgdGhpcwpoYXBwZW4uCgpDcmVhdGluZyBhIGJhciBjaGFydCB3aXRoIGEgbm9uLXplcm8gYmFzZSBsaW5lIGlzIHBvc3NpYmxlIGluIGBnZ3Bsb3RgCmJ1dCBub3QgZWFzeToKCmBgYHtyLCBtZXNzYWdlID0gRkFMU0UsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpiYXNlbGluZSA8LSA2MAp0aWNrcyA8LSBjKDAsIDEwLCAyMCwgMzApCmdncGxvdChsZV9hbV8yMDA3LAogICAgICAgYWVzKHggPSBsaWZlRXhwIC0gYmFzZWxpbmUsCiAgICAgICAgICAgeSA9IHJlb3JkZXIoY291bnRyeSwgbGlmZUV4cCkpKSArCiAgICBnZW9tX2NvbChmaWxsID0gImRlZXBza3libHVlMyIpICsKICAgIGxhYnMoeCA9ICJMaWZlIEV4cGVjdGFuY3kgKHllYXJzKSIsCiAgICAgICAgIHkgPSBOVUxMKSArCiAgICBzY2FsZV94X2NvbnRpbnVvdXMoCiAgICAgICAgYnJlYWtzID0gdGlja3MsCiAgICAgICAgbGFiZWxzID0gdGlja3MgKyBiYXNlbGluZSwKICAgICAgICBleHBhbmQgPSBleHBhbnNpb24obXVsdCA9IGMoMCwgLjEpKSkgKwogICAgdGhtICsgbGFicyh0aXRsZSA9ICJBIEJhZCBCYXIgQ2hhcnQiKQpgYGAKCiogVGhlIHZpc3VhbCBpbXByZXNzaW9uIGlzIHRoYXQgdGhlIHZhbHVlIGZvciBCb2xpdmlhIGlzIGZpdmUgdGltZXMKICBoaWdoZXIgdGhhbiB0aGUgdmFsdWUgZm9yIEhhaXRpLgoKKiBUaGlzIGlzIF9ub3RfIGFuIGFjY3VyYXRlIHJlcHJlc2VudGF0aW9uIG9mIHRoZSBkYXRhLgoKQmFyIGNoYXJ0cyBhbHdheXMgcHVzaCB0aGUgdmlld2VyIHRvIHJhdGlvIGNvbXBhcmlzb25zLCB3aGV0aGVyCnRoZXkgYXJlIG1lYW5pbmdmdWwgb3Igbm90LgoKVXNpbmcgYSBub24temVybyBiYXNlbGluZSBjYW4gdGhlcmVmb3JlClttaXNsZWFkIHRoZSB2aWV3ZXJdKGh0dHBzOi8vd3d3LnN0b3J5dGVsbGluZ3dpdGhkYXRhLmNvbS9ibG9nLzIwMTIvMDkvYmFyLWNoYXJ0cy1tdXN0LWhhdmUtemVyby1iYXNlbGluZSkuCgpTb21lIG5ld3Mgb3JnYW5pemF0aW9ucyBzZWVtIHBhcnRpY3VsYXJseSBwcm9uZSB0byB0YWtpbmcgYWR2YW50YWdlCm9mL2ZhbGxpbmcgcHJleSB0byB0aGlzIGlzc3VlLgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjcwJSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiYnVzaHRheGJhci5qcGVnIikpCmBgYApgYGB7ciwgZWNobyA9IEZBTFNFLCBvdXQud2lkdGggPSAiNzAlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJvYmFtYWJhci5qcGVnIikpCmBgYAoKQSBbYmxvZwpwb3N0XShodHRwczovL3d3dy5zdGF0c2NoYXQub3JnLm56LzIwMjAvMDIvMDIvZ3JhcGhzLWRvbnQtbWF0dGVyLykKZGlzY3Vzc2VzIGEgY291cnQgY2FzZSBpbiBOZXcgWmVhbGFuZCBhYm91dCBhIG1pc2xlYWRpbmcgYmFyIGNoYXJ0CndpdGggYSBub24temVybyBiYXNlbGluZS4KCkFub3RoZXIgW2Jsb2cKcG9zdF0oaHR0cHM6Ly93d3cuc3Rvcnl0ZWxsaW5nd2l0aGRhdGEuY29tL2Jsb2cvMjAyMC8yLzE5L3doYXQtaXMtYS1iYXItY2hhcnQpCm1heSBhbHNvIGJlIGhlbHBmdWwuCgpbVGhlIGFydCBvZiBtYWtpbmcgc2ltcGxlIHRoaW5ncwpoYXJkZXJdKGh0dHBzOi8vanVua2NoYXJ0cy50eXBlcGFkLmNvbS9qdW5rX2NoYXJ0cy8yMDI0LzAyL3RoZS1hcnQtb2YtbWFraW5nLXNpbXBsZS10aGluZ3MtaGFyZGVyLmh0bWwpIChGZWJydWFyeSAyLCAyMDI0KToKCmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI1MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoIm1zbmJjLWJhZC1iYXItMjAyNC5qcGciKSkKYGBgCgpbRGVmZW5zZSBhZ2FpbnN0IGRpc2hvbmVzdApjaGFydHNdKGh0dHBzOi8vZmxvd2luZ2RhdGEuY29tL3Byb2plY3RzL2Rpc2hvbmVzdC1jaGFydHMvKSAoRmVicnVhcnkKMTMsIDIwMjUpLgoKCiMjIyBEYXRhIFdpdGggQm90aCBQb3NpdGl2ZSBhbmQgTmVnYXRpdmUgVmFsdWVzIAoKQmFyIGNoYXJ0cyBjYW4gYmUgdXNlZCBmb3IgZGF0YSBjb250YWluaW5nIGJvdGggcG9zaXRpdmUgYW5kIG5lZ2F0aXZlCnZhbHVlczoKCmBgYHtyLCBmaWcud2lkdGggPSAxMCwgd2FybmluZyA9IEZBTFNFLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KY3RzYW1wQyA8LSBtdXRhdGUoY3RzYW1wLCB0ZW1wID0gcm91bmQoKHRlbXAgLSAzMikgLyAxLjgpKQpwMSA8LSBnZ3Bsb3QoY3RzYW1wQywgYWVzKHkgPSBjaXR5LCB4ID0gdGVtcCkpICsKICAgIGdlb21fcG9pbnQoY29sb3IgPSAiZGVlcHNreWJsdWUzIikgKwogICAgZ2VvbV92bGluZSh4aW50ZXJjZXB0ID0gMCwgbHR5ID0gMikgKwogICAgbGFicyh4ID0gIlRlbXBlcmF0dXJlIChkZWdyZWVzIEMpIiwgeSA9IE5VTEwpICsKICAgIHRobQpwMiA8LSBnZ3Bsb3QoY3RzYW1wQywgYWVzKHggPSB0ZW1wLCB5ID0gY2l0eSkpICsKICAgIGdlb21fY29sKGZpbGwgPSAiZGVlcHNreWJsdWUzIikgKwogICAgbGFicyh4ID0gIlRlbXBlcmF0dXJlIChkZWdyZWVzIEMpIiwgeSA9IE5VTEwpICsKICAgIHRobQpsaWJyYXJ5KHBhdGNod29yaykKcDEgKyBwMgpgYGAKClRoaXMgcHV0cyBhIHN0cm9uZyBlbXBoYXNpcyBvbiB0aGUgYmFzZSBsaW5lCgpUaGlzIGNhbiBiZSB1c2VmdWwgaWYgdGhlIGJhc2VsaW5lIGlzIG1lYW5pbmdmdWwsIHN1Y2ggYXMKCiogW2FuIGF2ZXJhZ2UgbGV2ZWxdKGh0dHBzOi8vd3d3Lm5jZWkubm9hYS5nb3YvYWNjZXNzL21vbml0b3JpbmcvY2xpbWF0ZS1hdC1hLWdsYW5jZS9nbG9iYWwvdGltZS1zZXJpZXMvZ2xvYmUvbGFuZF9vY2Vhbi95dGQvMTIvMTg1MC0yMDI0KQogKFthbHRlcm5hdGl2ZV0oYHIgSU1HKCJnbG9iYWwtc3VyZmFjZS10ZW1wZXJhdHVyZS0yMDIyMDYyNC5qcGciKWApKS4KCiogemVybyBkZWdyZWVzIENlbGNpdXMKClplcm8gZGVncmVlcyBGYWhyZW5oZWl0IGlzIG5vdCBtZWFuaW5nZnVsOgoKYGBge3IsIGZpZy53aWR0aCA9IDEwLCB3YXJuaW5nID0gRkFMU0UsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwMSA8LSBnZ3Bsb3QoY3RzYW1wLCBhZXMoeSA9IGNpdHksIHggPSB0ZW1wKSkgKwogICAgZ2VvbV9wb2ludChjb2xvciA9ICJkZWVwc2t5Ymx1ZTMiKSArCiAgICBnZW9tX3ZsaW5lKHhpbnRlcmNlcHQgPSAwLCBsdHkgPSAyKSArCiAgICBsYWJzKHggPSAiVGVtcGVyYXR1cmUgKGRlZ3JlZXMgRikiLCB5ID0gTlVMTCkgKwogICAgdGhtCnAyIDwtIGdncGxvdChjdHNhbXAsIGFlcyh4ID0gdGVtcCwgeSA9IGNpdHkpKSArCiAgICBnZW9tX2NvbChmaWxsID0gImRlZXBza3libHVlMyIpICsKICAgIGxhYnMoeCA9ICJUZW1wZXJhdHVyZSAoZGVncmVlcyBGKSIsIHkgPSBOVUxMKSArCiAgICB0aG0KcDEgKyBwMgpgYGAKCgojIyMgR3JvdXBlZCBCYXIgQ2hhcnRzCgpBIF9ncm91cGVkIGJhciBjaGFydF8gY2FuIGJlIHVzZWQgdG8gc2hvdyB0d28gbWVhc3VyZW1lbnRzLCBlLmcuIGxpZmUKZXhwZWN0YW5jeSB2YWx1ZXMgZm9yIHR3byB5ZWFycy4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGxlMikgKwogICAgZ2VvbV9jb2woYWVzKHggPSBsaWZlRXhwLAogICAgICAgICAgICAgICAgIHkgPSByZW9yZGVyKGNvdW50cnksIGxpZmVFeHApLAogICAgICAgICAgICAgICAgIGZpbGwgPSBZZWFyKSwKICAgICAgICAgICAgIHBvc2l0aW9uID0gImRvZGdlIikgKwogICAgbGFicyh4ID0gIkxpZmUgRXhwZWN0YW5jeSAoeWVhcnMpIiwKICAgICAgICAgeSA9IE5VTEwpICsKICAgIHNjYWxlX3hfY29udGludW91cygKICAgICAgICBleHBhbmQgPSBleHBhbnNpb24obXVsdCA9IGMoMCwgLjEpKSkgKwogICAgdGhtCmBgYAoKVGhpcyB2aXN1YWxpemF0aW9uIHdvdWxkIGJlIG1vcmUgZWZmZWN0aXZlIGZvcgoKKiBmZXdlciBjb3VudHJpZXMgYW5kIG1vcmUgeWVhcnMKCiogd2l0aCBtb3JlIHZhcmlhdGlvbiBpbiByYXRpb3Mgd2l0aGluIGFuZCBiZXR3ZWVuIGNhdGVnb3JpZXMuCgpJbiB0aGlzIGNhc2UgdGhlIGRvdCBwbG90IGlzIGEgbXVjaCBiZXR0ZXIgY2hvaWNlLgoKRm9yIHRoZSBgYmFybGV5YCBkYXRhLCBsb29raW5nIGF0IHRvdGFsIHlpZWxkcyBmb3IgZWFjaCBvZiB0aGUgc2l0ZXMKYW5kIHRoZSB0d28geWVhcnM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiX3RvdCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSB5aWVsZCwgeSA9IHNpdGUsIGZpbGwgPSB5ZWFyKSwKICAgICAgICAgICAgIHBvc2l0aW9uID0gImRvZGdlIikgKwogICAgbGFicyh4ID0gIlRvdGFsIFlpZWxkIChidXNoZWxzL2FjcmUpIiwKICAgICAgICAgeSA9IE5VTEwpICsKICAgIHNjYWxlX3hfY29udGludW91cygKICAgICAgICBleHBhbmQgPSBleHBhbnNpb24obXVsdCA9IGMoMCwgLjEpKSkgKwogICAgdGhtCmBgYAoKCiMjIyBTdGFja2VkIEJhciBDaGFydHMKCkEgX3N0YWNrZWQgYmFyIGNoYXJ0XyBpcyBhcHByb3ByaWF0ZSB3aGVuIGFkZGluZyB0aGUgdmFsdWVzIHdpdGhpbiBhCmNhdGVnb3J5IHRvIGZvcm0gYSB0b3RhbCBtYWtlcyBzZW5zZS4KCkZvciB0aGUgYGJhcmxleWAgZGF0YToKCmBgYHtyLCBmaWcuaGVpZ2h0ID0gNCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdncGxvdChiX3RvdCkgKwogICAgZ2VvbV9jb2woYWVzKHggPSB5aWVsZCwgeSA9IHNpdGUsIGZpbGwgPSB5ZWFyKSwKICAgICAgICAgICAgIHBvc2l0aW9uID0gInN0YWNrIikgKwogICAgbGFicyh4ID0gIlRvdGFsIFlpZWxkIChidXNoZWxzL2FjcmUpIiwKICAgICAgICAgeSA9IE5VTEwpICsKICAgIHNjYWxlX3hfY29udGludW91cygKICAgICAgICBleHBhbmQgPSBleHBhbnNpb24obXVsdCA9IGMoMCwgLjEpKSkgKwogICAgdGhtCmBgYAoKKiBUaGUgY29tYmluZWQgYmFycyBzaG93IHRoZSB0d28teWVhciB0b3RhbHMuCgoqIFRoZSBiYXIgc2VnbWVudHMgc2hvdyB0aGUgY29udHJpYnV0aW9uIG9mIGVhY2ggeWVhciB3aXRoaW4gdGhlIHNpdGVzLgoKKiBDb21wYXJpbmcgMTkzMSB5aWVsZHMgYWNyb3NzIHNpdGVzIGlzIGVhc3k7IGNvbXBhcmluZyAxOTMyIHZhbHVlcyBpcyBoYXJkZXIuCgpBIHN0YWNrZWQgYmFyIGNoYXJ0IHdvdWxkIG1ha2Ugbm8gc2Vuc2UgZm9yIHRoZSB0d28teWVhciBsaWZlCmV4cGVjdGFuY3kgZGF0YS4KCgojIyMgQ2F0ZWdvcnkgT3JkZXIKCk9yZGVyaW5nIG9mIGNhdGVnb3JpZXMgY2FuIGNoYW5nZSB0aGUgdmlzdWFsIGVmZmVjdGl2ZW5lc3Mgb2YgYmFyIGNoYXJ0cy4KCgojIyMjIFN1cGVybWFya2V0IFNhbGVzCgpBIHNtYWxsIGRhdGEgc2V0IG9uIG11bHRpLW5hdGlvbmFsIHN1cGVybWFya2V0IGNoYWluIHNhbGVzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpjaGFpbnMgPC0gcmVhZC5jc3YodGV4dENvbm5lY3Rpb24oIkNoYWluLCBUb3RhbCwgRm9yZWlnbgpXYWxtYXJ0LCAyMiwgNQpDb3N0Y28sIDQuNSwgMgpUZXNjbywgMywgMC41CkNhcnJlZm91ciwgMi41LCAyIikpCmNoYWlucyA8LSBtdXRhdGUoY2hhaW5zLCBIb21lID0gVG90YWwgLSBGb3JlaWduKQp0YmwgPC0gc2VsZWN0KGNoYWlucywgQ2hhaW4sIEhvbWUsIEZvcmVpZ24sIFRvdGFsKQprYmwgPC0ga25pdHI6OmthYmxlKHRibCwgZm9ybWF0ID0gImh0bWwiKQprYWJsZUV4dHJhOjprYWJsZV9zdHlsaW5nKGtibCwgZnVsbF93aWR0aCA9IEZBTFNFKQpgYGAKPCEtLSBodHRwczovL2p1bmtjaGFydHMudHlwZXBhZC5jb20vanVua19jaGFydHMvMjAyMC8wMS90YWtpbmctc21hbGwtc3RlcHMtdG8tYnJpbmctb3V0LXRoZS1tZXNzYWdlLmh0bWwgLS0+CgpUaGUgZGVmYXVsdCBhbHBoYWJldGljYWwgb3JkZXJpbmcgb2YgdGhlIGNoYWlucyBpbiBhIGJhciBjaGFydCBpcyBub3QgaWRlYWw6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxpYnJhcnkodGlkeXIpCmNoYWlucyA8LSBtdXRhdGUoY2hhaW5zLCBUb3RhbCA9IE5VTEwpCmxjaGFpbnMgPC0gcGl2b3RfbG9uZ2VyKGNoYWlucywKICAgICAgICAgICAgICAgICAgICAgICAgLUNoYWluLAogICAgICAgICAgICAgICAgICAgICAgICBuYW1lc190byA9ICJUeXBlIiwKICAgICAgICAgICAgICAgICAgICAgICAgdmFsdWVzX3RvID0gIlNhbGVzIikKcCA8LSBnZ3Bsb3QobGNoYWlucywKICAgICAgICAgICAgYWVzKHggPSBTYWxlcywgeSA9IENoYWluLCBmaWxsID0gVHlwZSkpICsKICAgIGdlb21fY29sKCkgKwogICAgeWxhYihOVUxMKSArCiAgICBzY2FsZV94X2NvbnRpbnVvdXMoCiAgICAgICAgZXhwYW5kID0gZXhwYW5zaW9uKG11bHQgPSBjKDAsIC4xKSkpICsKICAgIHNjYWxlX2ZpbGxfYnJld2VyKAogICAgICAgIHBhbGV0dGUgPSAiUGFpcmVkIiwKICAgICAgICBndWlkZSA9IGd1aWRlX2xlZ2VuZCh0aXRsZSA9IE5VTEwsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgcmV2ZXJzZSA9IFRSVUUpKSArCiAgICB0aG0gKyB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKcApgYGAKClJlb3JkZXJpbmcgYnkgdG90YWwgc2FsZXMgcHJvZHVjZXMgYSBiZXR0ZXIgcmVzdWx0OgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsY2hhaW5fcyA8LQogICAgbXV0YXRlKGxjaGFpbnMsCiAgICAgICAgICAgQ2hhaW4gPSByZW9yZGVyKENoYWluLCBTYWxlcywgRlVOID0gc3VtKSkKcCAlKyUgbGNoYWluX3MKYGBgCgpXaXRoIHRoaXMgb3JkZXJpbmcsIGNvbXBhcmluZyB0aGUgZmlyc3QgY2F0ZWdvcnkgb2Ygc2FsZXMsIGBIb21lYCwKYW1vbmcgY2hhaW5zIGlzIGVhc2llciB0aGFuIGNvbXBhcmluZyB0aGUgYEZvcmVpZ25gIHNhbGVzIGFzIHRoZQpgSG9tZWAgdmFsdWVzIGhhdmUgYSBjb21tb24gYmFzZWxpbmUuCgpJZiB0aGUgZ29hbCBvZiB0aGUgdmlzdWFsaXphdGlvbiBpcyB0byBlbXBoYXNpemUgdGhlIGZvcmVpZ24gc2FsZXMKdGhlbiByZXZlcnNpbmcgdGhlIG9yZGVyIHdvdWxkIGJlIGJldHRlci4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGNoYWluX3N0IDwtCiAgICBtdXRhdGUobGNoYWluX3MsCiAgICAgICAgICAgVHlwZSA9IGZhY3RvcihUeXBlLAogICAgICAgICAgICAgICAgICAgICAgICAgbGV2ZWxzID0gYygiSG9tZSIsICJGb3JlaWduIikpKQpwICUrJSBsY2hhaW5fc3QgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJQYWlyZWQiLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQodGl0bGUgPSBOVUxMLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgcmV2ZXJzZSA9IFRSVUUpLAogICAgICAgICAgICAgICAgICAgICAgZGlyZWN0aW9uID0gLTEpCmBgYAoKVGhpcyBhbHNvIG1ha2VzIGl0IGVhc3kgdG8gc2VlIHRoYXQgV2FsbWFydCdzIGludGVybmF0aW9uYWwgc2FsZXMKYWxvbmUgZXhjZWVkIHRoZSB0b3RhbCBzYWxlcyBvZiBlYWNoIG9mIHRoZSBvdGhlciBjaGFpbnMuCgpBIF9maWxsZWQgYmFyIGNoYXJ0XyBjYW4gYmUgdXNlZCB0byBoZWxwIGNvbXBhcmUgdGhlIHByb3BvcnRpb25zIG9mCnRvdGFsIHNhbGVzIGZyb20gZm9yZWlnbiBzdG9yZXMuCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmxldnMgPC0KICAgIGxldmVscyh3aXRoKGNoYWlucywKICAgICAgICAgICAgICAgIHJlb3JkZXIoQ2hhaW4sIEZvcmVpZ24gLyAoRm9yZWlnbiArIEhvbWUpKSkpCm11dGF0ZShsY2hhaW5fc3QsIENoYWluID0gZmFjdG9yKENoYWluLCBsZXZzKSkgfD4KZ2dwbG90KGFlcyh4ID0gU2FsZXMsIHkgPSBDaGFpbiwgZmlsbCA9IFR5cGUpKSArCiAgICBnZW9tX2NvbChwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgbGFicyh4ID0gIlByb3BvcnRpb24gb2YgU2FsZXMiLCB5ID0gTlVMTCkgKwogICAgc2NhbGVfeF9jb250aW51b3VzKAogICAgICAgIGV4cGFuZCA9IGV4cGFuc2lvbihtdWx0ID0gYygwLCAuMSkpKSArCiAgICBzY2FsZV9maWxsX2JyZXdlcihwYWxldHRlID0gIlBhaXJlZCIsCiAgICAgICAgICAgICAgICAgICAgICBndWlkZSA9IGd1aWRlX2xlZ2VuZCh0aXRsZSA9IE5VTEwsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICByZXZlcnNlID0gVFJVRSksCiAgICAgICAgICAgICAgICAgICAgICBkaXJlY3Rpb24gPSAtMSkgKwogICAgdGhtICsgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpCmBgYApUaGlzIG5vIGxvbmdlciBzaG93cyB0aGUgZGlmZmVyaW5nIHRvdGFsIHNhbGVzLgoKQSBfc3BpbmUgcGxvdF8gc2hvd3MgdGhlIHRvdGFsIHNhbGVzIGJ5IG1hcHBpbmcgdGhlbSB0byB0aGUgYmFyIHdpZHRoczoKCmBgYHtyIHN1cGVybWFya2V0cy1zcGluZXBsb3QsIGVjaG8gPSBGQUxTRX0KIyMgZ2VvbV9jb2woKSBkb2VzIG5vdCBhbGxvdyBgd2lkdGhgIHRvIGJlIHVzZWQgYXMgYW4gYWVzdGhldGljLAojIyBidXQgYSBzcGluZSBwbG90IGNhbiBiZSBwcm9kdWNlZCBieSBjYWxjdWxhdGluZyBiYXIgcG9zaXRpb25zCiMjIGFuZCB3aWR0aHMuIFRoaXMgcmVxdWlyZXMgY3JlYXRpbmcgYSB2ZXJ0aWNhbCBiYXIgY2hhcnQgYW5kCiMjIHVzaW5nIGNvb3JkX2ZsaXAoKS4KZ2FwIDwtIDAuMDIKc3BjaGFpbnMgPC0KICAgIG11dGF0ZShjaGFpbnMsCiAgICAgICAgICAgVG90YWwgPSBIb21lICsgRm9yZWlnbiwKICAgICAgICAgICB0b3QucHJwID0gVG90YWwgLyBzdW0oVG90YWwpLCAgICAgICMjIGJhciB3aWR0aHMKICAgICAgICAgICBzdGFydCA9IGMoMCwgY3Vtc3VtKHRvdC5wcnAgKyBnYXApWy1uKCldKSwKICAgICAgICAgICBlbmQgPSB0b3QucHJwWzFdICsgYygwLCBjdW1zdW0odG90LnBycFstMV0gKyBnYXApKSwKICAgICAgICAgICBtaWQgPSAoc3RhcnQgKyBlbmQpIC8gMikgICAgICAgICAgICMjIGJhciBwb3NpdGlvbnMKCmxzcGNoYWlucyA8LSBwaXZvdF9sb25nZXIoc3BjaGFpbnMsCiAgICAgICAgICAgICAgICAgICAgICAgICAgYyhIb21lLCBGb3JlaWduKSwKICAgICAgICAgICAgICAgICAgICAgICAgICBuYW1lc190byA9ICJUeXBlIiwKICAgICAgICAgICAgICAgICAgICAgICAgICB2YWx1ZXNfdG8gPSAiU2FsZXMiKSB8PgogICAgbXV0YXRlKENoYWluID0gcmVvcmRlcihDaGFpbiwgVG90YWwpKQoKWCA8LSB1bmlxdWUobHNwY2hhaW5zJG1pZCkgICAgICMjIGF4aXMgYnJlYWtzCkMgPC0gdW5pcXVlKGxzcGNoYWlucyRDaGFpbikgICAjIyBheGlzIGJyZWFrIGxhYmVscwpXIDwtIGxzcGNoYWlucyR0b3QucHJwICAgICAgICAgCgpnZ3Bsb3QobHNwY2hhaW5zLCBhZXMoeCA9IG1pZCwgeSA9IFNhbGVzLCBmaWxsID0gVHlwZSkpICsKICAgIGdlb21fY29sKHBvc2l0aW9uID0gImZpbGwiLCB3aWR0aCA9IFcpICsKICAgIHNjYWxlX3hfY29udGludW91cyhicmVha3MgPSBYLCBsYWJlbHMgPSBDKSArCiAgICBsYWJzKHggPSBlbGVtZW50X2JsYW5rKCksIHkgPSAiUHJvcG9ydGlvbiBvZiBTYWxlcyIpICsKICAgIHNjYWxlX3lfY29udGludW91cygKICAgICAgICBleHBhbmQgPSBleHBhbnNpb24obXVsdCA9IGMoMCwgLjEpKSkgKwogICAgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJQYWlyZWQiLAogICAgICAgICAgICAgICAgICAgICAgZ3VpZGUgPSBndWlkZV9sZWdlbmQodGl0bGUgPSBOVUxMLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgcmV2ZXJzZSA9IFRSVUUpLAogICAgICAgICAgICAgICAgICAgICAgZGlyZWN0aW9uID0gLTEpICsKICAgIHRobSArIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJ0b3AiKSArCiAgICBjb29yZF9mbGlwKCkKYGBgCmBgYHtyIHN1cGVybWFya2V0cy1zcGluZXBsb3QsIGV2YWwgPSBGQUxTRSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmBgYAoKCiMjIyMgMjAxNiBFbGVjdGlvbiBSZXN1bHRzCgpBbm90aGVyIGV4YW1wbGUgZm9yIGZpbGxlZCBiYXIgY2hhcnRzIGlzIHByb3ZpZGVkIGJ5IDIwMTYgcHJlc2lkZW50aWFsCmVsZWN0aW9uIHJlc3VsdHMgYnkgc3RhdGUuCgpUaGlzIGlzIHByb2R1Y2VkIGJ5IGRlZmF1bHQgc2V0dGluZ3MuCgpUaGUgdmFsdWVzIGZvciBDbGludG9uIGFyZSBlYXN5IHRvIGNvbXBhcmUsIGFzIHRoZXkgYXJlIG9uIGEgY29tbW9uCmJhc2VsaW5lLgoKVGhlIHZhbHVlcyBmb3IgT3RoZXIgYXJlIGFsc28gb24gYSBjb21tb24gYmFzZWxpbmUsIGJ1dCB0aGUKbnVtYmVycyBmb3IgVHJ1bXAgYXJlIG5vdC4KCmBgYHtyIHByZXMyMDE2LWRmbHQsIGUgPSBGQUxTRSwgZmlnLmhlaWdodCA9IDYuNSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgPC0gZ2dwbG90KGdlb2ZhY2V0OjplbGVjdGlvbiwKICAgICAgICAgICAgYWVzKHggPSB2b3RlcywKICAgICAgICAgICAgICAgIHkgPSBzdGF0ZSwKICAgICAgICAgICAgICAgIGZpbGwgPSBjYW5kaWRhdGUpKSArCiAgICBnZW9tX2NvbChwb3NpdGlvbiA9ICJmaWxsIikgKwogICAgc2NhbGVfeF9jb250aW51b3VzKGV4cGFuZCA9IGMoMCwgMCkpICsKICAgIHhsYWIoTlVMTCkgKwogICAgZ2VvbV92bGluZSh4aW50ZXJjZXB0ID0gMC41LCBsaW5ldHlwZSA9IDIpCnAKYGBgCgpSZW9yZGVyaW5nIHRoZSBjYXRlZ29yaWVzIHB1dHMgYm90aCBDbGludG9uIGFuZCBUcnVtcCBvbiBjb21tb24KYmFzZWxpbmVzIGFuZCBhbHNvIG1hdGNoZXMgdGhlIGNvbW1vbiBjb2xvciB1c2U6CgpgYGB7ciwgZmlnLmhlaWdodCA9IDYuNSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CiMjIG1vdmUgJ090aGVyJyB0byBtaWRkbGUsIGFsaWduIENsaW50b24vVHJ1bXAgd2l0aCBjb2xvcnMKZWxlY3QgPC0KICAgIG11dGF0ZShnZW9mYWNldDo6ZWxlY3Rpb24sCiAgICAgICAgICAgY2FuZGlkYXRlID0gZmFjdG9yKGNhbmRpZGF0ZSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgYygiVHJ1bXAiLCAiT3RoZXIiLCAiQ2xpbnRvbiIpKSkKcCAlKyUgZWxlY3QKYGBgCgpEaWZmZXJlbnQgb3JkZXJpbmdzIG9mIHRoZSBzdGF0ZXMgY2FuIGJlIHVzZWQgdG8gYWNoaWV2ZSBkaWZmZXJlbnQgZ29hbHMuCgpPcmRlcmluZyBieSBDbGludG9uJ3MgcGVyY2VudGFnZSBtYWtlcyBpdCBlYXNpZXIgdG8gc2VlIHdoZXJlIHNoZSBoYWQKYW4gb3V0cmlnaHQgbWFqb3JpdHkuCgpgYGB7ciwgZmlnLmhlaWdodCA9IDYuNSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmVsZWN0X3dpZGUgPC0gcGl2b3Rfd2lkZXIoc2VsZWN0KGVsZWN0LCAtdm90ZXMpLAogICAgICAgICAgICAgICAgICAgICAgICAgIG5hbWVzX2Zyb20gPSBjYW5kaWRhdGUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgdmFsdWVzX2Zyb20gPSBwY3QpCgojIyBvcmRlcmVkIGJ5IENsaW50b24gcGN0CnNsZXZzIDwtIGFycmFuZ2UoZWxlY3Rfd2lkZSwgQ2xpbnRvbikgfD4KICAgIHB1bGwoc3RhdGUpCnAgJSslIG11dGF0ZShlbGVjdCwgc3RhdGUgPSBmYWN0b3Ioc3RhdGUsIHNsZXZzKSkKYGBgCgpBbm90aGVyIHBvc3NpYmlsaXR5IGlzIHRvIG9yZGVyIGJ5IHdpbm5pbmcgbWFyZ2luIGJldHdlZW4gdGhlIHR3bwptYWpvciBjYW5kaWRhdGVzLgoKYGBge3IsIGZpZy5oZWlnaHQgPSA2LjUsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQojIyBvcmRlcmVkIGJ5IHdpbm5pbmcgbWFyZ2luCnNsZXZzIDwtIGFycmFuZ2UoZWxlY3Rfd2lkZSwgQ2xpbnRvbiAtIFRydW1wKSB8PgogICAgcHVsbChzdGF0ZSkKcCAlKyUgbXV0YXRlKGVsZWN0LCBzdGF0ZSA9IGZhY3RvcihzdGF0ZSwgc2xldnMpKQpgYGAKCgojIyBGYWNldGluZwoKRmFjZXRpbmcgY2FuIGJlIHVzZWQgd2l0aCBkb3QgcGxvdHMgYW5kIGJhciBjaGFydHMgYXMgd2VsbDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGJhcmxleSkgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IHlpZWxkLAogICAgICAgICAgICAgICAgICAgeSA9IHZhcmlldHksCiAgICAgICAgICAgICAgICAgICBjb2xvciA9IHllYXIpKSArCiAgICBmYWNldF93cmFwKH4gc2l0ZSkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpCmBgYAoKVGhpcyB2aWV3IG9mIHRoZSBgYmFybGV5YCBkYXRhIHNob3dzIGxvd2VyIHlpZWxkcyBmb3IgMTkzMiB0aGFuIGZvciAxOTMxCmZvciBhbGwgc2l0ZXMgZXhjZXB0IE1vcnJpcy4KCiogQ2xldmVsYW5kIHN1Z2dlc3QgdGhpcyBtYXkgaW5kaWNhdGUgYSBkYXRhIGVudHJ5IGVycm9yIGZvciBNb3JyaXMuCgoqIEEgW3BhcGVyIGZyb20KMjAxNF0oaHR0cHM6Ly9ibG9nLnJldm9sdXRpb25hbmFseXRpY3MuY29tLzIwMTQvMDcvdGhlcmVzLW5vLW1pc3Rha2UtaW4tdGhlLWJhcmxleS1kYXRhLmh0bWwpCnN1Z2dlc3RzIHRoZXJlIG1heSBiZSBubyBlcnJvci4KCgojIyBIZWF0IE1hcHMKCkhlYXQgbWFwcyBlbmNvZGUgYSBudW1lcmljIHZhcmlhYmxlIGFzIHRoZSBjb2xvciBvZiBhIHRpbGUgcGxhY2VkIGF0IGEKcGFydGljdWxhciBwb3NpdGlvbiBpbiBhIGdyaWQuCgpIZWF0IG1hcHMgYXJlIGFsc28gY2FsbGVkIF9tYXRyaXggY2hhcnRzXyBvciBfaW1hZ2UgcGxvdHNfLgoKSGVhdCBtYXBzIGNhbiBiZSBlZmZlY3RpdmUgaW4gY2FzZXMgd2hlcmUgYSBsaW5lIHBsb3QgY29udGFpbnMgdG9vCm11Y2ggb3Zlci1wb3R0aW5nLCBzdWNoIGFzCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmdtYSA8LSBmaWx0ZXIoZ2FwbWluZGVyLCBjb250aW5lbnQgPT0gIkFtZXJpY2FzIikKZ2dwbG90KGdtYSkgKwogICAgZ2VvbV9saW5lKGFlcyh4ID0geWVhciwKICAgICAgICAgICAgICAgICAgeSA9IGxpZmVFeHAsCiAgICAgICAgICAgICAgICAgIGNvbG9yID0gY291bnRyeSkpICsKICAgIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJ0b3AiLAogICAgICAgICAgbGVnZW5kLnRpdGxlID0gZWxlbWVudF9ibGFuaygpKQpgYGAKCkEgaGVhdCBtYXAgb2YgdGhlc2UgZGF0YToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGdtYSkgKwogICAgZ2VvbV90aWxlKGFlcyh4ID0geWVhciwKICAgICAgICAgICAgICAgICAgeSA9IHJlb3JkZXIoY291bnRyeSwgbGlmZUV4cCksCiAgICAgICAgICAgICAgICAgIGZpbGwgPSBsaWZlRXhwKSkgKwogICAgc2NhbGVfeF9jb250aW51b3VzKGV4cGFuZCA9IGMoMCwgMCkpICsKICAgIHNjYWxlX2ZpbGxfdmlyaWRpc19jKCkgKwogICAgbGFicyh5ID0gTlVMTCwKICAgICAgICAgZmlsbCA9ICJMaWZlIEV4cGVjdGFuY3kgKHllYXJzKSIpICsKICAgIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJ0b3AiKQpgYGAKCkFnYWluIGl0IGlzIHVzZWZ1bCB0byBjb25zaWRlciByZW9yZGVyaW5nIG9mIGNhdGVnb3JpZXMgd2hlbiB0aGVyZSBpcwpubyBuYXR1cmFsIG9yZGVyLgoKVGhpcyBoZWF0IG1hcCBvcmRlcnMgdGhlIGNvdW50cmllcyBieSBhdmVyYWdlIGxpZmUgZXhwZWN0YW5jeS4KCgojIyBCdWJibGUgQ2hhcnRzCgpBIGZvcm0gb2YgY2hhcnQgb2Z0ZW4gc2VlbiBpbiB0aGUgcG9wdWxhciBwcmVzcyBpcyB0aGUgX2J1YmJsZSBjaGFydF8uCgpUaGUgYnViYmxlIGNoYXJ0IHVzZXMgYXJlcyBvZiBjaXJjbGVzIHRvIHJlcHJlc2VudCBtYWduaXR1ZGVzLgoKUG9zaXRpb24gaW4gdGhlIHBsYW5lIGlzIHVzdWFsbHkgbm90IGZ1bGx5IHVzZWQgb3Igbm90IHVzZWQgYXQgYWxsIGZvcgptYXBwaW5nIGF0dHJpYnV0ZXMuCgpJbiBvbi1saW5lIHB1YmxpY2F0aW9ucyBmdXJ0aGVyIGluZm9ybWF0aW9uIG9uIGVhY2ggb2YgdGhlIGJ1YmJsZXMgaXMKb2Z0ZW4gcHJvdmlkZWQgdGhyb3VnaCBpbnRlcmFjdGlvbnMsIHN1Y2ggYXMgYSBtb3VzZS1vdmVyIHRvb2x0aXAuCgpPdGhlciBjaGFydHMgZm9ybXMgYXJlIGFsbW9zdCBhbHdheXMgYmV0dGVyIGZvciBlbmNvZGluZyB0aGUgbWFnbml0dWRlCmluZm9ybWF0aW9uLgoKSXQgaXMgYWxzbyBlYXN5IHRvIGdldCB0aGUgZW5jb2Rpbmcgd3JvbmcKKFtDb3JyZWN0ZWQgdmVyc2lvbl0oYHIgSU1HKCJzaHJpbmtpbmctYmFua3MtY29ycmVjdC5qcGciKWApKToKCmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI2MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoInNocmlua2luZy1iYW5rcy1vcmlnLmpwZyIpKQpgYGAKCjwhLS0KICBodHRwOi8vd3d3LnBlcmNlcHR1YWxlZGdlLmNvbS9ibG9nLz9wPTE1MzIKICAhW10oaHR0cDovL3d3dy5wZXJjZXB0dWFsZWRnZS5jb20vYmxvZy93cC1jb250ZW50L3VwbG9hZHMvMjAxMy8wMy9zaG93LW1lLWJ1YmJsZXMucG5nKQogIGh0dHA6Ly9qdW5rY2hhcnRzLnR5cGVwYWQuY29tL2p1bmtfY2hhcnRzLzIwMDkvMDEvcG9wcGluZy10aGUtYnViYmxlLXNvLXRvLXNwZWFrLmh0bWwKICBodHRwczovL2ZsaXBjaGFydGZhaXJ5dGFsZXMuZmlsZXMud29yZHByZXNzLmNvbS8yMDA5LzAxL2JhbmtzMjBtYXJrZXQyMGNhcDIwY29ycmVjdDEuanBnCiAgLS0+CgpgZ2dwbG90YCBidWJibGUgY2hhcnRzIGZvciB0aGUgYXZlcmFnZSBgeWllbGRgIHZhbHVlcyBmcm9tIHRoZSBgYmFybGV5YApkYXRhIGFuZCBmb3IgdGhlIDIwMDcgcG9wdWxhdGlvbiBzaXplcyBmb3IgdGhlIGdhcG1pbmRlciBkYXRhOgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgbWVzc2FnZSA9IEZBTFNFLCBmaWcud2lkdGggPSAxMH0KIyMgZGVyaXZlZCBmcm9tCiMjIGh0dHA6Ly9zdGFja292ZXJmbG93LmNvbS9xdWVzdGlvbnMvMzg5NTkwOTMvcGFja2VkLWJ1YmJsZS1waWUtY2hhcnRzLWluLXIKbGlicmFyeShwYWNrY2lyY2xlcykKY2lyY2xlcyA8LSBmdW5jdGlvbihyYWQyKSB7CiAgICBzdG9waWZub3QoYWxsKHJhZDIgPiAwKSkKICAgIHJhZCA8LSBzcXJ0KHJhZDIpCiAgICBuIDwtIGxlbmd0aChyYWQpCiAgICBsaW0gPC0gbiAqIG1heChyYWQpCiAgICBsaW1zIDwtIGMoLWxpbSwgbGltKQogICAgb2xkLnNlZWQgPC0geyBydW5pZigxKTsgLlJhbmRvbS5zZWVkIH0gIyBub2xpbnQKICAgIHNldC5zZWVkKDEyMzQ1KQogICAgdiA8LSBjaXJjbGVMYXlvdXQoY2JpbmQocnVuaWYobiksIHJ1bmlmKG4pLCByYWQpLCBsaW1zLCBsaW1zKQogICAgLlJhbmRvbS5zZWVkIDwtIG9sZC5zZWVkCiAgICBsYXlvdXRERiA8LSBhcy5kYXRhLmZyYW1lKHYkbGF5b3V0KQogICAgbmFtZXMobGF5b3V0REYpIDwtIGMoIngiLCAieSIsICJyYWRpdXMiKQogICAgbGlzdChsYXlvdXQgPSBsYXlvdXRERiwgZGF0YSA9IGNpcmNsZVBsb3REYXRhKHYkbGF5b3V0KSkKfQpidWJibGVfdGhlbWUgPC0gZnVuY3Rpb24oKSB7CiAgICBsaXN0KGNvb3JkX2VxdWFsKCksCiAgICB0aGVtZV9idygpLAogICAgdGhlbWUoYXhpcy50ZXh0ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgYXhpcy50aWNrcyA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGl0bGUgPSBlbGVtZW50X2JsYW5rKCkpKQp9CgojIyBiYXJsZXkgeWllbGRzCmFic3kgPC0gZ3JvdXBfYnkoYmFybGV5LCBzaXRlLCB5ZWFyKSB8PgogICAgc3VtbWFyaXNlKGF2Z195aWVsZCA9IG1lYW4oeWllbGQpKQoKdiA8LSBjaXJjbGVzKGFic3kkYXZnX3lpZWxkKQp2diA8LSB2JGRhdGEKdnYkeWVhciA8LSBhYnN5JHllYXJbdnYkaWRdCnAxIDwtIGdncGxvdCh2dikgKwogICAgZ2VvbV9wb2x5Z29uKGFlcyh4LCB5LCBncm91cCA9IGlkLCBmaWxsID0geWVhcikpICsKICAgIGdlb21fdGV4dChhZXMoeCA9IHgsIHkgPSB5LCBsYWJlbCA9IGFic3kkc2l0ZSksCiAgICAgICAgICAgICAgZGF0YSA9IHYkbGF5b3V0LCBzaXplID0gMS41KSArCiAgICBidWJibGVfdGhlbWUoKQoKIyMgZ2FwbWluZGVyIHBvcHVsYXRpb25zIGZvciAyMDA3OgpsaWJyYXJ5KGdhcG1pbmRlcikKbGlicmFyeShwYXRjaHdvcmspCmdtMjAwNyA8LSBmaWx0ZXIoZ2FwbWluZGVyLCB5ZWFyID09IDIwMDcpCnYgPC0gY2lyY2xlcyhnbTIwMDckcG9wKQp2diA8LSB2JGRhdGEKdnYkY29udGluZW50IDwtIGdtMjAwNyRjb250aW5lbnRbdnYkaWRdCnAyIDwtIGdncGxvdCh2dikgKwogICAgZ2VvbV9wb2x5Z29uKGFlcyh4LCB5LCBncm91cCA9IGlkLCBmaWxsID0gY29udGluZW50KSkgKyBjb29yZF9lcXVhbCgpICsKICAgIGJ1YmJsZV90aGVtZSgpCgojI2dyaWQuYXJyYW5nZShwMSwgcDIsIG5yb3cgPSAxKQpwMSArIHAyCmBgYAoKCiMjIFdhdGVyZmFsbCBDaGFydHMKCkFsc28gY2FsbGVkIF9jYXNjYWRlIGNoYXJ0c18uCgpUaGVzZSB1c3VhbGx5IHNob3cgdGhlIGRlY29tcG9zaXRpb24gb2YgYSB0b3RhbCBpbnRvIHBvc2l0aXZlIGFuZApuZWdhdGl2ZSBjb250cmlidXRpb25zIGZyb20gdmFyaW91cyBzb3VyY2VzLgoKPCEtLSBGaWcgNi43IGZyb20gQW5keSBLaXJrJ3MgX0RhdGEgVmlzdWFsaXphdGlvbiwgMm5kIEVkLl8gLS0+CgpOZXcgWmVhbGFuZCBuZXQgaW1taWdyYXRpb24gYnkgcmVnaW9uOgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjcwJSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiNi43LldhdGVyZmFsbC5wbmciKSkKYGBgCgpJbnRlcm5ldCBzdWJzY3JpYmVycyBieSBtb250aCAoW2Jsb2cgcG9zdCB3aXRoIGBnZ3Bsb3RgCmNvZGVdKGh0dHBzOi8vd2ViLmFyY2hpdmUub3JnL3dlYi8yMDE5MDYyMjIxMTkzOC9odHRwOi8vYW5oaG9hbmdkdWMuY29tL2Jsb2cvY3JlYXRlLXdhdGVyZmFsbC1jaGFydC13aXRoLWdncGxvdDIvKSkuCgpgYGB7ciwgZWNobyA9IEZBTFNFLCBvdXQud2lkdGggPSAiNjUlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJ3YXRlcmZhbGwucG5nIikpCmBgYAogIAoKCiMjIFBvbGFyIEFyZWEgQ2hhcnRzCgpGbG9yZW5jZSBOaWdodGluZ2FsZSdzIGZhbW91cyBjaGFydCBzaG93aW5nIHRoZSBlZmZlY3Qgb2YgdGhlCnNhbml0YXRpb24gaW1wcm92ZW1lbnRzIGluIE1hcmNoL0FwcmlsIDE4NTU6Cgo8IS0tIGh0dHBzOi8vdW5kZXJzdGFuZGluZ3VuY2VydGFpbnR5Lm9yZy9maWxlcy9Db3hjb21icy5qcGcgLS0+CmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI5NSUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoIkNveGNvbWJzLmpwZyIpKQpgYGAKClRoaXMgY2hhcnQgaGFzIGJlZW4gY2FsbGVkIGEgX3BvbGFyIGFyZWEgZGlhZ3JhbXNfIG9yIGEgX0NveGNvbWIKQ2hhcnRfLgoKSXQgY2FuIGJlIHZpZXdlZCBhcwoKKiBhIGJhciBjaGFydCB3aXRoIHRoZSBiYXJzIHBvc2l0aW9uZWQgaW4gZnJvbnQgb2YgZWFjaCBvdGhlciwKCiogdHJhbnNmb3JtZWQgdG8gcG9sYXIgY29vcmRpbmF0ZXMsCgoqIHdpdGggbWFnbml0dWRlIG1hcHBlZCB0byBhcmVhIChpLmUuIHNxdWFyZSByb290IG9mIG1hZ25pdHVkZQogIG1hcHBlZCB0byByYWRpdXMpLgoKVGhlIGRhdGEgYXJlIGF2YWlsYWJsZSBpbiB0aGUgYEhpc3REYXRhYCBwYWNrYWdlIGFzIGRhdGEgZnJhbWUgYE5pZ2h0aW5nYWxlYC4KClNvbWUgcmVhcnJhbmdlbWVudCBvZiB0aGUgZGF0YSBpcyBuZWVkZWQgdG8gZ2V0IGl0IGludG8gYSBmb3JtCmFtZW5hYmxlIGZvciBwbG90dGluZy4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShmb3JjYXRzKQpkYXRhKE5pZ2h0aW5nYWxlLCBwYWNrYWdlID0gIkhpc3REYXRhIikKTmlnaHQgPC0KICAgIG11dGF0ZShOaWdodGluZ2FsZSwKICAgICAgICAgICBQZXJpb2QgPQogICAgICAgICAgICAgICBpZmVsc2UoRGF0ZSA8IGFzLkRhdGUoIjE4NTUtMDQtMDEiKSwKICAgICAgICAgICAgICAgICAgICAgICJCZWZvcmUiLAogICAgICAgICAgICAgICAgICAgICAgIkFmdGVyIiksCiAgICAgICAgICAgUGVyaW9kID0KICAgICAgICAgICAgICAgZmFjdG9yKFBlcmlvZCwgYygiQmVmb3JlIiwgIkFmdGVyIikpLAogICAgICAgICAgIE1vbnRoID0gZmFjdG9yKE1vbnRoLCBtb250aC5hYmIpKSB8PgogICAgc2VsZWN0KERhdGUsIE1vbnRoLCBZZWFyLCBQZXJpb2QsCiAgICAgICAgICAgRGlzZWFzZSwgV291bmRzLCBPdGhlcikgfD4KICAgIHBpdm90X2xvbmdlcig1IDogNywKICAgICAgICAgICAgICAgICBuYW1lc190byA9ICJDYXVzZSIsCiAgICAgICAgICAgICAgICAgdmFsdWVzX3RvID0gIkRlYXRocyIpCgojIyBSZWFycmFuZ2UgdGhlIE1vbnRoIGxldmVscyB0byBzdGFydCB3aXRoIEFwcmlsLgpOaWdodDMgPC0gbXV0YXRlKE5pZ2h0LCBNb250aCA9IGZjdF9zaGlmdChNb250aCwgMykpCmBgYAoKQSBzdGFuZGFyZCBzdGFja2VkIGJhciBjaGFydCBvZiB0aGUgZGF0YToKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KE5pZ2h0MywKICAgICAgIGFlcyh4ID0gTW9udGgsIHkgPSBEZWF0aHMsIGZpbGwgPSBDYXVzZSkpICsKICAgIGdlb21fY29sKCkgKwogICAgZmFjZXRfd3JhcCh+IFBlcmlvZCkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpCmBgYAoKQSBncm91cGVkIGJhciBjaGFydCBvZiB0aGUgZGF0YToKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KE5pZ2h0MywKICAgICAgIGFlcyh4ID0gTW9udGgsIHkgPSBEZWF0aHMsIGZpbGwgPSBDYXVzZSkpICsKICAgIGdlb21fY29sKHBvc2l0aW9uID0gImRvZGdlIikgKwogICAgZmFjZXRfd3JhcCh+IFBlcmlvZCkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpCmBgYAoKVXNpbmcgYHBvc2l0aW9uID0gImlkZW50aXR5ImAgdGhlIGJhcnMgd2lsbCBiZSBwbGFjZWQgaW4gZnJvbnQgb2YgZWFjaCBvdGhlcgpyYXRoZXIgdGhhbiBzaWRlIGJ5IHNpZGUgb3Igc3RhY2tlZC4KCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcCA8LSBnZ3Bsb3QoTmlnaHQzLAogICAgICAgICAgICBhZXMoeCA9IE1vbnRoLCB5ID0gRGVhdGhzLCBmaWxsID0gQ2F1c2UpKSArCiAgICBnZW9tX2NvbChwb3NpdGlvbiA9ICJpZGVudGl0eSIsICMjIGJhcnMgaW4gZnJvbnQgb2YgZWFjaCBvdGhlcgogICAgICAgICAgICAgd2lkdGggPSAxLCAgICAgICAgICAgICAjIyByZW1vdmUgc3BhY2UgYmV0d2VlbiBiYXJzCiAgICAgICAgICAgICBjb2xvciA9ICJibGFjayIsICAgICAgICMjIGJhciBib3JkZXIgY29sb3IKICAgICAgICAgICAgIGxpbmV3aWR0aCA9IDAuMSkgKyAgICAgIyMgYmFyIGJvcmRlciB0aGlja25lc3MKICAgIGZhY2V0X3dyYXAofiBQZXJpb2QpICsKICAgIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJ0b3AiKQpwCmBgYAoKUHJvYmxlbTogTGFyZ2VyIGJhcnMgbWF5IGJlIHBsYWNlZCBpbiBmcm9udCBvZiBzbWFsbGVyIG9uZXMuCgpSZW9yZGVyaW5nIHRoZSBgRGVhdGhzYCB2YWx1ZXMgZnJvbSBsYXJnZXN0IHRvIHNtYWxsZXN0IGVuc3VyZXMgdGhhdApsYXJnZXIgYmFycyBkbyBub3QgY292ZXIgc21hbGxlciBvbmVzLgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwIDwtIGdncGxvdChhcnJhbmdlKE5pZ2h0MywgZGVzYyhEZWF0aHMpKSwKICAgICAgICAgICAgYWVzKHggPSBNb250aCwgeSA9IERlYXRocywgZmlsbCA9IENhdXNlKSkgKwogICAgZ2VvbV9jb2wocG9zaXRpb24gPSAiaWRlbnRpdHkiLCAjIyBiYXJzIGluIGZyb250IG9mIGVhY2ggb3RoZXIKICAgICAgICAgICAgIHdpZHRoID0gMSwgICAgICAgICAgICAgIyMgcmVtb3ZlIHNwYWNlIGJldHdlZW4gYmFycwogICAgICAgICAgICAgY29sb3IgPSAiYmxhY2siLCAgICAgICAjIyBiYXIgYm9yZGVyIGNvbG9yCiAgICAgICAgICAgICBsaW5ld2lkdGggPSAwLjEpICsgICAgICMjIGJhciBib3JkZXIgdGhpY2tuZXNzCiAgICBmYWNldF93cmFwKH4gUGVyaW9kKSArCiAgICB0aGVtZShsZWdlbmQucG9zaXRpb24gPSAidG9wIikKcApgYGAKCkNoYW5naW5nIHRvIHBvbGFyIGNvb3JkaW5hdGVzIGFuZCBtYXBwaW5nIHNxdWFyZSByb290cyBvZiBgRGVhdGhzYCB0bwpyYWRpdXMgcHJvZHVjZXMgdGhlIGJhc2ljIHBvbGFyIGFyZWEgY2hhcnQ6CgpgYGB7ciwgZmlnLndpZHRoID0gOCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAgJSslIChhcnJhbmdlKE5pZ2h0MywgZGVzYyhEZWF0aHMpKSB8PgogICAgICAgbXV0YXRlKERlYXRocyA9IHNxcnQoRGVhdGhzKSkpICsKICAgIGNvb3JkX3BvbGFyKCkKYGBgCgpTb21lIGFkanVzdG1lbnRzIGJyaW5nIHRoZSByZXN1bHQgY2xvc2VyIHRvIHRoZSBvcmlnaW5hbDoKCmBgYHtyLCBmaWcud2lkdGggPSA4fQpwICUrJQogICAgKGFycmFuZ2UoTmlnaHQsIGRlc2MoRGVhdGhzKSkgfD4KICAgICBtdXRhdGUoTW9udGggPSBmY3Rfc2hpZnQoTW9udGgsIDYpLAogICAgICAgICAgICBQZXJpb2QgPSBmYWN0b3IoUGVyaW9kLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgYygiQWZ0ZXIiLCAiQmVmb3JlIikpLAogICAgICAgICAgICBEZWF0aHMgPSBzcXJ0KERlYXRocykpKSArCiAgICBjb29yZF9wb2xhcigpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKAogICAgICAgIHZhbHVlcyA9IGMoV291bmRzID0gInBpbmsiLAogICAgICAgICAgICAgICAgICAgT3RoZXIgPSAiZGFya2dyYXkiLAogICAgICAgICAgICAgICAgICAgRGlzZWFzZSA9ICJsaWdodGJsdWUiKSkgKwogICAgdGhlbWUoYXhpcy50aXRsZSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGV4dC55ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgYXhpcy50aWNrcyA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIHBhbmVsLmdyaWQubWFqb3IgPSBlbGVtZW50X2JsYW5rKCksCiAgICAgICAgICBwYW5lbC5ncmlkLm1pbm9yID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgcGFuZWwuYm9yZGVyID0gZWxlbWVudF9ibGFuaygpKQpgYGAKCgojIyBCYXNlIGFuZCBMYXR0aWNlIEdyYXBoaWNzCgpCYXNlIGdyYXBoaWNzIHByb3ZpZGVzIHRoZSBgZG90Y2hhcnQoKWAgZnVuY3Rpb24gZm9yIGNyZWF0aW5nIGRvdCBwbG90czoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0Kd2l0aChsZV9hbV8yMDA3LAogICAgIGRvdGNoYXJ0KHNvcnQobGlmZUV4cCksCiAgICAgICAgICAgICAgbGFiZWxzID0gY291bnRyeVtvcmRlcihsaWZlRXhwKV0pKQpgYGAKClRoZSBgbGF0dGljZWAgcGFja2FnZSBwcm92aWRlcyBgZG90cGxvdCgpYDoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsaWJyYXJ5KGxhdHRpY2UpCmRvdHBsb3QocmVvcmRlcihjb3VudHJ5LCBsaWZlRXhwKSB+IGxpZmVFeHAsCiAgICAgICAgZGF0YSA9IGxlX2FtXzIwMDcpCmBgYAoKTW9zdCBsYXR0aWNlIHBsb3RzIHN1cHBvcnQgYSBgZ3JvdXBgIGFyZ3VtZW50IHRoYXQgaXMgdXN1YWxseSBtYXBwZWQKdG8gY29sb3I6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmRvdHBsb3QocmVvcmRlcihjb3VudHJ5LCBsaWZlRXhwKSB+IGxpZmVFeHAsCiAgICAgICAgZ3JvdXAgPSB5ZWFyLCBkYXRhID0gbGUyLCBhdXRvLmtleSA9IFRSVUUpCmBgYAoKQ3JlYXRpbmcgYSBiYXNpYyBiYXIgY2hhcnQgaW4gYGxhdHRpY2VgIHVzZXMgdGhlIGBiYXJjaGFydCgpYCBmdW5jdGlvbi4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KIyMgQnkgZGVmYXVsdCBsYXR0aWNlIGNyZWF0ZXMgYSBiYWQgYmFyIGNoYXJ0IHdpdGggYQojIyBub24temVybyBiYXNlIGxpbmUgZm9yIHRoZXNlIGRhdGEuIEZpeCB0aGF0IGJ5CiMjIHNwZWNpZnlpbmcgeGxpbSA9IGMoMCwgODUpLgpiYXJjaGFydChyZW9yZGVyKGNvdW50cnksIGxpZmVFeHApIH4gbGlmZUV4cCwKICAgICAgICAgZGF0YSA9IGxlX2FtXzIwMDcsIHhsaW0gPSBjKDAsIDg1KSkKYGBgCgpCYXNlIGdyYXBoaWNzIGFsc28gcHJvdmlkZXMgYSBiYXIgY2hhcnQgd2l0aCB0aGUgYGJhcnBsb3QoKWAgZnVuY3Rpb24uCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnBhcihtYXIgPSBjKDUsIDUsIDQsIDIpICsgMC4xKQp3aXRoKGxlX2FtXzIwMDcsCiAgICAgYmFycGxvdChzb3J0KGxpZmVFeHApLAogICAgICAgICAgICAgaG9yaXogPSBUUlVFLAogICAgICAgICAgICAgbmFtZXMuYXJnID0gY291bnRyeVtvcmRlcihsaWZlRXhwKV0sCiAgICAgICAgICAgICBsYXMgPSAxLAogICAgICAgICAgICAgY2V4Lm5hbWVzID0gMC43LAogICAgICAgICAgICAgY2V4LmF4aXMgPSAwLjcpKQpgYGAKCgojIyBSZWFkaW5nCgpDaGFwdGVyIFtfVmlzdWFsaXppbmcKICBhbW91bnRzX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6L3Zpc3VhbGl6aW5nLWFtb3VudHMuaHRtbCkKICBpbiBbX0Z1bmRhbWVudGFscyBvZiBEYXRhCiAgVmlzdWFsaXphdGlvbl9dKGh0dHBzOi8vY2xhdXN3aWxrZS5jb20vZGF0YXZpei8pLgoKCiMjIEludGVyYWN0aXZlIFR1dG9yaWFsCgpBbiBpbnRlcmFjdGl2ZSBbYGxlYXJucmBdKGh0dHBzOi8vcnN0dWRpby5naXRodWIuaW8vbGVhcm5yLykgdHV0b3JpYWwKZm9yIHRoZXNlIG5vdGVzIGlzIFthdmFpbGFibGVdKGByIFdMTksoInR1dG9yaWFscy9hbW91bnRzLlJtZCIpYCkuCgpZb3UgY2FuIHJ1biB0aGUgdHV0b3JpYWwgd2l0aAoKYGBge3IsIGV2YWwgPSBGQUxTRX0KU1RBVDQ1ODA6OnJ1blR1dG9yaWFsKCJhbW91bnRzIikKYGBgCgpZb3UgY2FuIGluc3RhbGwgdGhlIGN1cnJlbnQgdmVyc2lvbiBvZiB0aGUgYFNUQVQ0NTgwYCBwYWNrYWdlIHdpdGgKCmBgYHtyLCBldmFsID0gRkFMU0V9CnJlbW90ZXM6Omluc3RhbGxfZ2l0bGFiKCJsdWtlLXRpZXJuZXkvU1RBVDQ1ODAiKQpgYGAKCllvdSBtYXkgbmVlZCB0byBpbnN0YWxsIHRoZSBgcmVtb3Rlc2AgcGFja2FnZSBmcm9tIENSQU4gZmlyc3QuCgoKIyMgRXhlcmNpc2VzCgoxLiBBIHBsb3Qgc2ltaWxhciB0byB0aGlzIHdhcyBmZWF0dXJlZCBpbiBhIENOTiBuZXdzIHN0b3J5IHNldmVyYWwgeWVhcnMgYWdvOgoKICAgIGBgYHtyLCBlY2hvID0gRkFMU0V9CiAgICBsaWJyYXJ5KGdncGxvdDIpCiAgICBsZXZzIDwtIGMoIkRlbW9jcmF0cyIsICJSZXB1YmljYW5zIiwgIkluZGVwZW5kZW50cyIpCiAgICBkIDwtIGRhdGEuZnJhbWUocGFydHkgPSBmYWN0b3IobGV2cywgbGV2cyksCiAgICAgICAgICAgICAgICAgICAgcGN0ID0gYyg2MiwgNTQsIDU0KSkKCiAgICBnZ3Bsb3QoZCwgYWVzKHggPSBwYXJ0eSwgeSA9IHBjdCAtIDUwKSkgKwogICAgICAgIGdlb21fY29sKHdpZHRoID0gMC41KSArCiAgICAgICAgc2NhbGVfeV9jb250aW51b3VzKGxhYmVscyA9IHNlcSg1MCwgNjQsIGJ5ID0gMiksCiAgICAgICAgICAgICAgICAgICAgICAgICAgIGJyZWFrcyA9IHNlcSgwLCAxNCwgYnkgPSAyKSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgZXhwYW5kID0gZXhwYW5zaW9uKGMoMCwgMC4xOCkpKSArCiAgICAgICAgbGFicyh4ID0gIlBvbGl0aWNhbCBQYXJ0eSIsCiAgICAgICAgICAgICB5ID0gTlVMTCwKICAgICAgICAgICAgIHRpdGxlID0gIlBlcmNlbnQgV2hvIEFncmVlZCBXaXRoIENvdXJ0IikgKwogICAgICAgIHRoZW1lKHRleHQgPSBlbGVtZW50X3RleHQoc2l6ZSA9IDIwLCBmYWNlID0gImJvbGQiKSwKICAgICAgICAgICAgICBwYW5lbC5ncmlkLm1pbm9yLnggPSBlbGVtZW50X2JsYW5rKCksCiAgICAgICAgICAgICAgcGFuZWwuZ3JpZC5tYWpvci54ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgICAgIHBhbmVsLmdyaWQubWlub3IueSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgICAgICBwYW5lbC5ncmlkLm1ham9yLnkgPSBlbGVtZW50X2xpbmUoY29sb3IgPSAiYmxhY2siKSwKICAgICAgICAgICAgICBwYW5lbC5iYWNrZ3JvdW5kID0gZWxlbWVudF9yZWN0KGZpbGwgPSAiZ3JleSIsIGNvbG9yID0gTkEpLAogICAgICAgICAgICAgIHBsb3QuYmFja2dyb3VuZCA9IGVsZW1lbnRfcmVjdChmaWxsID0gIndoaXRlIiwgY29sb3IgPSAiYmxhY2siLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBsaW5ld2lkdGggPSAyKSwKICAgICAgICAgICAgICBwbG90Lm1hcmdpbiA9IG1hcmdpbigyMCwgMjAsIDIwLCAyMCkpICsKICAgICAgICBjb29yZF9maXhlZCgwLjEpCiAgICBgYGAKCiAgICBXaGljaCBvZiB0aGUgZm9sbG93aW5nIGlzIGFwcHJveGltYXRlbHkgY29ycmVjdDoKICAgIAogICAgLSBBYm91dCB0aGUgc2FtZSBudW1iZXIgb2YgZGVtb2NyYXRzIGFzIHJlcHVibGljYW5zIGFncmVlZCB3aXRoCiAgICAgIHRoZSBjb3VydC4KICAgIC0gQWJvdXQgMTUlIG1vcmUgZGVtb2NyYXRzIHRoYW4gcmVwdWJsaWNhbnMgYWdyZWVkIHdpdGggdGhlIGNvdXJ0LgogICAgLSBBYm91dCB0cmVlIHRpbWVzIGFzIG1hbnkgZGVtb2NyYXRzIHRoYW4gcmVwdWJsaWNhbnMgYWdyZWVkIHdpdGgKICAgICAgdGhlIGNvdXJ0LgogICAgLSBBYm91dCB0d28gdGltZXMgYXMgbWFueSBkZW1vY3JhdHMgdGhhbiByZXB1YmxpY2FucyBhZ3JlZWQgd2l0aAogICAgICB0aGUgY291cnQuCgoyLiBDb25zaWRlciB0aGUgc3RhY2tlZCBiYXIgY2hhcnQgcHJvZHVjZWQgYnkgdGhlIGZvbGxvd2luZyBjb2RlOgoKICAgIGBgYHtyLCBldmFsID0gRkFMU0UsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLXNob3cifQogICAgbGlicmFyeSh0aWR5dmVyc2UpCiAgICBtcGcyIDwtIG11dGF0ZShtcGcsCiAgICAgICAgICAgICAgICAgICBjbGFzcyA9IGZjdF9yZXYoZmN0X2luZnJlcShjbGFzcykpLAogICAgICAgICAgICAgICAgICAgY3lsID0gZmFjdG9yKGN5bCkpCiAgICBwIDwtIGdncGxvdChtcGcyLCBhZXMoeSA9IGNsYXNzLCBmaWxsID0gY3lsKSkgKwogICAgICAgIGdlb21fYmFyKCkKICAgIGBgYAoKICAgIFdoaWNoIG9mIHRoZXNlIG1vZGlmaWNhdGlvbnMgbWFrZXMgaXQgZWFzaWVzdCB0byBjb21wYXJlIHRoZSBjb3VudAogICAgb2YgNC1jeWxpbmRlciBtb2RlbHMgd2l0aGluIHRoZSBkaWZmZXJlbnQgY2xhc3Nlcz8KICAgIAogICAgYS4gYHAgJSslIG11dGF0ZShtcGcyLCBjeWwgPSBmYWN0b3IoY3lsLCBjKDQsIDUsIDYsIDgpKSlgCiAgICBiLiBgcCAlKyUgbXV0YXRlKG1wZzIsIGN5bCA9IGZhY3RvcihjeWwsIGMoOCwgNiwgNSwgNCkpKWAKICAgIGMuIGBwICUrJSBtdXRhdGUobXBnMiwgY3lsID0gZmFjdG9yKGN5bCwgYyg1LCA2LCA0LCA4KSkpYAogICAgZC4gYHAgJSslIG11dGF0ZShtcGcyLCBjeWwgPSBmYWN0b3IoY3lsLCBjKDQsIDYsIDgsIDUpKSlgCgozLiBUaGUgYmFyIGNoYXJ0IHByb2R1Y2VkIGJ5IHRoZSBmb2xsb3dpbmcgY29kZSBoYXMgYHhgIGF4aXMgbGFiZWxzCiAgIHRoYXQgY291bGQgYmUgaW1wcm92ZWQ6CgogICAgYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLXNob3cifQogICAgbGlicmFyeShnYXBtaW5kZXIpCiAgICBsaWJyYXJ5KGRwbHlyKQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgbGlicmFyeShzY2FsZXMpCiAgICBwIDwtIGZpbHRlcihnYXBtaW5kZXIsIHllYXIgPT0gMjAwNykgfD4KICAgICAgICBncm91cF9ieShjb250aW5lbnQpIHw+CiAgICAgICAgc3VtbWFyaXplKGF2Z0dkcFBlcmNhcCA9IG1lYW4oZ2RwUGVyY2FwKSkgfD4KICAgICAgICBnZ3Bsb3QoYWVzKHggPSBhdmdHZHBQZXJjYXAsIHkgPSBjb250aW5lbnQpKSArCiAgICAgICAgZ2VvbV9jb2woKSArCiAgICAgICAgICAgIGxhYnMoeCA9ICJBdmVyYWdlIEdEUCBQZXIgQ2FwaXRhIiwgeSA9IE5VTEwpICsKICAgICAgICAgICAgdGhlbWVfbWluaW1hbCgpICsgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTYpKQogICAgYGBgCgogICAgVGhlcmUgYXJlIGEgbnVtYmVyIG9mIGRpZmZlcmVudCBvcHRpb25zLiBXaGljaCBvZiB0aGUgZm9sbG93aW5nCiAgICBkb2VzICoqbm90KiogcHJvdmlkZSBpbXByb3ZlZCBgeGAgYXhpcyBsYWJlbHM/CgogICAgYS4gYHAgKyBzY2FsZV94X2NvbnRpbnVvdXMobGFiZWxzID0gbGFiZWxfY29tbWEoKSlgCiAgICBiLiBgcCArIHNjYWxlX3hfY29udGludW91cyhsYWJlbHMgPSBsYWJlbF9kb2xsYXIoKSlgCiAgICBjLiBgcCArIHNjYWxlX3hfY29udGludW91cyhsYWJlbHMgPSB1bml0X2Zvcm1hdChzY2FsZSA9IDEvMTAwMCwgdW5pdCA9ICJLIiwgcHJlZml4ID0gIiQiKSlgCiAgICBkLiBgcCArIHNjYWxlX3hfY29udGludW91cyhsYWJlbHMgPSBjKCIkMTAsMDAwIiwgIiQyMCwwMDAiLCAiJDMwLDAwMCIpKWAKCjQuIEEgc3RhY2tlZCBiYXIgY2hhcnQgaXMgYXBwcm9wcmlhdGUgaWYgdGhlIGNvbWJpbmVkIGJhciBoZWlnaHRzIG9mCiAgIHRoZSBzdGFja2VkIGJhcnMgaGF2ZSBhIHJlYXNvbmFibGUgaW50ZXJwcmV0YXRpb24uIENvbnNpZGVyIHRoZQogICBmb2xsb3dpbmcgdHdvIHBsb3RzOgoKCiAgICBgYGB7ciwgZmlnLmhlaWdodCA9IDQsIGZpZy53aWR0aCA9IDh9CiAgICBsaWJyYXJ5KGdhcG1pbmRlcikKICAgIGxpYnJhcnkoZHBseXIpCiAgICBsaWJyYXJ5KGdncGxvdDIpCiAgICBsaWJyYXJ5KHBhdGNod29yaykKICAgIHAxIDwtIGZpbHRlcihnYXBtaW5kZXIsIHllYXIgPj0gMjAwMCkgfD4KICAgICAgICBncm91cF9ieShjb250aW5lbnQsIHllYXIpIHw+CiAgICAgICAgc3VtbWFyaXplKGF2Z0xpZmVFeHAgPSBtZWFuKGxpZmVFeHApLCAuZ3JvdXBzID0gImRyb3AiKSB8PgogICAgICAgIGdncGxvdChhZXMoeCA9IGF2Z0xpZmVFeHAsIHkgPSBjb250aW5lbnQsIGZpbGwgPSBmYWN0b3IoeWVhcikpKSArCiAgICAgICAgZ2VvbV9jb2woKSArCiAgICAgICAgdGhlbWVfbWluaW1hbCgpICsKICAgICAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxMikpICsKICAgICAgICBzY2FsZV94X2NvbnRpbnVvdXMoZXhwYW5kID0gZXhwYW5zaW9uKG11bHQgPSBjKDAsIC4xKSkpICsKICAgICAgICBsYWJzKHggPSAiQXZlcmFnZSBMaWZlIEV4cGVjdGFuY3kiLAogICAgICAgICAgICAgeSA9IE5VTEwsCiAgICAgICAgICAgICBmaWxsID0gIlllYXIiLAogICAgICAgICAgICAgdGl0bGUgPSAiQXZlcmFnZSBMaWZlIEV4cGVjdGFuY3lcbmJ5IENvbnRpbmVudCBmb3IgVHdvIFllYXJzIiwKICAgICAgICAgICAgIHRhZyA9ICJQMToiKQogICAgcDIgPC0gY291bnQobXBnLCBjbGFzcywgY3lsKSB8PgogICAgICAgIGdncGxvdChhZXMoeCA9IG4sIHkgPSBjbGFzcywgZmlsbCA9IGZhY3RvcihjeWwpKSkgKwogICAgICAgIGdlb21fY29sKCkgKwogICAgICAgIHRoZW1lX21pbmltYWwoKSArCiAgICAgICAgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTIpKSArCiAgICAgICAgc2NhbGVfeF9jb250aW51b3VzKGV4cGFuZCA9IGV4cGFuc2lvbihtdWx0ID0gYygwLCAuMSkpKSArCiAgICAgICAgbGFicyh4ID0gIk51bWJlciBvZiBNb2RlbHMiLAogICAgICAgICAgICAgeSA9IE5VTEwsCiAgICAgICAgICAgICBmaWxsID0gIkN5bGluZGVycyIsCiAgICAgICAgICAgICB0aXRsZSA9ICJOdW1iZXIgb2YgQ2FyIE1vZGVsc1xuYnkgQ2xhc3MgYW5kIEN5bGluZGVyIENvdW50IiwKICAgICAgICAgICAgIHRhZyA9ICJQMjoiKQogICAgcDEgKyBwMgogICAgYGBgCgogICAgV2hpY2ggb2YgdGhlIGZvbGxvd2luZyBzdGF0ZW1lbnRzIGlzIHRydWU6CgogICAgYS4gUDEgaXMgYW4gYXBwcm9wcmlhdGUgdXNlIG9mIGEgc3RhY2tlZCBiYXIgY2hhcnQgYnV0IFAyIGlzIG5vdC4KICAgIGIuIFAyIGlzIGFuIGFwcHJvcHJpYXRlIHVzZSBvZiBhIHN0YWNrZWQgYmFyIGNoYXJ0IGJ1dCBQMSBpcyBub3QuCiAgICBjLiBOZWl0aGVyIFAxIG5vciBQMiBpcyBhbiBhcHByb3ByaWF0ZSB1c2Ugb2YgYSBzdGFja2VkIGJhciBjaGFydC4KICAgIGQuIEJvdGggUDEgYW5kIFAyIGFyZSBhcHByb3ByaWF0ZSB1c2VzIG9mIGEgc3RhY2tlZCBiYXIgY2hhcnQuCg==


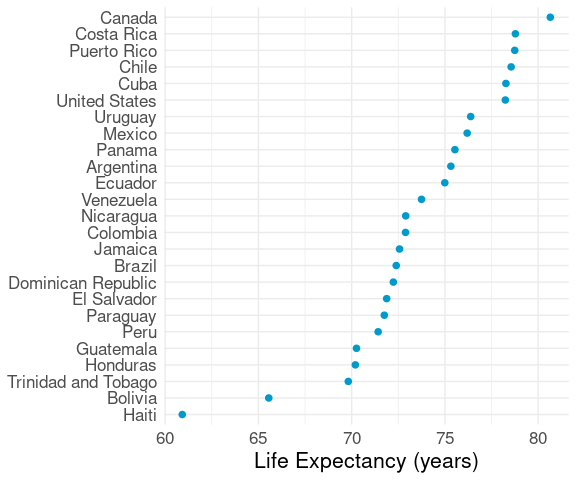
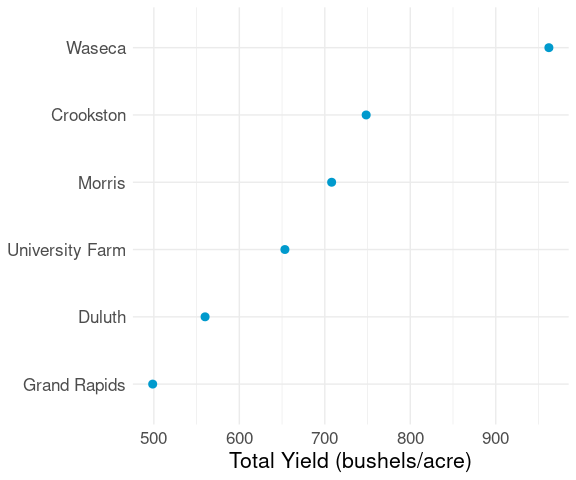
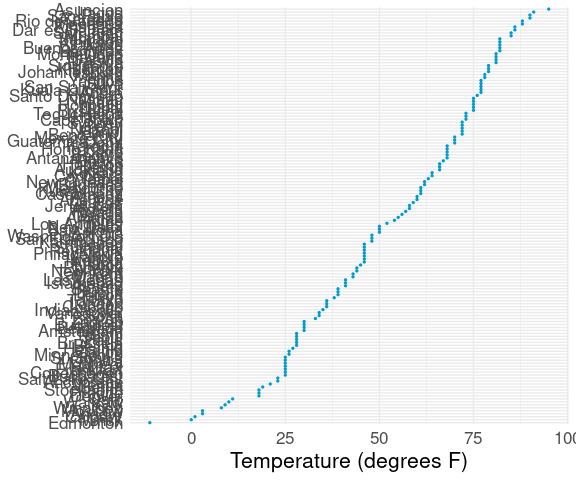
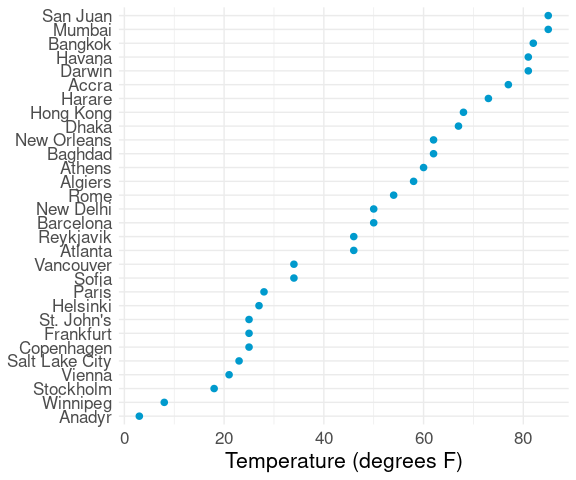

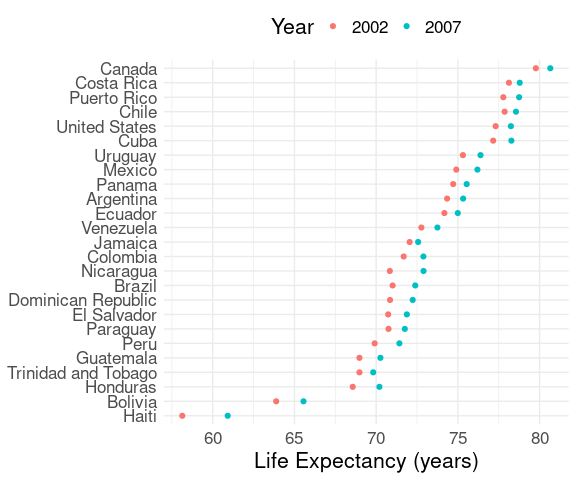
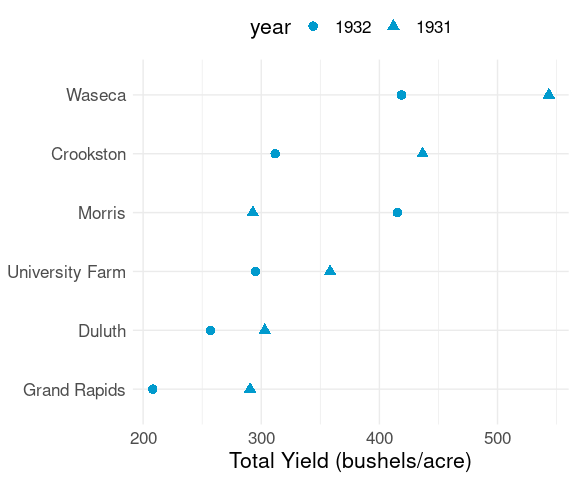

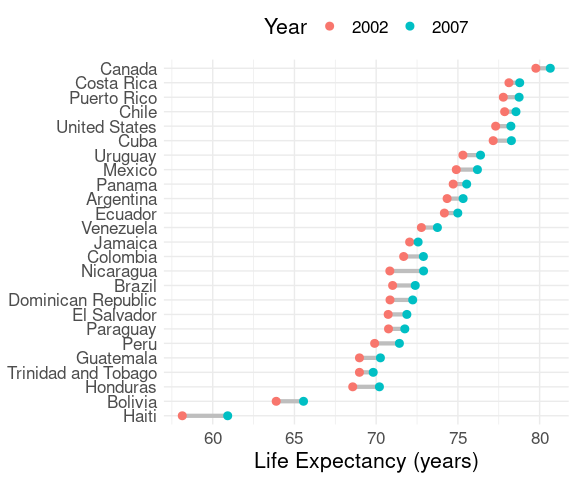
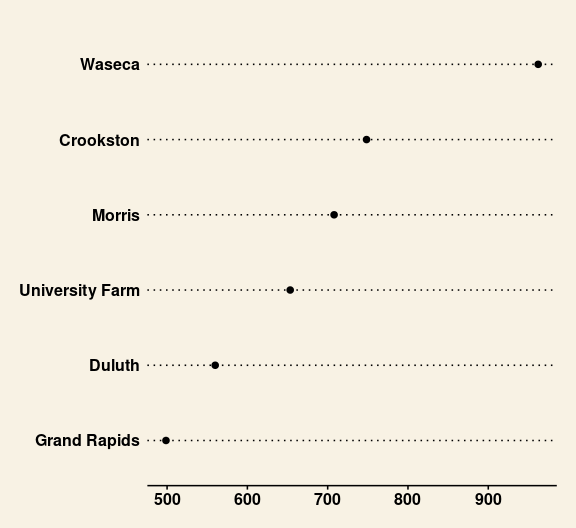
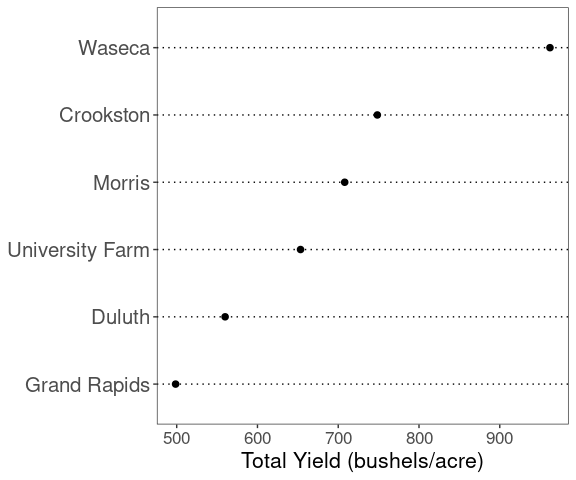
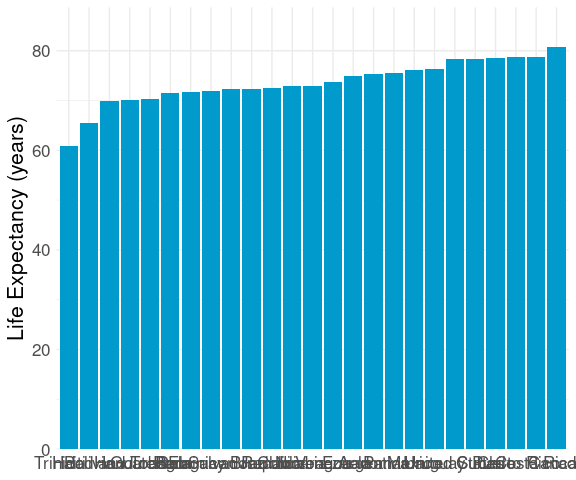

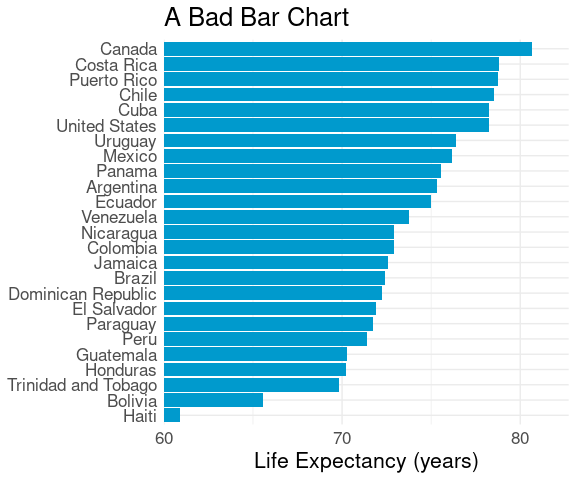
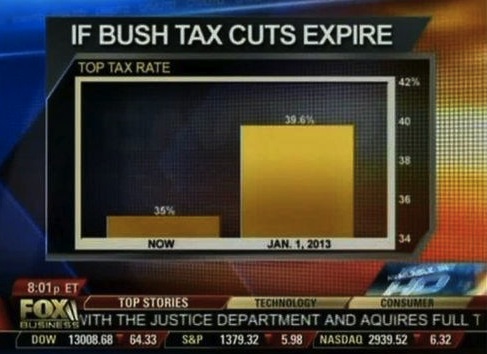
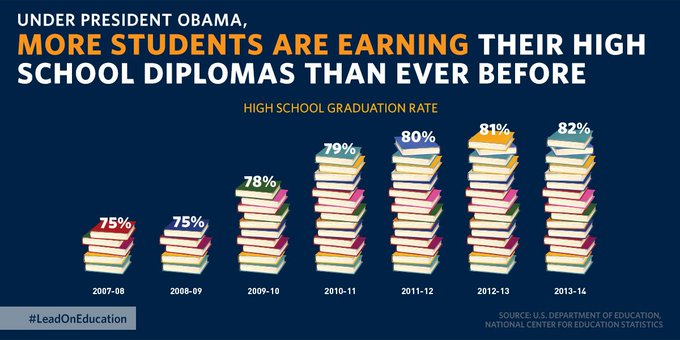
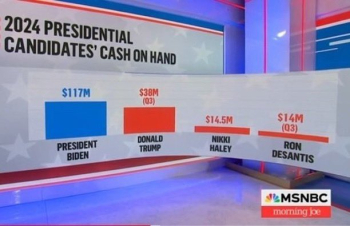
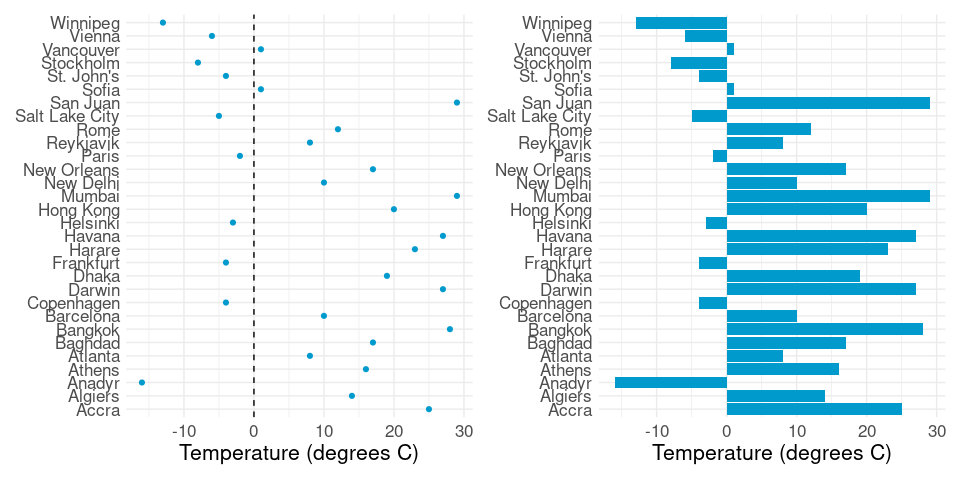
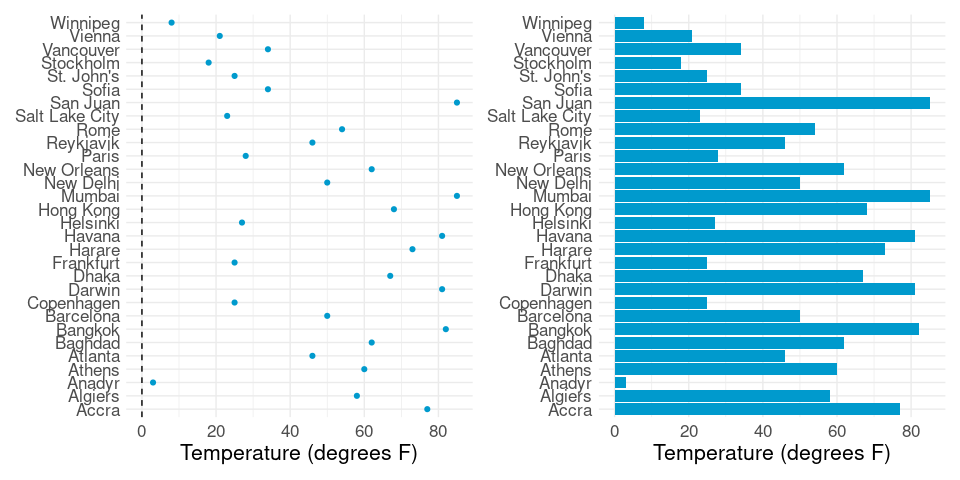
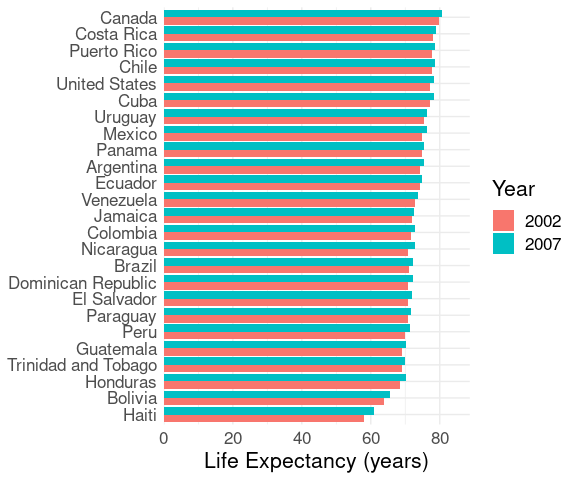
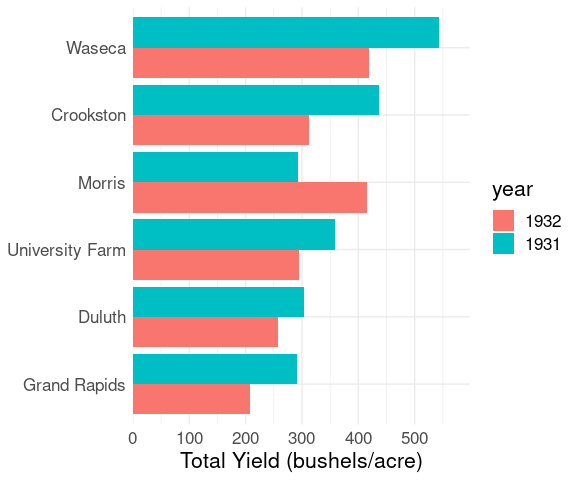
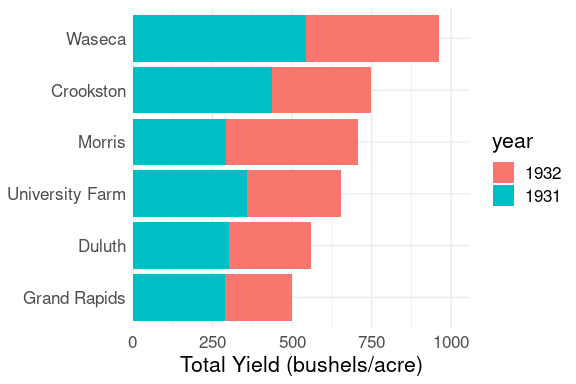
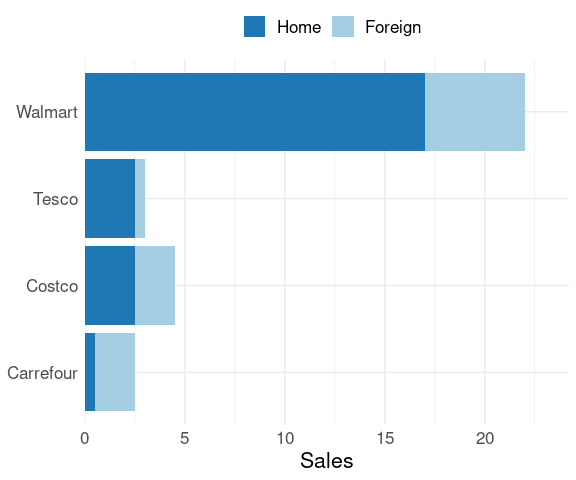
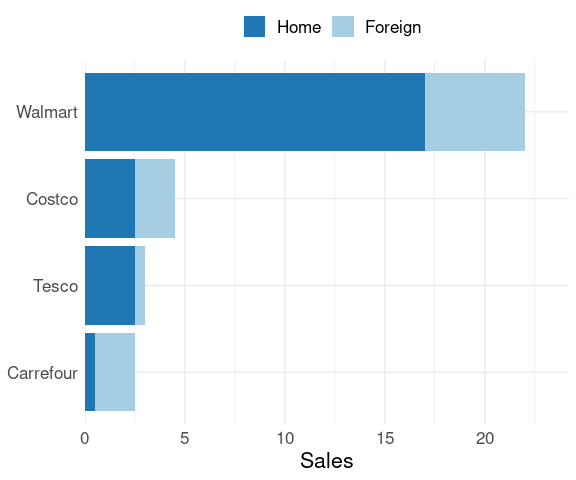
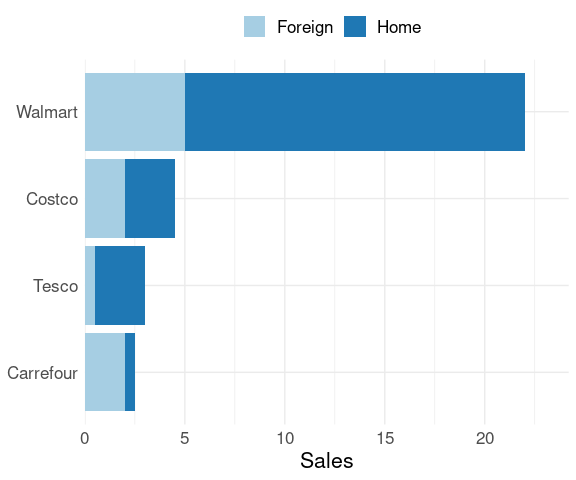
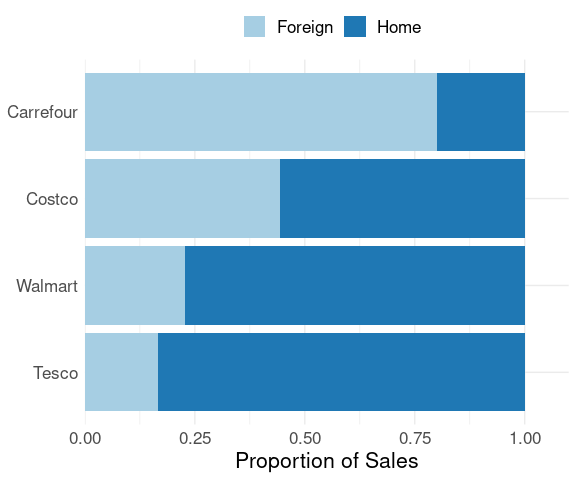 This no longer shows the differing total sales.
This no longer shows the differing total sales.