Color is very effective when used well.
But using color well is not easy.
Some of the issues:
Perception depends on context.
Simple color assignments may not separate equally well.
Effectiveness may vary with the medium (screen, projector, print).
Some people do not perceive the full spectrum of colors.
Grey scale printing.
Some colors have cultural significance.
Cultural significance may vary among cultures and with time.
An internet “controversy” in 2015: The Dress (and a follow-up article )
Color Spaces
RGB and HSV Color Spaces
Computer monitors and projectors work in terms of red, green, and blue light.
Amounts of red green and blue (and alpha level) are stored as integers in the range between 0 and 255 (8-bit bytes).
cols <- c("red", "green", "blue", "yellow", "cyan", "magenta")
rgbcols <- col2rgb(cols); colnames(rgbcols) <- cols
rgbcols
## red green blue yellow cyan magenta
## red 255 0 0 255 0 255
## green 0 255 0 255 255 0
## blue 0 0 255 0 255 255Colors are often encoded in hexadecimal form (base 16).
rgb(1, 0, 0) ## pure red
## [1] "#FF0000"
rgb(0, 0, 1) ## pure blue
## [1] "#0000FF"rgb(255, 0, 0, maxColorValue = 255)
## [1] "#FF0000"
rgb(0, 0, 255, maxColorValue = 255)
## [1] "#0000FF"Hue, saturation, value (HSV) is a simple transformation of RGB.
rgb2hsv(rgbcols)
## red green blue yellow cyan magenta
## h 0 0.3333333 0.6666667 0.1666667 0.5 0.8333333
## s 1 1.0000000 1.0000000 1.0000000 1.0 1.0000000
## v 1 1.0000000 1.0000000 1.0000000 1.0 1.0000000HSV is a little more convenient since it allows the hue to be controlled separately.
A simple color picker: https://www.google.com/search?q=color+picker
But saturation and value attributes are not particularly useful for specifying colors that work well perceptually.
A color wheel of fully saturated colors:
wheel <- function(col, radius = 1, ...)
pie(rep(1, length(col)),
col = col, radius = radius, ...)
wheel(rainbow(6))
Removing saturation:
library(colorspace)
wheel(desaturate(rainbow(6)))
Fully saturated yellow is brighter than red, which is brighter than blue.
HCL Color Space
The rainbow palette of the color wheel is often a default in visualization systems.
A blog post illustrates why this is a bad idea.
The rainbow hues are evenly spaced in the color spectrum, but chroma and luminance are not.
Luminance in particular is not monotone across the palette.
rgb2hcl <- function(col) {
## ignores alpha
col <- RGB(t(col[1 : 3, ]) / 255)
col <- as(col, "polarLUV")
col <- t(col@coords[, 3 : 1, drop = FALSE])
rownames(col) <- tolower(rownames(col))
col
}
col2hcl <- function(col) rgb2hcl(col2rgb(col))
pal <- function(col, border = "light gray", ...) {
n <- length(col)
plot(0, 0, type = "n", xlim = c(0, 1), ylim = c(0, 1),
axes = FALSE, xlab = "", ylab = "", ...)
rect((0 : (n - 1)) / n, 0, (1 : n) / n, 1, col = col, border = border)
}
par(mfrow = c(1, 2))
pal(rainbow(6), main = "Saturated Rainbow")
pal(desaturate(rainbow(6)), main = "Desaturated")
specplot(rainbow(6), ldw = 4)
The hue, chroma, luminance (HCL ) space allows separate control of:
Hue , the color.
Chroma , the amount of the color.
Luminance , or perceived brightness.
HCL makes it easier to create perceptually uniform color palettes.
A palette with constant chroma, evenly spaced hues and evenly spaced luminance values:
rain6 <- hcl(seq(0, 360 * 5 / 6, len = 6), 50, seq(60, 80, len = 6))
par(mfrow = c(1, 2))
pal(rain6, main = "Uniform Rainbow")
pal(desaturate(rain6), main = "Desaturated")
specplot(rain6, lwd = 4)
For a fully saturated red, varying only chroma to reduce the amount of color:
red_hcl <- list(h = 12.17395, c = 179.04076, l = 53.24059)
specplot(hcl(red_hcl$h, red_hcl$c * seq(0, 1, len = 10), red_hcl$l), lwd = 4)
For a given hue, not all combinations of chroma and luminance are possible.
In particular, for low luminance values the available chroma range is limited.
The ggplot book
Hue is mapped to angle.
Chroma is mapped to radius.
Luminance is mapped to facets.
The origins with zero chroma are shades of grey.
HCL color picker.
HCL is a transformation of the CIEluv color space designed for perceptual uniformity.
The definition of the luminance takes into account the light sensitivity of a standard human observer at various wave lengths.
Light sensitivity for different wave lengths in daylight conditions (photopic vision) and under dark adapted conditions (scotopic vision):
Munsell Color Space
Another color space, similar to HCL, is the Munsell system developed in the early 1900s.
This system uses a Hue, Value, Chroma encoding.
The munsell packageggplot.
Munsell specifications are of the form "H V/C", such as 5R 5/10.
Possible hues are
library(munsell, exclude = "desaturate")
mnsl_hues()
## [1] "2.5R" "5R" "7.5R" "10R" "2.5YR" "5YR" "7.5YR" "10YR" "2.5Y"
## [10] "5Y" "7.5Y" "10Y" "2.5GY" "5GY" "7.5GY" "10GY" "2.5G" "5G"
## [19] "7.5G" "10G" "2.5BG" "5BG" "7.5BG" "10BG" "2.5B" "5B" "7.5B"
## [28] "10B" "2.5PB" "5PB" "7.5PB" "10PB" "2.5P" "5P" "7.5P" "10P"
## [37] "2.5RP" "5RP" "7.5RP" "10RP"V should be an integer between 0 and 10.
C should be an even integer less than 24, but not all combinations are possible.
Adjusting colors in the value, chroma, and hue dimensions:
my_blue <- "5PB 5/8"
plot_mnsl(c(
lighter(my_blue, 2), my_blue, darker(my_blue, 2),
munsell::desaturate(my_blue, 2), my_blue, saturate(my_blue, 2),
rygbp(my_blue, 2), my_blue, pbgyr(my_blue, 2)))Creating scales:
plot_mnsl(sapply(0 : 6, darker, col = "5PB 7/4")) + facet_wrap(~ num, nrow = 1)
Examining available colors:
hue_slice("5R")
value_slice(5)
Complementary colors:
complement_slice("5R")
Opponent Process Theory
The Opponent Process Model of vision says that the brain divides the visual signal among three opposing contrast pairs:
black and white;
red and green;
yellow and blue.
The black/white pair corresponds to luminance in HCL
Hue and chroma in HCL span the two chromatic axes.
The luminance axis has higher resolution than the two chromatic axes.
The major form of color vision deficiency reflects an inability to distinguish differences along the red/green axis.
Impairment along the yellow/blue axis does occur as well but is much rarer.
Contrast and Comparisons
Vision reacts to differences, not absolutes.
Small differences in shading or hue can be recognized when objects are contiguous but be much harder to see when they are separated.
Simultaneous brightness contrast : a grey patch on a dark background looks lighter than the same grey patch on a light background.
plot(0, 0, type = "n", xlim = c(0, 1), ylim = c(0, 1),
axes = FALSE, xlab = "", ylab = "")
rect(0, 0, 0.5, 1, col = "lightgrey", border = NA)
rect(0.5, 0, 1, 1, col = "darkgrey", border = NA)
rect(0.2, 0.3, 0.3, 0.7, col = "grey", border = NA)
rect(0.7, 0.3, 0.8, 0.7, col = "grey", border = NA)
An example we saw earlier:
Some more are available here , including:
Using luminance or grey scale alone does not work well for encoding categorical variables against a key.
Grey scale can be effective for showing continuous transitions in pseudo-color images.
filled.contour(volcano, color.palette = grey.colors)
Grey scale is less effective for segmented maps, or choropleth maps; only a few levels can be accurately decoded.
Interactions with Size, Background and Proximity
For small items more contrast and more saturated colors are needed:
x <- runif(6, 0.1, 0.9)
y <- runif(6, 0.1, 0.9)
cols <- c("red", "green", "blue", "yellow", "cyan", "magenta")
f <- function(size = 1, black = FALSE) {
plot(x, y, type = "n", xlim = c(0, 1), ylim = c(0, 1))
if (black) rect(0, 0, 1, 1, col = "black")
text(x, y, cols, col = cols, cex = size)
}
opar <- par(mfrow = c(2, 2))
f(1)
f(4)
f(1, TRUE)
f(4, TRUE)
par(opar)Variations in luminance are particularly helpful for seeing fine structure, such as small text or small symbols:
plot(0, type = "n", xlim = c(0, 1), ylim = c(0, 1),
axes = FALSE, xlab = "", ylab = "")
rect(0, 0, 1, 1, col = hcl(0)) ## defaults: c = 35, l = 85
qbf <- "The quick brown fox jumps ..."
text(0.5, 0.3, label = qbf, col = hcl(180)) ## hue
text(0.5, 0.5, label = qbf, col = hcl(0, c = 70)) ## chroma
text(0.5, 0.7, label = qbf, col = hcl(0, l = 50)) ## luminance
Chrominance (hue and chroma) differences alone are not sufficient for small items.
Ware recommends a luminance contrast of at least 3:1 for small text; 10:1 is preferable.
Small areas also need variation in more than hue:
Contrasting borders can help for larger areas with similar luminance:
Color Specification in R
A large number of named colors are available (currently 657).
Some examples:
col2rgb("red")
## [,1]
## red 255
## green 0
## blue 0
col2rgb("forestgreen")
## [,1]
## red 34
## green 139
## blue 34
col2rgb("deepskyblue")
## [,1]
## red 0
## green 191
## blue 255
col2rgb("firebrick")
## [,1]
## red 178
## green 34
## blue 34These will show some details:
colors()
demo(colors)The available named colors follow a widely used standard .
These colors include the 140 web colors
Individual colors can also be specified using rgb() or hcl() or as hexadecimal specifications.
library(colorspace)
hex2RGB("#FF0000")
## R G B
## [1,] 1 0 0Using color spaces:
rgb(1, 0, 0)
## [1] "#FF0000"
rgb(255, 0, 0, max = 255)
## [1] "#FF0000"
rgb2hsv(col2rgb("red"))
## [,1]
## h 0
## s 1
## v 1Converting to HCL:
rgb2hcl <- function(col) {
## ignores alpha
col <- RGB(t(col[1 : 3, ]) / 255)
col <- as(col, "polarLUV")
col <- t(col@coords[, 3 : 1, drop = FALSE])
rownames(col) <- tolower(rownames(col))
col
}
col2hcl <- function(col) rgb2hcl(col2rgb(col))
col2hcl("red")
## [,1]
## h 12.17395
## c 179.04076
## l 53.24059
col2hcl("green")
## [,1]
## h 127.7235
## c 135.7811
## l 87.7351
col2hcl("blue")
## [,1]
## h 265.87278
## c 130.67593
## l 32.29567
col2hcl("yellow")
## [,1]
## h 85.87351
## c 107.06462
## l 97.13951
col2hcl("cyan")
## [,1]
## h 192.16714
## c 72.09794
## l 91.11330
col2hcl("magenta")
## [,1]
## h 307.72618
## c 137.40166
## l 60.32351
hcl(12.17, 179.04, 53.24)
## [1] "#FF0000"Color pickers can help:
When a set of colors is needed to encode variable values it is usually best to use a suitable palette .
Color Palettes
Color palettes are collections of colors that work well together.
It is useful to distinguish three kinds of palettes:
Tools for selecting palettes include:
A blog post with some further options.
Some current US government work on color palettes; more extensive notes and code .
R color palette functions:
rainbow()heat.colors()terrain.colors()topo.colors()cm.colors()grey.colors()gray.colors()
These all take the number of colors as an argument, as well as some additional optional arguments.
The hcl.color() function provides access to the palettes defined in the colorspace package.
colorRampPalette() can be used to create a palette function that interpolates between a set of colors using
rwb <- colorRampPalette(
c("red", "white", "blue"))
rwb(5)
## [1] "#FF0000" "#FF7F7F" "#FFFFFF" "#7F7FFF" "#0000FF"filled.contour(volcano,
color.palette = rwb,
asp = 1)
With more perceptually comparable extremes (from the Blue-Red palette of HCL Wizard):
rwb1 <- colorRampPalette(
c("#8E063B", "white", "#023FA5"))
filled.contour(volcano,
color.palette = rwb1,
asp = 1)
An alternative uses the muted function from package scales:
rwb2 <- colorRampPalette(
c(scales::muted("red"),
"white",
scales::muted("blue")))
filled.contour(volcano,
color.palette = rwb2,
asp = 1)
Most base and lattice functions allow a vector of colors to be specified.
Some, like filled.contour() and levelplot() allow a palette function to be provided.
ggplot provides a framework for specifying palette functions to use with scale_color_xyz() and scale_fill_xyz() functions.
Packages like colorspace and viridis provide additional scale_color_xyz() and scale_fill_xyz() functions.
RColorBrewer Palettes
The available palettes:
library(RColorBrewer)
display.brewer.all()Palettes in the first group are sequential .
The second group are qualitative .
The third group are diverging .
The "Blues" palette:
display.brewer.pal(9, "Blues")
As RGB values:
brewer.pal(9, "Blues")
## [1] "#F7FBFF" "#DEEBF7" "#C6DBEF" "#9ECAE1" "#6BAED6" "#4292C6" "#2171B5"
## [8] "#08519C" "#08306B"The palettes are limited to a maximum number of levels.
To obtain more levels you can interpolate.
brewer.pal(10, "Blues")
## Warning in brewer.pal(10, "Blues"): n too large, allowed maximum for palette Blues is 9
## Returning the palette you asked for with that many colors
## [1] "#F7FBFF" "#DEEBF7" "#C6DBEF" "#9ECAE1" "#6BAED6" "#4292C6" "#2171B5"
## [8] "#08519C" "#08306B"
pbrbl <- colorRampPalette(brewer.pal(9, "Blues"), interpolate = "spline")
pbrbl
## function (n)
## {
## x <- ramp(seq.int(0, 1, length.out = n))
## if (ncol(x) == 4L)
## rgb(x[, 1L], x[, 2L], x[, 3L], x[, 4L], maxColorValue = 255)
## else rgb(x[, 1L], x[, 2L], x[, 3L], maxColorValue = 255)
## }
## <bytecode: 0x55b7942c4cb8>
## <environment: 0x55b78c99f8d0>
pbrbl(10)
## [1] "#F7FBFF" "#E0ECF7" "#CCDEF1" "#ADD0E5" "#81BBDA" "#57A1CF" "#3687C0"
## [8] "#1A69B0" "#064D98" "#08306B"
Colorspace Palettes
The colorspace package provides a wide range of pre-defined palettes:
library(colorspace)
hcl_palettes(plot = TRUE)
A particular number of colors from one of these palettes can be obtained with
qualitative_hcl(4, palette = "Dark 3")
## [1] "#E16A86" "#909800" "#00AD9A" "#9183E6"The functions sequential_hcl() and diverging_hcl() are analogous.
For use with ggplot2 the package provides scale functions like scale_fill_discrete_qualitative() and scale_color_continuous_sequential().
A package vignette provides more details and background.
Viridis Palettes
These are provided in package viridisLite.
Palette functions are viridis(), mako(), etc..
They are also available via the hcl.colors() function.
For use in ggplot they can be specified in the viridis color scale functions.
Palettes in R Graphics
ggplot uses scale_color_xyz() or scale_fill_xyz().
For discrete scales the choices for xyz include
hue varies the hue (default for unordered factors);grey uses grey scale;brewer uses ColorBrewer palettes;manual allows explicit specification.viridis_d for an alternative palette family (default for orderer factors).
For continuous scales the choices for xyz include
gradient interpolates between two colors, low and high;gradient2 interpolates between three colors, low, medium, high;gradientn interpolates between a vector of colors;distiller for ColorBrewer palettes.viridis_c for an alternative palette family.
Others are available in packages such as colorspace.
The default qualitative and sequential discrete palettes:
library(gapminder)
gap_2007 <- filter(gapminder, year == 2007) |> slice_max(pop, n = 20)
p <- mutate(gap_2007, country = reorder(country, pop)) |>
ggplot(aes(x = gdpPercap, y = lifeExp, fill = continent)) +
scale_size_area(max_size = 10) +
scale_x_log10() +
geom_point(size = 4, shape = 21) +
guides(fill = guide_legend(override.aes = list(size = 4)))
p1 <- p + ggtitle("Hue")
p2 <- p + scale_fill_viridis_d() + ggtitle("Viridis")
library(patchwork)
p1 + p2
Discrete examples for brewer, colorspace and manual:
p1 <- p + scale_fill_brewer(palette = "Set1") +
ggtitle("Brewer Set1")
p2 <- p + scale_fill_brewer(palette = "Set2") +
ggtitle("Brewer Set2")
p3 <- p + scale_fill_discrete_qualitative("Dark 3") +
ggtitle("Colorspace Dark 3")
p4 <- p + scale_fill_manual(values = c(Africa = "red", Asia = "blue",
Americas = "green", Europe = "grey")) +
ggtitle("Manual")
(p1 + p2) / (p3 + p4)
The default for continuous scales is gradient from a dark blue to a light blue:
V <- data.frame(x = rep(seq_len(nrow(volcano)), ncol(volcano)),
y = rep(seq_len(ncol(volcano)), each = nrow(volcano)),
z = as.vector(volcano))
p <- ggplot(V, aes(x, y, fill = z)) + geom_raster() + coord_fixed()
p
Some alternatives:
p1 <- p + scale_fill_gradient2(
low = "red", mid = "white", high = "blue",
midpoint = median(volcano)) +
ggtitle("Red-White-Blue Gradient")
p2 <- p + scale_fill_viridis_c() +
ggtitle("Viridis")
p3 <- p + scale_fill_gradientn(
colors = terrain.colors(8)) +
ggtitle("Terrain")
vbins <- seq(80, by = 20, length.out = 7)
nc <- length(vbins) - 1
p4 <- ggplot(mutate(V, z = fct_rev(cut(z, vbins))),
aes(x, y, fill = z)) +
geom_raster() +
scale_fill_manual(values = rev(terrain.colors(nc))) +
ggtitle("Discretized Terrain")
(p1 + p2) / (p3 + p4)Discretizing a continuous range to a modest number of levels can make decoding values from a legend easier.
Reduced Color Vision
Color vision deficiency affects about 10% of males, a smaller percentage of females.
The most common form is reduced ability to distinguish red and green.
Some web sites provide tools to simulate how a visualization would look to a color vision deficient viewer.
The R packages dichromat, colorspace, and colorblindr provide tools for simulating how colors would look to a color vision deficient viewer for three major types of color vision deficiency:
deuteranomaly (green cone cells defective);
protanomaly (red cone cells defective);
tritanomaly (blue cone cells defective).
An article explaining the color vision impairment simulation is available here
Using some tools from packages colorspace and colorblinder we can simulate what a plot would look like in grey scale and to someone with some of the major types of color impairment.
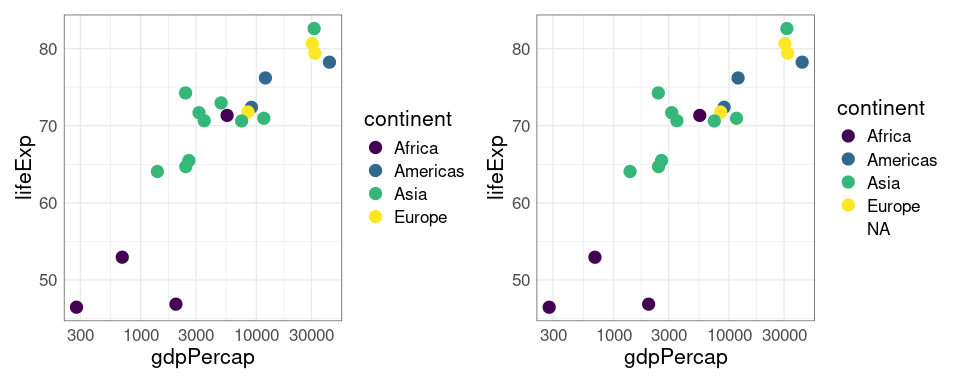
A plot with the default discrete color palette:
p <- ggplot(gap_2007, aes(gdpPercap, lifeExp, color = continent)) +
geom_point(size = 4) +
scale_x_log10() +
guides(color = guide_legend(override.aes = list(size = 4)))
p
library(colorblindr)
library(colorspace)
library(grid)
color_check <- function(p) {
p1 <- edit_colors(p + ggtitle("Desaturated"), desaturate)
p2 <- edit_colors(p + ggtitle("deutan"), deutan)
p3 <- edit_colors(p + ggtitle("protan"), protan)
p4 <- edit_colors(p + ggtitle("tritan"), tritan)
gridExtra::grid.arrange(p1, p2, p3, p4, nrow = 2)
}
color_check(p)
For the Viridis palette:
pv <- p + scale_color_viridis_d()
pv
color_check(pv)
The swatchplot() function in the colorspace package can be used with the cvd = TRUE argument to simulate how specific palettes work for different color vision deficiencies:
colorspace::swatchplot(rainbow(6), cvd = TRUE)
colorspace::swatchplot(hcl.colors(6), cvd = TRUE)
Two Issues to Watch Out For
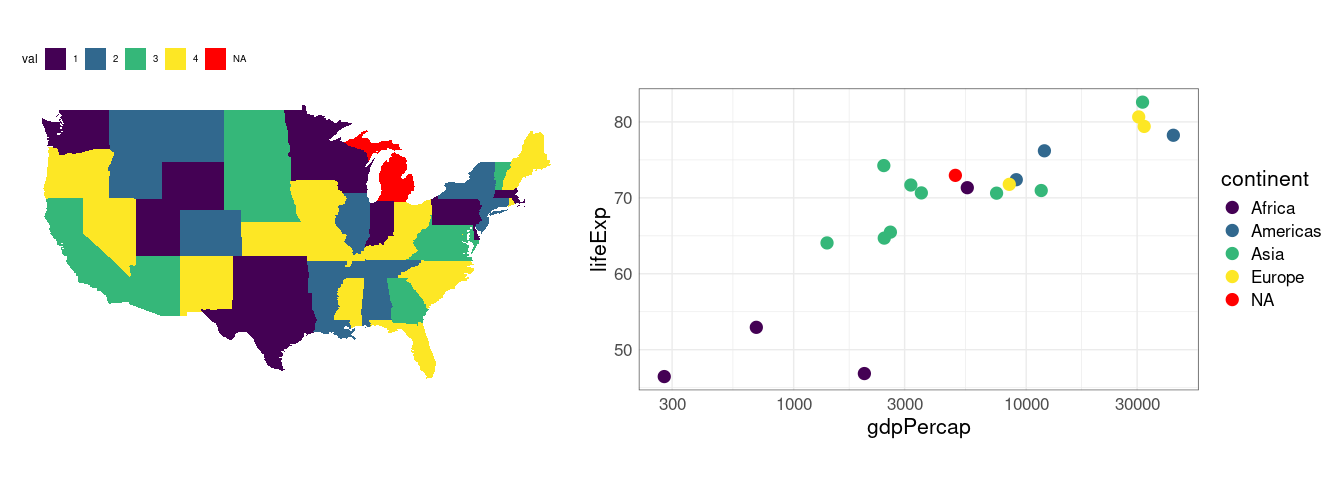
Missing Values
It is common for default settings to not assign a color for missing values.
In a choropleth map with (made-up) data where one state’s value is missing this might not be noticed.
m <- map_data("state")
d <- data.frame(region = unique(m$region),
val = ordered(sample(1 : 4, 49, replace = TRUE)))
m <- left_join(m, d, "region")
pm <- ggplot(m) +
geom_polygon(aes(long, lat, group = group, fill = val)) +
coord_map() +
ggthemes::theme_map()
dnm <- mutate(m, val = replace(val, region == "michigan", NA))
pm %+% dnm
Or is from Michigan.
In a scatterplot there are even fewer cues:
gnc <- mutate(gap_2007, continent = replace(continent, country == "China", NA))
pv +
pv %+% gnc
## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_point()`).
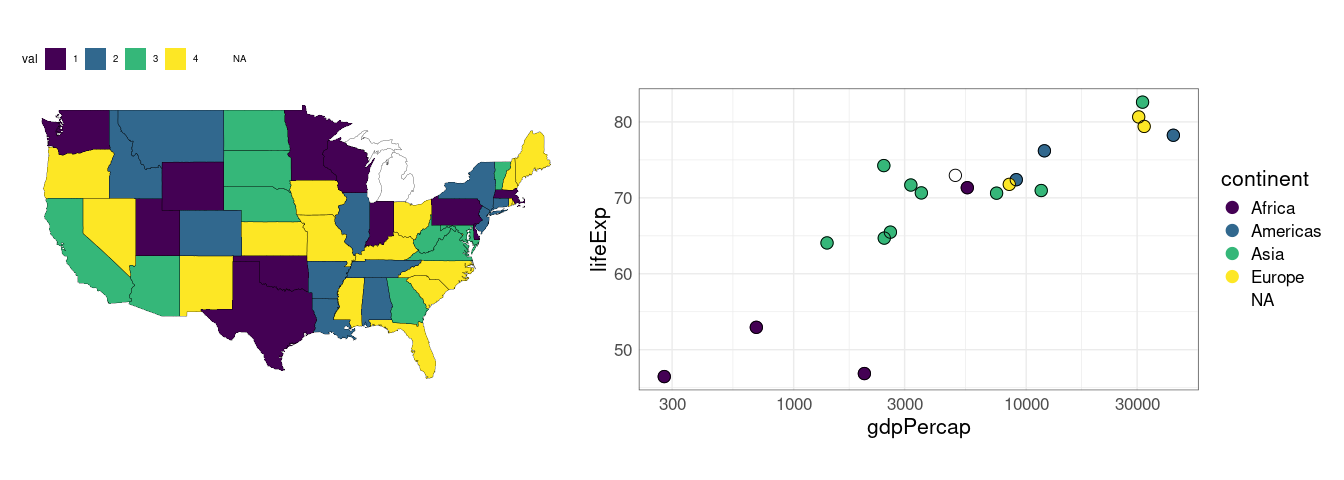
Specifying na.value = "red", or some other color, will make sure NA values are visible:
(pm %+% dnm +
scale_fill_viridis_d(na.value = "red") + theme(legend.position = "top")) +
(pv %+% gnc + scale_color_viridis_d(na.value = "red"))
## Scale for colour is already present.
## Adding another scale for colour, which will replace the existing scale.
Using outlines can also help:
p1 <- pm %+% dnm +
geom_polygon(aes(long, lat, group = group),
fill = NA, color = "black", linewidth = 0.1) +
theme(legend.position = "top")
p2 <- pv %+% gnc +
geom_point(shape = 21, fill = NA, color = "black", size = 4)
p1 + p2
## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_point()`).
A final plot might handle missing values differently, but for initial explorations it is a good idea to make sure they are clearly visible.
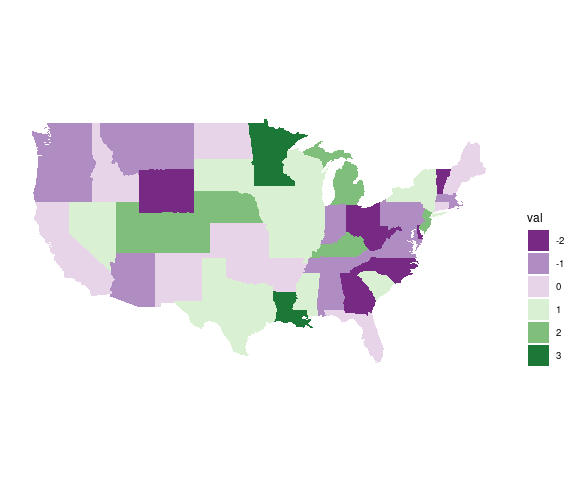
Aligning Diverging Palettes
Diverging palettes are very useful for showing deviations above or below a baseline.
par(mfrow = c(1, 2))
RColorBrewer::display.brewer.pal(7, "PRGn")
RColorBrewer::display.brewer.pal(6, "PRGn")
For a diverging palette to work properly, the palette base line needs to be aligned with the data baseline.
How to do this will depend on the palette, but you do need to keep this in mind when using a diverging palette.
Just using scale_fill_brewer is not enough when the value range is not symmetric around the baseline:
m <- map_data("state")
d <- data.frame(region = unique(m$region),
val = ordered(sample((1 : 6) - 3, 49, replace = TRUE)))
m <- left_join(m, d, "region")
p <- ggplot(m) +
geom_polygon(aes(long, lat, group = group, fill = val)) +
coord_map() +
ggthemes::theme_map() +
theme(legend.position = "right")
p + scale_fill_brewer(palette = "PRGn")
Setting the scale limits explicitly forces a 7-category symmetric scale that aligns the zero value with the middle color:
lims <- as.character(-3 : 3)
p + scale_fill_brewer(palette = "PRGn",
limits = lims)
This shows a category in the legend for -3 that does not appear in the map.
This is often what you want.
But if you want to drop the -3 category, one option is to use a manual scale:
vals <- RColorBrewer::brewer.pal(7, "PRGn")
names(vals) <- lims
p + scale_fill_manual(values = vals[-1])
Bivariate Palettes
It is possible to encode two variables in a palette.
Some sample palettes:
Bivariate palettes are sometimes used in bivariate choropleth maps .
Some recommendations from Cynthia Brewer are available here .
A discussion of a recent example.
Unless one variable is binary, and the palette is very well chosen, it is hard to decode a visualization using a binary palette without constantly referring to the key.
Culture, Tradition, and Conventions
Colors can have different meanings in different cultures and at different times.
Conventions can also give colors particular meanings:
red/green in traffic lights;
red/green colors in microarray heatmaps;
red states and blue states;
pink for breast cancer;
pink for girls, blue for boys;
black for mourning.
Traffic Lights
Traffic lights use red/green, even though this is a major axis of color vision deficiency.
The convention comes from railroads.
The red used generally contains some orange and the green contains blue to help with red/green color vision deficiency.
Position provides an alternate encoding. Orientations do vary.
Microarray Heatmaps
Microarrays are used for the analysis of gene-level changes and differences in bio-medical research.Dyes are used that result in genes with a high response appearing red and genes with a low response appearing green.
In keeping with this physical characteristic of microarrays, a common visualization of the data is as a red/green heat map.
Red States and Blue States
It is now standard in the US to refer to Republican-leaning states as red states and Democrat-leaning states as blue states.
This is a fairly recent convention, dating back to the 2000 presidential election.
Prior to 1980 it was somewhat more traditional to use red for more left-leaning Democrats.
A map of the 1960 election results uses these more traditional colors.
In 1996 the New York Times used blue for Democrat, red for Republican, but the Washington Post used the opposite color scheme.
The long, drawn out process of the 2000 election may have contributed to fixing the color schema at the current convention.
Notes
Points need more saturation, luminance than areas.
False color images may benefit from discretizing.
Bivariate encodings (e.g. x = hue, y = luminance) are possible but tricky and not often a good idea. Best if at least one is binary.
Providing a second encoding, e.g. shape, position can help for color vision deficient viewers and photocopying.
In area plots and maps it is important to distinguish between base line values and missing values.
If observed values only cover part of a possible range, it is sometimes appropriate to use a color coding that applies to the entire possible range.
For diverging palettes, some care may be needed to make sure the neutral color and the neutral value are properly aligned.
Using a well-designed palette is usually better than creating your own.
Choosing a palette can consider many factors, including appearance and branding.
A UI Diverging Palette?
UI color guidelines are spelled out in the brand manual .
UIgold <- rgb(255, 205, 0, maxColorValue=255)
pdUI <- colorRampPalette(c("black", "white", UIgold))
colorspace::swatchplot(pdUI(5))
colorspace::swatchplot(pdUI(5), cvd = TRUE)
References
Few, Stephen. “Practical rules for using color in charts.” Visual Business Intelligence Newsletter 11 (2008): 25. (PDF )
Harrower, M. A. and Brewer, C. M. (2003). ColorBrewer.org: An online tool for selecting color schemes for maps. The Cartographic Journal , 40, 27–37. ColorBrewer web site . The RColopBrewer package provides an R interface.
Ihaka, R. (2003). Colour for presentation graphics, in K. Hornik, F. Leisch, and A. Zeileis (eds.), Proceedings of the 3rd International Workshop on Distributed Statistical Computing PDF . See also the colorspace package and vignette .
Lumley, T. (2006). Color coding and color blindness in statistical graphics. ASA Statistical Computing & Graphics Newsletter , 17(2), 4–7. PDF .
Munzner, T. (2014), Visualization Analysis and Design , Chapter 10.
Lisa Charlotte Muth (2021). 4-part series of blog posts on choosing color scales. Part 1 ; Part 2 ; Part 3 ; Part 4 .
Lisa Charlotte Muth (2022). A detailed guide to colors in data vis style guides. Blog post .
Treinish, Lloyd A. “Why Should Engineers and Scientists Be Worried About Color?.” IBM Thomas J. Watson Research Center, Yorktown Heights, NY (2009): 46. (pdf )
Ware, C. (2012), Information Visualization: Perception for Design , 3rd ed, Chapters 3 & 4.
Zeileis, A., Murrell, P. and Hornik, K. (2009). Escaping RGBland: Selecting colors for statistical graphics, Computational Statistics & Data Analysis , 53(9), 3259-–3270 (PDF ).
Achim Zeileis, Paul Murrell (2019). HCL-Based Color Palettes in grDevices. R Blog post .
Achim Zeileis et al. (2020). “colorspace: A Toolbox for Manipulating and Assessing Colors and Palettes.” Journal of Statistical Software, 96(1), 1-49. doi:10.18637/jss.v096.i01 .
Coloring Political Statements
POLITIFACT reviews the accuracy of statements by politicians and publishes summaries of the results .
A 2016 post on Daily Kos included a visualization of the results for a number of politicians.
Kaiser Fung posted a critique at JunkCharts and proposed an alternative.
I scraped the data as of April 11, 2017, from POLITIFACT; they are available here .
if (! file.exists("polfac.dat"))
download.file("https://stat.uiowa.edu/~luke/data/polfac.dat",
"polfac.dat")
pft <- read.table("polfac.dat")
vcp <- prop.table(as.matrix(pft), 1)[, 6 : 1]
colnames(vcp) <- gsub("\\.", " ", colnames(vcp))
head(vcp)
## Pants on Fire False Mostly False Half True Mostly True True
## Trump 0.16279070 0.3281654 0.1989664 0.14470284 0.12403101 0.04134367
## Bachmann 0.26229508 0.3606557 0.1311475 0.09836066 0.06557377 0.08196721
## Cruz 0.06779661 0.2796610 0.3050847 0.12711864 0.16101695 0.05932203
## Gingrich 0.13924051 0.1898734 0.2025316 0.25316456 0.12658228 0.08860759
## Palin 0.09523810 0.3015873 0.1428571 0.14285714 0.09523810 0.22222222
## Santorum 0.08333333 0.2833333 0.2000000 0.21666667 0.11666667 0.10000000The Daily Kos chart is ordered by the percentage of statements that are more false than true. A function to produce a bar chart with a specified color palette:
## lattice version
polbars <- function(col = cm.colors(6)) {
barchart(vcp[order(rowSums(vcp[, 1 : 3])), ], auto.key = TRUE,
par.settings = list(superpose.polygon = list(col = col)))
}
## ggplot version
gvcp <- as.data.frame(vcp) |>
rownames_to_column("Name") |>
pivot_longer(-1, names_to = "Grade", values_to = "prop") |>
mutate(Grade = fct_rev(fct_inorder(Grade)))
nm <- mutate(gvcp, Grade = ordered(Grade)) |>
filter(Grade <= "Half True") |>
group_by(Name) |>
summarize(prop = sum(prop)) |>
arrange(desc(prop)) |>
pull(Name)
gvcp <- mutate(gvcp, Name = factor(Name, nm))
pvcp <- ggplot(gvcp, aes(Name, prop, fill = Grade)) +
geom_col(position = "fill", width = 0.7) +
coord_flip() +
theme(legend.position = "top",
plot.margin = margin(r = 50),
legend.text = element_text(size = 10)) +
scale_y_continuous(labels = scales::percent, expand = c(0, 0)) +
guides(fill = guide_legend(title = NULL, nrow = 1, reverse = TRUE)) +
labs(x = "", y = "")
polbars <- function(col = cm.colors(6))
pvcp + scale_fill_manual(values = rev(col))
polbars()
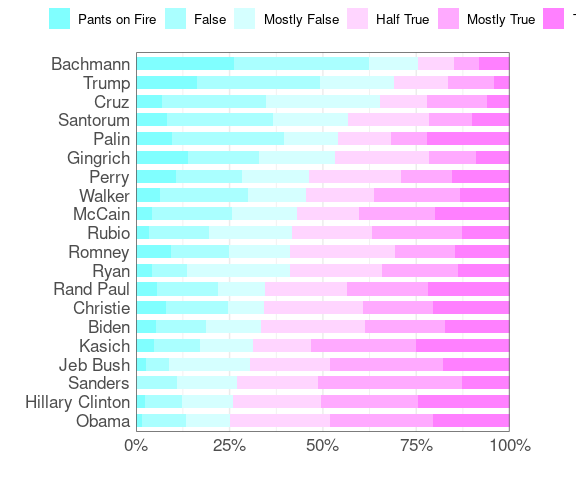
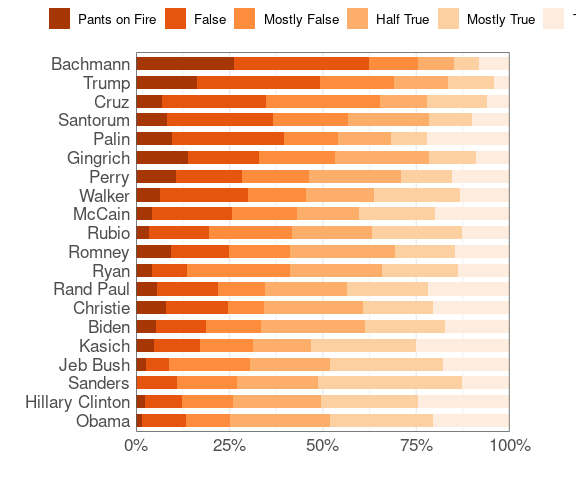
The original Daily Kos chart seems to use a slightly modified version of the Color Brewer Spectral palette, a diverging palette.
polbars(brewer.pal(6, "Spectral"))
dkcols <- brewer.pal(6, "Spectral")
dkcols[4] <- "lightgrey"
polbars(dkcols)
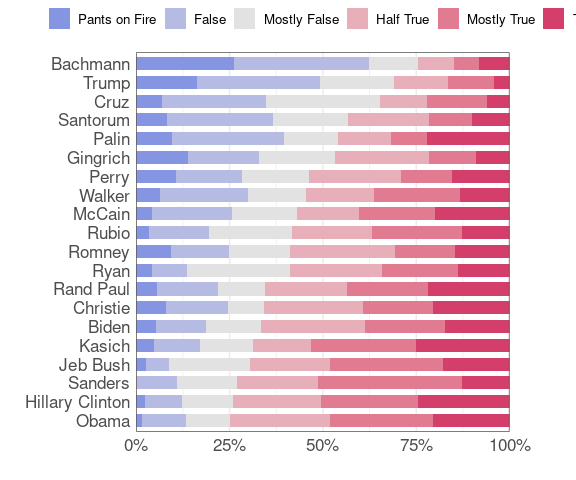
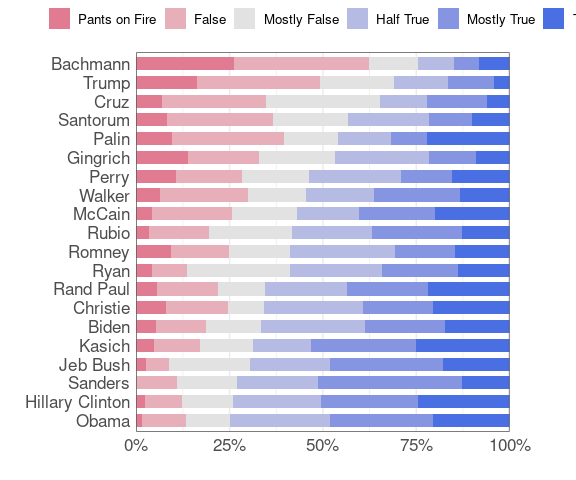
The JunkCharts plot uses another diverging palette, close to the Blue-Red palette available in hclwizard.
rwbcols <- c("#4A6FE3", "#8595E1", "#B5BBE3", "#E2E2E2",
"#E6AFB9", "#E07B91", "#D33F6A")
polbars(rwbcols)
polbars(rev(rwbcols))
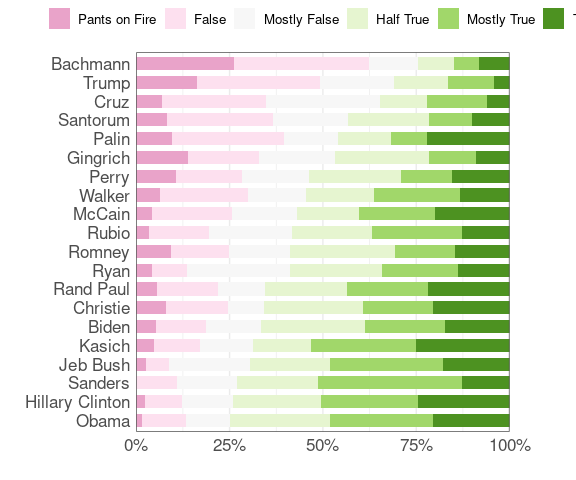
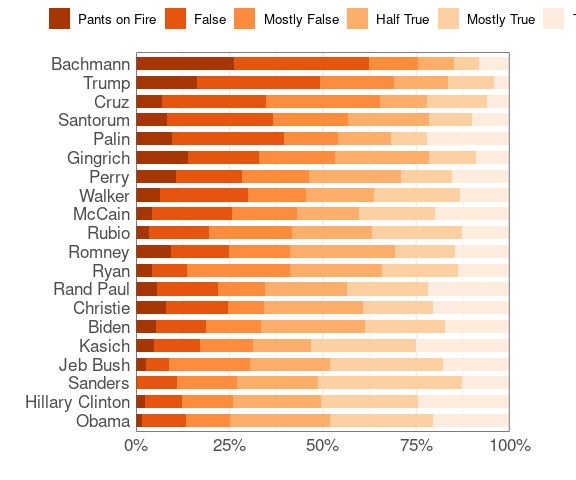
Another diverging palette:
polbars(brewer.pal(7, "PiYG"))
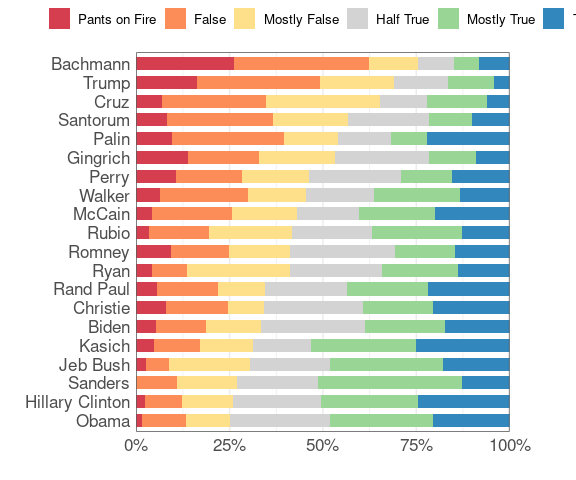
A sequential palette:
polbars(rev(brewer.pal(6, "Oranges")))
Exercises
A color can be specified in hexadecimal notation. Given such a color specification you can find out what it looks like by using it in a simple plot, or by using the Google color picker. Which of the following best describe the color #B22222?
a shade of green
a shade of blue
orange
a shade of red
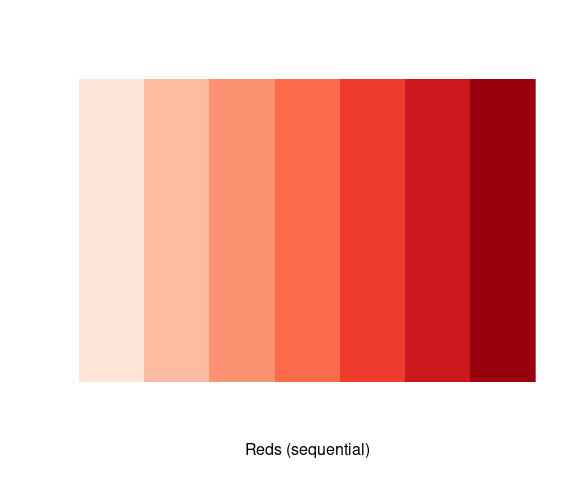
The following shows how to view the colors in the RColorBrewer palette named Reds with 7 colors:
library(RColorBrewer)
display.brewer.pal(7, "Reds")
Which of the following RColorBrewer palettes is diverging?
BluesPuRdSet1RdGy
LS0tCnRpdGxlOiAiQ29sb3IgSXNzdWVzIgpvdXRwdXQ6CiAgaHRtbF9kb2N1bWVudDoKICAgIHRvYzogeWVzCiAgICBjb2RlX2ZvbGRpbmc6IHNob3cKICAgIGNvZGVfZG93bmxvYWQ6IHRydWUKLS0tCgo8bGluayByZWw9InN0eWxlc2hlZXQiIGhyZWY9InN0YXQ0NTgwLmNzcyIgdHlwZT0idGV4dC9jc3MiIC8+CjxzdHlsZSB0eXBlPSJ0ZXh0L2NzcyI+IC5yZW1hcmstY29kZSB7IGZvbnQtc2l6ZTogODUlOyB9IDwvc3R5bGU+CgpgYGB7ciBzZXR1cCwgaW5jbHVkZSA9IEZBTFNFfQpzb3VyY2UoaGVyZTo6aGVyZSgic2V0dXAuUiIpKQpvcHRpb25zKGh0bWx0b29scy5kaXIudmVyc2lvbiA9IEZBTFNFKQpvcHRpb25zKGNvbmZsaWN0cy5wb2xpY3kgPSAiZGVwZW5kcy5vayIpCmtuaXRyOjpvcHRzX2NodW5rJHNldChjb2xsYXBzZSA9IFRSVUUsCiAgICAgICAgICAgICAgICAgICAgICBmaWcuaGVpZ2h0ID0gNSwgZmlnLndpZHRoID0gNiwgZmlnLmFsaWduID0gImNlbnRlciIpCmxpYnJhcnkobGF0dGljZSkKbGlicmFyeSh0aWR5dmVyc2UpCnRoZW1lX3NldCh0aGVtZV9taW5pbWFsKCkgKwogICAgICAgICAgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTYpKSArCiAgICAgICAgICB0aGVtZShwYW5lbC5ib3JkZXIgPSBlbGVtZW50X3JlY3QoY29sb3IgPSAiZ3JleTMwIiwgZmlsbCA9IE5BKSkpCnNldC5zZWVkKDEyMzQ1KQpgYGAKCkNvbG9yIGlzIHZlcnkgZWZmZWN0aXZlIHdoZW4gdXNlZCB3ZWxsLgoKQnV0IHVzaW5nIGNvbG9yIHdlbGwgaXMgbm90IGVhc3kuCgpTb21lIG9mIHRoZSBpc3N1ZXM6CgoqIFBlcmNlcHRpb24gZGVwZW5kcyBvbiBjb250ZXh0LgoKKiBTaW1wbGUgY29sb3IgYXNzaWdubWVudHMgbWF5IG5vdCBzZXBhcmF0ZSBlcXVhbGx5IHdlbGwuCgoqIEVmZmVjdGl2ZW5lc3MgbWF5IHZhcnkgd2l0aCB0aGUgbWVkaXVtIChzY3JlZW4sIHByb2plY3RvciwgcHJpbnQpLgoKKiBTb21lIHBlb3BsZSBkbyBub3QgcGVyY2VpdmUgdGhlIGZ1bGwgc3BlY3RydW0gb2YgY29sb3JzLgoKKiBHcmV5IHNjYWxlIHByaW50aW5nLgoKKiBTb21lIGNvbG9ycyBoYXZlIGN1bHR1cmFsIHNpZ25pZmljYW5jZS4KCiogQ3VsdHVyYWwgc2lnbmlmaWNhbmNlIG1heSB2YXJ5IGFtb25nIGN1bHR1cmVzIGFuZCB3aXRoIHRpbWUuCgoKQW4gaW50ZXJuZXQgImNvbnRyb3ZlcnN5IiBpbiAyMDE1OgpbVGhlIERyZXNzXShodHRwczovL2VuLndpa2lwZWRpYS5vcmcvd2lraS9UaGVfZHJlc3MpIChhbmQgYSBmb2xsb3ctdXAKW2FydGljbGVdKGh0dHBzOi8vd3d3LmluZGVwZW5kZW50LmNvLnVrL2xpZmUtc3R5bGUvZmFzaGlvbi9uZXdzL3RoZS1kcmVzcy1hY3R1YWwtY29sb3VyLWJyYW5kLWFuZC1wcmljZS1kZXRhaWxzLXJldmVhbGVkLTEwMDc0Njg2Lmh0bWwpKQoKCiMjIENvbG9yIFNwYWNlcwoKIyMjIFJHQiBhbmQgSFNWIENvbG9yIFNwYWNlcwoKQ29tcHV0ZXIgbW9uaXRvcnMgYW5kIHByb2plY3RvcnMgd29yayBpbiB0ZXJtcyBvZiByZWQsIGdyZWVuLCBhbmQgYmx1ZQpsaWdodC4KCkFtb3VudHMgb2YgcmVkIGdyZWVuIGFuZCBibHVlIChhbmQgYWxwaGEgbGV2ZWwpIGFyZSBzdG9yZWQgYXMgaW50ZWdlcnMKaW4gdGhlIHJhbmdlIGJldHdlZW4gMCBhbmQgMjU1ICg4LWJpdCBieXRlcykuCgpgYGB7cn0KY29scyA8LSBjKCJyZWQiLCAiZ3JlZW4iLCAiYmx1ZSIsICJ5ZWxsb3ciLCAiY3lhbiIsICJtYWdlbnRhIikKcmdiY29scyA8LSBjb2wycmdiKGNvbHMpOyBjb2xuYW1lcyhyZ2Jjb2xzKSA8LSBjb2xzCnJnYmNvbHMKYGBgCgpDb2xvcnMgYXJlIG9mdGVuIGVuY29kZWQgaW4gX2hleGFkZWNpbWFsXyBmb3JtIChiYXNlIDE2KS4KCmBgYHtyfQpyZ2IoMSwgMCwgMCkgICAjIyBwdXJlIHJlZApyZ2IoMCwgMCwgMSkgICAjIyBwdXJlIGJsdWUKYGBgCgpgYGB7cn0KcmdiKDI1NSwgMCwgMCwgbWF4Q29sb3JWYWx1ZSA9IDI1NSkKcmdiKDAsIDAsIDI1NSwgbWF4Q29sb3JWYWx1ZSA9IDI1NSkKYGBgCgpIdWUsIHNhdHVyYXRpb24sIHZhbHVlIChIU1YpIGlzIGEgc2ltcGxlIHRyYW5zZm9ybWF0aW9uIG9mIFJHQi4KCmBgYHtyfQpyZ2IyaHN2KHJnYmNvbHMpCmBgYAoKSFNWIGlzIGEgbGl0dGxlIG1vcmUgY29udmVuaWVudCBzaW5jZSBpdCBhbGxvd3MgdGhlIGh1ZSB0byBiZQpjb250cm9sbGVkIHNlcGFyYXRlbHkuCgpBIHNpbXBsZSBjb2xvciBwaWNrZXI6IDxodHRwczovL3d3dy5nb29nbGUuY29tL3NlYXJjaD9xPWNvbG9yK3BpY2tlcj4KCkJ1dCBzYXR1cmF0aW9uIGFuZCB2YWx1ZSBhdHRyaWJ1dGVzIGFyZSBub3QgcGFydGljdWxhcmx5IHVzZWZ1bCBmb3IKc3BlY2lmeWluZyBjb2xvcnMgdGhhdCB3b3JrIHdlbGwgcGVyY2VwdHVhbGx5LgoKQSBjb2xvciB3aGVlbCBvZiBmdWxseSBzYXR1cmF0ZWQgY29sb3JzOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQp3aGVlbCA8LSBmdW5jdGlvbihjb2wsIHJhZGl1cyA9IDEsIC4uLikKICAgIHBpZShyZXAoMSwgbGVuZ3RoKGNvbCkpLAogICAgICAgIGNvbCA9IGNvbCwgcmFkaXVzID0gcmFkaXVzLCAuLi4pCndoZWVsKHJhaW5ib3coNikpCmBgYAoKUmVtb3Zpbmcgc2F0dXJhdGlvbjoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShjb2xvcnNwYWNlKQp3aGVlbChkZXNhdHVyYXRlKHJhaW5ib3coNikpKQpgYGAKCkZ1bGx5IHNhdHVyYXRlZCB5ZWxsb3cgaXMgYnJpZ2h0ZXIgdGhhbiByZWQsIHdoaWNoIGlzIGJyaWdodGVyIHRoYW4KYmx1ZS4KCgojIyMgSENMIENvbG9yIFNwYWNlCgpUaGUgX3JhaW5ib3dfIHBhbGV0dGUgb2YgdGhlIGNvbG9yIHdoZWVsIGlzIG9mdGVuIGEgZGVmYXVsdCBpbgp2aXN1YWxpemF0aW9uIHN5c3RlbXMuCgpBIFtibG9nIHBvc3RdKGh0dHBzOi8vd3d3LnplaWxlaXMub3JnL25ld3MvZW5kcmFpbmJvdy8pCmlsbHVzdHJhdGVzIHdoeSB0aGlzIGlzIGEgYmFkIGlkZWEuCgpUaGUgcmFpbmJvdyBodWVzIGFyZSBldmVubHkgc3BhY2VkIGluIHRoZSBjb2xvciBzcGVjdHJ1bSwgYnV0IGNocm9tYQphbmQgbHVtaW5hbmNlIGFyZSBub3QuCgpMdW1pbmFuY2UgaW4gcGFydGljdWxhciBpcyBub3QgbW9ub3RvbmUgYWNyb3NzIHRoZSBwYWxldHRlLgoKYGBge3IsIGZpZy53aWR0aCA9IDEwLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcmdiMmhjbCA8LSBmdW5jdGlvbihjb2wpIHsKICAgICMjIGlnbm9yZXMgYWxwaGEKICAgIGNvbCA8LSBSR0IodChjb2xbMSA6IDMsIF0pIC8gMjU1KQogICAgY29sIDwtIGFzKGNvbCwgInBvbGFyTFVWIikKICAgIGNvbCA8LSB0KGNvbEBjb29yZHNbLCAzIDogMSwgZHJvcCA9IEZBTFNFXSkKICAgIHJvd25hbWVzKGNvbCkgPC0gdG9sb3dlcihyb3duYW1lcyhjb2wpKQogICAgY29sCn0KY29sMmhjbCA8LSBmdW5jdGlvbihjb2wpIHJnYjJoY2woY29sMnJnYihjb2wpKQpwYWwgPC0gZnVuY3Rpb24oY29sLCBib3JkZXIgPSAibGlnaHQgZ3JheSIsIC4uLikgewogICAgbiA8LSBsZW5ndGgoY29sKQogICAgcGxvdCgwLCAwLCB0eXBlID0gIm4iLCB4bGltID0gYygwLCAxKSwgeWxpbSA9IGMoMCwgMSksCiAgICAgICAgIGF4ZXMgPSBGQUxTRSwgeGxhYiA9ICIiLCB5bGFiID0gIiIsIC4uLikKICAgIHJlY3QoKDAgOiAobiAtIDEpKSAvIG4sIDAsICgxIDogbikgLyBuLCAxLCBjb2wgPSBjb2wsIGJvcmRlciA9IGJvcmRlcikKfQoKcGFyKG1mcm93ID0gYygxLCAyKSkKcGFsKHJhaW5ib3coNiksIG1haW4gPSAiU2F0dXJhdGVkIFJhaW5ib3ciKQpwYWwoZGVzYXR1cmF0ZShyYWluYm93KDYpKSwgbWFpbiA9ICJEZXNhdHVyYXRlZCIpCmBgYApgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnNwZWNwbG90KHJhaW5ib3coNiksIGxkdyA9IDQpCmBgYAoKVGhlIGh1ZSwgY2hyb21hLCBsdW1pbmFuY2UKKFtIQ0xdKGh0dHBzOi8vZW4ud2lraXBlZGlhLm9yZy93aWtpL0hDTF9jb2xvcl9zcGFjZSkpIHNwYWNlIGFsbG93cwpzZXBhcmF0ZSBjb250cm9sIG9mOgoKKiBfSHVlXywgdGhlIGNvbG9yLgoKKiBfQ2hyb21hXywgdGhlIGFtb3VudCBvZiB0aGUgY29sb3IuCgoqIF9MdW1pbmFuY2VfLCBvciBwZXJjZWl2ZWQgYnJpZ2h0bmVzcy4KCkhDTCBtYWtlcyBpdCBlYXNpZXIgdG8gY3JlYXRlIHBlcmNlcHR1YWxseSB1bmlmb3JtIGNvbG9yIHBhbGV0dGVzLgoKQSBwYWxldHRlIHdpdGggY29uc3RhbnQgY2hyb21hLCBldmVubHkgc3BhY2VkIGh1ZXMgYW5kIGV2ZW5seSBzcGFjZWQKbHVtaW5hbmNlIHZhbHVlczoKCmBgYHtyLCBmaWcud2lkdGggPSAxMCwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnJhaW42IDwtIGhjbChzZXEoMCwgMzYwICogNSAvIDYsIGxlbiA9IDYpLCA1MCwgc2VxKDYwLCA4MCwgbGVuID0gNikpCnBhcihtZnJvdyA9IGMoMSwgMikpCnBhbChyYWluNiwgbWFpbiA9ICJVbmlmb3JtIFJhaW5ib3ciKQpwYWwoZGVzYXR1cmF0ZShyYWluNiksIG1haW4gPSAiRGVzYXR1cmF0ZWQiKQpgYGAKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0Kc3BlY3Bsb3QocmFpbjYsIGx3ZCA9IDQpCmBgYAoKRm9yIGEgZnVsbHkgc2F0dXJhdGVkIHJlZCwgdmFyeWluZyBvbmx5IGNocm9tYSB0byByZWR1Y2UgdGhlIGFtb3VudCBvZgpjb2xvcjoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcmVkX2hjbCA8LSBsaXN0KGggPSAxMi4xNzM5NSwgYyA9IDE3OS4wNDA3NiwgbCA9IDUzLjI0MDU5KQpzcGVjcGxvdChoY2wocmVkX2hjbCRoLCByZWRfaGNsJGMgKiBzZXEoMCwgMSwgbGVuID0gMTApLCByZWRfaGNsJGwpLCBsd2QgPSA0KQpgYGAKCkZvciBhIGdpdmVuIGh1ZSwgbm90IGFsbCBjb21iaW5hdGlvbnMgb2YgY2hyb21hIGFuZCBsdW1pbmFuY2UgYXJlCnBvc3NpYmxlLgoKSW4gcGFydGljdWxhciwgZm9yIGxvdyBsdW1pbmFuY2UgdmFsdWVzIHRoZSBhdmFpbGFibGUgY2hyb21hIHJhbmdlIGlzCmxpbWl0ZWQuCgpUaGUgW2BnZ3Bsb3RgIGJvb2tdKGh0dHBzOi8vZ2dwbG90Mi1ib29rLm9yZy8pIGNvbnRhaW5zIHRoaXMKdmlzdWFsaXphdGlvbiBvZiB0aGUgSENMIHNwYWNlLgoKKiBIdWUgaXMgbWFwcGVkIHRvIGFuZ2xlLgoqIENocm9tYSBpcyBtYXBwZWQgdG8gcmFkaXVzLgoqIEx1bWluYW5jZSBpcyBtYXBwZWQgdG8gZmFjZXRzLgoKVGhlIG9yaWdpbnMgd2l0aCB6ZXJvIGNocm9tYSBhcmUgc2hhZGVzIG9mIGdyZXkuCgpbSENMIGNvbG9yIHBpY2tlci5dKGh0dHA6Ly9oY2x3aXphcmQub3JnOjMwMDAvaGNsY29sb3JwaWNrZXIvKQoKYGBge3IsIG91dC53aWR0aCA9IDUwMCwgZWNobyA9IEZBTFNFfQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoImdncGxvdDJfaGNsc3BhY2UucG5nIikpCmBgYAoKSENMIGlzIGEgdHJhbnNmb3JtYXRpb24gb2YgdGhlCltDSUVsdXZdKGh0dHBzOi8vZW4ud2lraXBlZGlhLm9yZy93aWtpL0NJRUxVVikgY29sb3Igc3BhY2UgZGVzaWduZWQKZm9yIHBlcmNlcHR1YWwgdW5pZm9ybWl0eS4KClRoZSBkZWZpbml0aW9uIG9mIHRoZSBsdW1pbmFuY2UgdGFrZXMgaW50byBhY2NvdW50IHRoZSBsaWdodApzZW5zaXRpdml0eSBvZiBhIHN0YW5kYXJkIGh1bWFuIG9ic2VydmVyIGF0IHZhcmlvdXMgd2F2ZSBsZW5ndGhzLgoKTGlnaHQgc2Vuc2l0aXZpdHkgZm9yIGRpZmZlcmVudCB3YXZlIGxlbmd0aHMgaW4gZGF5bGlnaHQgY29uZGl0aW9ucwoocGhvdG9waWMgdmlzaW9uKSBhbmQgdW5kZXIgZGFyayBhZGFwdGVkIGNvbmRpdGlvbnMgKHNjb3RvcGljIHZpc2lvbik6Cgo8IS0tCmh0dHA6Ly9saWdodC1tZWFzdXJlbWVudC5jb20vaW1hZ2VzL3NwZWN0cmFsLWx1bWlub3VzLWVmZmljaWVuY3ktZnVuY3Rpb24uanBnCi0tPgoKYGBge3IsIGVjaG8gPSBGQUxTRX0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJsaWdodC1zZW5zaXRpdml0eS5qcGciKSkKYGBgCgo8IS0tCmh0dHBzOi8vd3d3LmhhbmRwcmludC5jb20vSFAvV0NML2NvbG9yMS5odG1sCmh0dHA6Ly9saWdodC1tZWFzdXJlbWVudC5jb20vc3BlY3RyYWwtc2Vuc2l0aXZpdHktb2YtZXllLyAtLT4KCgojIyMgTXVuc2VsbCBDb2xvciBTcGFjZQoKQW5vdGhlciBjb2xvciBzcGFjZSwgc2ltaWxhciB0byBIQ0wsIGlzIHRoZQpbTXVuc2VsbCBzeXN0ZW1dKGh0dHBzOi8vZW4ud2lraXBlZGlhLm9yZy93aWtpL011bnNlbGxfY29sb3Jfc3lzdGVtKQpkZXZlbG9wZWQgaW4gdGhlIGVhcmx5IDE5MDBzLgoKVGhpcyBzeXN0ZW0gdXNlcyBhIEh1ZSwgVmFsdWUsIENocm9tYSBlbmNvZGluZy4KClRoZSBbYG11bnNlbGxgIHBhY2thZ2VdKGh0dHBzOi8vZ2l0aHViLmNvbS9jd2lja2hhbS9tdW5zZWxsKSBwcm92aWRlcwphbiBSIGludGVyZmFjZSBhbmQgaXMgdXNlZCBpbiBgZ2dwbG90YC4KCk11bnNlbGwgc3BlY2lmaWNhdGlvbnMgYXJlIG9mIHRoZSBmb3JtIGAiSCBWL0MiYCwgc3VjaCBhcwpgNVIgNS8xMGAuCgpQb3NzaWJsZSBodWVzIGFyZQoKYGBge3IsIG1lc3NhZ2UgPSBGQUxTRX0KbGlicmFyeShtdW5zZWxsLCBleGNsdWRlID0gImRlc2F0dXJhdGUiKQptbnNsX2h1ZXMoKQpgYGAKCmBWYCBzaG91bGQgYmUgYW4gaW50ZWdlciBiZXR3ZWVuIDAgYW5kIDEwLgoKYENgIHNob3VsZCBiZSBhbiBldmVuIGludGVnZXIgbGVzcyB0aGFuIDI0LCBidXQgbm90IGFsbCBjb21iaW5hdGlvbnMKICBhcmUgcG9zc2libGUuCgpBZGp1c3RpbmcgY29sb3JzIGluIHRoZSB2YWx1ZSwgY2hyb21hLCBhbmQgaHVlIGRpbWVuc2lvbnM6CgpgYGB7ciBtdW5zZWxsLWJsdWVzLCBlY2hvID0gRkFMU0V9Cm15X2JsdWUgPC0gIjVQQiA1LzgiCnBsb3RfbW5zbChjKAogICAgbGlnaHRlcihteV9ibHVlLCAyKSwgICAgICAgICAgICAgIG15X2JsdWUsICBkYXJrZXIobXlfYmx1ZSwgMiksCiAgICBtdW5zZWxsOjpkZXNhdHVyYXRlKG15X2JsdWUsIDIpLCAgbXlfYmx1ZSwgIHNhdHVyYXRlKG15X2JsdWUsIDIpLAogICAgcnlnYnAobXlfYmx1ZSwgMiksICAgICAgICAgICAgICAgIG15X2JsdWUsICBwYmd5cihteV9ibHVlLCAyKSkpCmBgYApgYGB7ciBtdW5zZWxsLWJsdWVzLCBldmFsID0gRkFMU0V9CmBgYAoKQ3JlYXRpbmcgc2NhbGVzOgoKYGBge3IsIHdhcm5pbmc9RkFMU0UsIGZpZy53aWR0aCA9IDgsIGZpZy5oZWlnaHQgPSA0fQpwbG90X21uc2woc2FwcGx5KDAgOiA2LCBkYXJrZXIsIGNvbCA9ICI1UEIgNy80IikpICsgZmFjZXRfd3JhcCh+IG51bSwgbnJvdyA9IDEpCmBgYAoKRXhhbWluaW5nIGF2YWlsYWJsZSBjb2xvcnM6CgpgYGB7ciwgd2FybmluZyA9IEZBTFNFfQpodWVfc2xpY2UoIjVSIikKYGBgCgpgYGB7cn0KdmFsdWVfc2xpY2UoNSkKYGBgCgpDb21wbGVtZW50YXJ5IGNvbG9yczoKCmBgYHtyLCB3YXJuaW5nPUZBTFNFLCBmaWcud2lkdGggPSA4LCBmaWcuaGVpZ2h0ID0gNH0KY29tcGxlbWVudF9zbGljZSgiNVIiKQpgYGAKCiMjIE9wcG9uZW50IFByb2Nlc3MgVGhlb3J5CgpUaGUgX09wcG9uZW50IFByb2Nlc3MgTW9kZWxfIG9mIHZpc2lvbiBzYXlzIHRoYXQgdGhlIGJyYWluIGRpdmlkZXMgdGhlCnZpc3VhbCBzaWduYWwgYW1vbmcgdGhyZWUgb3Bwb3NpbmcgY29udHJhc3QgcGFpcnM6CgoqIGJsYWNrIGFuZCB3aGl0ZTsKCiogcmVkIGFuZCBncmVlbjsKCiogeWVsbG93IGFuZCBibHVlLgoKVGhlIGJsYWNrL3doaXRlIHBhaXIgY29ycmVzcG9uZHMgdG8gbHVtaW5hbmNlIGluIEhDTAoKSHVlIGFuZCBjaHJvbWEgaW4gSENMIHNwYW4gdGhlIHR3byBjaHJvbWF0aWMgYXhlcy4KClRoZSBsdW1pbmFuY2UgYXhpcyBoYXMgaGlnaGVyIHJlc29sdXRpb24gdGhhbiB0aGUgdHdvIGNocm9tYXRpYyBheGVzLgoKVGhlIG1ham9yIGZvcm0gb2YgY29sb3IgdmlzaW9uIGRlZmljaWVuY3kgcmVmbGVjdHMgYW4gaW5hYmlsaXR5IHRvCmRpc3Rpbmd1aXNoIGRpZmZlcmVuY2VzIGFsb25nIHRoZSByZWQvZ3JlZW4gYXhpcy4KCkltcGFpcm1lbnQgYWxvbmcgdGhlIHllbGxvdy9ibHVlIGF4aXMgZG9lcyBvY2N1ciBhcyB3ZWxsIGJ1dCBpcyBtdWNoCnJhcmVyLgoKCiMjIENvbnRyYXN0IGFuZCBDb21wYXJpc29ucwoKVmlzaW9uIHJlYWN0cyB0byBkaWZmZXJlbmNlcywgbm90IGFic29sdXRlcy4KCiogQ29udHJhc3QgaXMgdmVyeSBpbXBvcnRhbnQuCgoqIENvbnRleHQgaXMgdmVyeSBpbXBvcnRhbnQuCgpTbWFsbCBkaWZmZXJlbmNlcyBpbiBzaGFkaW5nIG9yIGh1ZSBjYW4gYmUgcmVjb2duaXplZCB3aGVuIG9iamVjdHMgYXJlCmNvbnRpZ3VvdXMgYnV0IGJlIG11Y2ggaGFyZGVyIHRvIHNlZSB3aGVuIHRoZXkgYXJlIHNlcGFyYXRlZC4KCiFbXShodHRwczovL29wZW5pLm5sbS5uaWguZ292L2ltZ3MvNTEyLzM5OS8zODUyMDA0L1BNQzM4NTIwMDRfMTQ3MS0yMTA1LTE0LVMxNS1TMTItMi5wbmcpCgpfU2ltdWx0YW5lb3VzIGJyaWdodG5lc3MgY29udHJhc3RfOiBhIGdyZXkgcGF0Y2ggb24gYSBkYXJrIGJhY2tncm91bmQKbG9va3MgbGlnaHRlciB0aGFuIHRoZSBzYW1lIGdyZXkgcGF0Y2ggb24gYSBsaWdodCBiYWNrZ3JvdW5kLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwbG90KDAsIDAsIHR5cGUgPSAibiIsIHhsaW0gPSBjKDAsIDEpLCB5bGltID0gYygwLCAxKSwKICAgICBheGVzID0gRkFMU0UsIHhsYWIgPSAiIiwgeWxhYiA9ICIiKQpyZWN0KDAsIDAsIDAuNSwgMSwgY29sID0gImxpZ2h0Z3JleSIsIGJvcmRlciA9IE5BKQpyZWN0KDAuNSwgMCwgMSwgMSwgY29sID0gImRhcmtncmV5IiwgYm9yZGVyID0gTkEpCnJlY3QoMC4yLCAwLjMsIDAuMywgMC43LCBjb2wgPSAiZ3JleSIsIGJvcmRlciA9IE5BKQpyZWN0KDAuNywgMC4zLCAwLjgsIDAuNywgY29sID0gImdyZXkiLCBib3JkZXIgPSBOQSkKYGBgCgpBbiBleGFtcGxlIHdlIHNhdyBlYXJsaWVyOgoKIVtdKGByIElNRygiY2hlc3MxLnBuZyIpYCkgIVtdKGByIElNRygiY2hlc3MyLnBuZyIpYCkKClNvbWUgbW9yZSBhcmUgYXZhaWxhYmxlCltoZXJlXShodHRwczovL2Jsb2cucmV2b2x1dGlvbmFuYWx5dGljcy5jb20vMjAxOC8wOC9sdW1pbmFuY2UtaWxsdXNpb24uaHRtbCksCmluY2x1ZGluZzoKCmBgYHtyLCBlY2hvID0gRkFMU0V9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygibHVtaW5hbmltLmdpZiIpKQpgYGAKCjwhLS0gVHJ5aW5nIGZvciBjb2xvciBjb250cmFzdCBhcyBpbiBXYXJlIEZpZyA0LjE1IG9uIHAgMTE1IGJ1dCBub3QKZ2V0dGluZyB0aGVyZSAtLT4KCmBgYHtyLCBldmFsID0gRkFMU0UsIGVjaG8gPSBGQUxTRX0KcGxvdCgwLCAwLCB0eXBlID0gIm4iLCB4bGltID0gYygwLCAxKSwgeWxpbSA9IGMoMCwgMSksCiAgICAgYXhlcyA9IEZBTFNFLCB4bGFiID0gIiIsIHlsYWIgPSAiIikKcmVjdCgwLCAwLCAwLjUsIDEsIGNvbCA9IGhjbCgwKSwgYm9yZGVyID0gTkEpCnJlY3QoMC41LCAwLCAxLCAxLCBjb2wgPSBoY2woMTIwKSwgYm9yZGVyID0gTkEpCnBpbmsxIDwtIHJnYigxLCAxOTIgLyAyNTUsIDIyMCAvIDI1NSkKcmVjdCgwLjIsIDAuMywgMC4zLCAwLjcsIGNvbCA9IHBpbmsxLCBib3JkZXIgPSBOQSkKcmVjdCgwLjcsIDAuMywgMC44LCAwLjcsIGNvbCA9IHBpbmsxLCBib3JkZXIgPSBOQSkKYGBgCgpVc2luZyBsdW1pbmFuY2Ugb3IgZ3JleSBzY2FsZSBhbG9uZSBkb2VzIG5vdCB3b3JrIHdlbGwgZm9yIGVuY29kaW5nCmNhdGVnb3JpY2FsIHZhcmlhYmxlcyBhZ2FpbnN0IGEga2V5LgoKR3JleSBzY2FsZSBjYW4gYmUgZWZmZWN0aXZlIGZvciBzaG93aW5nIGNvbnRpbnVvdXMgdHJhbnNpdGlvbnMgaW4KcHNldWRvLWNvbG9yIGltYWdlcy4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZmlsbGVkLmNvbnRvdXIodm9sY2FubywgY29sb3IucGFsZXR0ZSA9IGdyZXkuY29sb3JzKQpgYGAKCkdyZXkgc2NhbGUgaXMgbGVzcyBlZmZlY3RpdmUgZm9yIHNlZ21lbnRlZCBtYXBzLCBvciBjaG9yb3BsZXRoIG1hcHM7Cm9ubHkgYSBmZXcgbGV2ZWxzIGNhbiBiZSBhY2N1cmF0ZWx5IGRlY29kZWQuCgoKIyMgSW50ZXJhY3Rpb25zIHdpdGggU2l6ZSwgQmFja2dyb3VuZCBhbmQgUHJveGltaXR5CgpgYGB7ciwgZWNobyA9IEZBTFNFLCBldmFsID0gRkFMU0V9CmxpYnJhcnkobGF0dGljZUV4dHJhKQpsaWJyYXJ5KG1hcHByb2opCmRhdGEoVVNDYW5jZXJSYXRlcykKbWFwcGxvdChyb3duYW1lcyhVU0NhbmNlclJhdGVzKSB+IGxvZyhyYXRlLm1hbGUpLCBkYXRhID0gVVNDYW5jZXJSYXRlcywKICAgICAgICAjI2NvbHJhbXAgPSBncmV5LmNvbG9ycywKICAgICAgICBib3JkZXIgPSBOQSwKICAgICAgICBtYXAgPSBtYXAoImNvdW50eSIsIHBsb3QgPSBGQUxTRSwgZmlsbCA9IFRSVUUsCiAgICAgICAgICAgICAgICAgIHByb2plY3Rpb24gPSAibWVyY2F0b3IiKSkKYGBgCgpGb3Igc21hbGwgaXRlbXMgbW9yZSBjb250cmFzdCBhbmQgbW9yZSBzYXR1cmF0ZWQgY29sb3JzIGFyZSBuZWVkZWQ6CgpgYGB7ciwgZmlnLmhlaWdodCA9IDcsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQp4IDwtIHJ1bmlmKDYsIDAuMSwgMC45KQp5IDwtIHJ1bmlmKDYsIDAuMSwgMC45KQpjb2xzIDwtIGMoInJlZCIsICJncmVlbiIsICJibHVlIiwgInllbGxvdyIsICJjeWFuIiwgIm1hZ2VudGEiKQpmIDwtIGZ1bmN0aW9uKHNpemUgPSAxLCBibGFjayA9IEZBTFNFKSB7CiAgICBwbG90KHgsIHksIHR5cGUgPSAibiIsIHhsaW0gPSBjKDAsIDEpLCB5bGltID0gYygwLCAxKSkKICAgIGlmIChibGFjaykgcmVjdCgwLCAwLCAxLCAxLCBjb2wgPSAiYmxhY2siKQogICAgdGV4dCh4LCB5LCBjb2xzLCBjb2wgPSBjb2xzLCBjZXggPSBzaXplKQp9Cm9wYXIgPC0gcGFyKG1mcm93ID0gYygyLCAyKSkKZigxKQpmKDQpCmYoMSwgVFJVRSkKZig0LCBUUlVFKQpwYXIob3BhcikKYGBgCgpWYXJpYXRpb25zIGluIGx1bWluYW5jZSBhcmUgcGFydGljdWxhcmx5IGhlbHBmdWwgZm9yIHNlZWluZyBmaW5lCnN0cnVjdHVyZSwgc3VjaCBhcyBzbWFsbCB0ZXh0IG9yIHNtYWxsIHN5bWJvbHM6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnBsb3QoMCwgdHlwZSA9ICJuIiwgeGxpbSA9IGMoMCwgMSksIHlsaW0gPSBjKDAsIDEpLAogICAgIGF4ZXMgPSBGQUxTRSwgeGxhYiA9ICIiLCB5bGFiID0gIiIpCnJlY3QoMCwgMCwgMSwgMSwgY29sID0gaGNsKDApKSAjIyBkZWZhdWx0czogYyA9IDM1LCBsID0gODUKcWJmIDwtICJUaGUgcXVpY2sgYnJvd24gZm94IGp1bXBzIC4uLiIKdGV4dCgwLjUsIDAuMywgbGFiZWwgPSBxYmYsIGNvbCA9IGhjbCgxODApKSAgICAgICAjIyBodWUKdGV4dCgwLjUsIDAuNSwgbGFiZWwgPSBxYmYsIGNvbCA9IGhjbCgwLCBjID0gNzApKSAjIyBjaHJvbWEKdGV4dCgwLjUsIDAuNywgbGFiZWwgPSBxYmYsIGNvbCA9IGhjbCgwLCBsID0gNTApKSAjIyBsdW1pbmFuY2UKYGBgCgpDaHJvbWluYW5jZSAoaHVlIGFuZCBjaHJvbWEpIGRpZmZlcmVuY2VzIGFsb25lIGFyZSBub3Qgc3VmZmljaWVudCBmb3IKc21hbGwgaXRlbXMuCgpXYXJlIHJlY29tbWVuZHMgYSBsdW1pbmFuY2UgY29udHJhc3Qgb2YgYXQgbGVhc3QgMzoxIGZvciBzbWFsbCB0ZXh0OwoxMDoxIGlzIHByZWZlcmFibGUuCgpTbWFsbCBhcmVhcyBhbHNvIG5lZWQgdmFyaWF0aW9uIGluIG1vcmUgdGhhbiBodWU6CgpgYGB7ciwgZWNobyA9IEZBTFNFfQpwbG90KDAsIDAsIHR5cGUgPSAibiIsIHhsaW0gPSBjKDAsIDEpLCB5bGltID0gYygwLCAxKSwKICAgICBheGVzID0gRkFMU0UsIHhsYWIgPSAiIiwgeWxhYiA9ICIiKQoKcGFsMCA8LSBmdW5jdGlvbihjb2wsIGJvdHRvbSA9IDAsIHRvcCA9IDEpIHsKICAgIG4gPC0gbGVuZ3RoKGNvbCkKICAgIHJlY3QoKDAgOiAobiAtIDEpKSAvIG4sIGJvdHRvbSwKICAgICAgICAgKDEgOiBuKSAvIG4sIHRvcCwgY29sID0gY29sLCBib3JkZXIgPSAibGlnaHRncmV5IikKfQoKcGFsMChyYWluYm93X2hjbCg4KSwgMCwgMC4yKQpwYWwwKHJhaW5ib3dfaGNsKDgpLCAwLjMsIDAuMzEpCnBhbDAocmFpbmJvdyg4KSwgMC41LCAwLjcpCnBhbDAocmFpbmJvdyg4KSwgMC44LCAwLjgxKQpgYGAKCkNvbnRyYXN0aW5nIGJvcmRlcnMgY2FuIGhlbHAgZm9yIGxhcmdlciBhcmVhcyB3aXRoIHNpbWlsYXIgbHVtaW5hbmNlOgoKKiBvdXRsaW5lcyBvbiB0ZXh0OwoKKiBib3JkZXJzIG9uIHN5bWJvbHM7CgoqIGJvcmRlcnMgb24gcmVnaW9ucywgZS5nIGluIFttYXBzXShodHRwczovL2NvbG9yYnJld2VyMi5vcmcpCgpgYGB7ciwgZmlnLndpZHRoID0gMTAsIGVjaG8gPSBGQUxTRX0KTiA8LSBucm93KHRyZWVzKQpvcCA8LSBwYWxldHRlKHJhaW5ib3coTiwgZW5kID0gMC45KSkKZiA8LSBmdW5jdGlvbihmZywgbWFpbiA9ICIiKQogICAgd2l0aCh0cmVlcywKICAgICAgICAgc3ltYm9scyhIZWlnaHQsIFZvbHVtZSwgY2lyY2xlcyA9IEdpcnRoIC8gMTYsCiAgICAgICAgICAgICAgICAgaW5jaGVzID0gRkFMU0UsIGJnID0gMSA6IE4sCiAgICAgICAgICAgICAgICAgZmcgPSBmZywgbWFpbiA9IG1haW4pKQpwYXIobWZyb3cgPSBjKDEsIDIpKQpmKE5BLCAiTm8gQm9yZGVycyIpCmYoImdyYXkzMCIsICJHcmV5IEJvcmRlcnMiKQpwYWxldHRlKG9wKQpgYGAKCgojIyBDb2xvciBTcGVjaWZpY2F0aW9uIGluIFIKCmBgYHtyLCBpbmNsdWRlID0gRkFMU0V9Cm5jb2xzIDwtIGxlbmd0aChjb2xvcnMoKSkKYGBgCgpBIGxhcmdlIG51bWJlciBvZiBfbmFtZWQgY29sb3JzXyBhcmUgYXZhaWxhYmxlIChjdXJyZW50bHkgYHIgbmNvbHNgKS4KClNvbWUgZXhhbXBsZXM6CmBgYHtyfQpjb2wycmdiKCJyZWQiKQpjb2wycmdiKCJmb3Jlc3RncmVlbiIpCmNvbDJyZ2IoImRlZXBza3libHVlIikKY29sMnJnYigiZmlyZWJyaWNrIikKYGBgCgpUaGVzZSB3aWxsIHNob3cgc29tZSBkZXRhaWxzOgoKYGBge3IsIGV2YWwgPSBGQUxTRX0KY29sb3JzKCkKZGVtbyhjb2xvcnMpCmBgYAoKVGhlIGF2YWlsYWJsZSBuYW1lZCBjb2xvcnMgZm9sbG93IGEgd2lkZWx5IHVzZWQKW3N0YW5kYXJkXShodHRwczovL3d3dy53M3NjaG9vbHMuY29tL2NvbG9ycy9jb2xvcnNfeDExLmFzcCkuCgpUaGVzZSBjb2xvcnMgaW5jbHVkZSB0aGUgMTQwIFtfd2ViCmNvbG9yc19dKGh0dHBzOi8vaHRtbGNvbG9yY29kZXMuY29tL2NvbG9yLW5hbWVzLykgc3VwcG9ydGVkIG9uIG1vZGVybgpicm93c2Vycy4KCkluZGl2aWR1YWwgY29sb3JzIGNhbiBhbHNvIGJlIHNwZWNpZmllZCB1c2luZyBgcmdiKClgIG9yIGBoY2woKWAgb3IgYXMKaGV4YWRlY2ltYWwgc3BlY2lmaWNhdGlvbnMuCgpgYGB7cn0KbGlicmFyeShjb2xvcnNwYWNlKQpoZXgyUkdCKCIjRkYwMDAwIikKYGBgCgpVc2luZyBjb2xvciBzcGFjZXM6CgpgYGB7cn0KcmdiKDEsIDAsIDApCnJnYigyNTUsIDAsIDAsIG1heCA9IDI1NSkKcmdiMmhzdihjb2wycmdiKCJyZWQiKSkKYGBgCgpDb252ZXJ0aW5nIHRvIEhDTDoKYGBge3J9CnJnYjJoY2wgPC0gZnVuY3Rpb24oY29sKSB7CiAgICAjIyBpZ25vcmVzIGFscGhhCiAgICBjb2wgPC0gUkdCKHQoY29sWzEgOiAzLCBdKSAvIDI1NSkKICAgIGNvbCA8LSBhcyhjb2wsICJwb2xhckxVViIpCiAgICBjb2wgPC0gdChjb2xAY29vcmRzWywgMyA6IDEsIGRyb3AgPSBGQUxTRV0pCiAgICByb3duYW1lcyhjb2wpIDwtIHRvbG93ZXIocm93bmFtZXMoY29sKSkKICAgIGNvbAp9CmNvbDJoY2wgPC0gZnVuY3Rpb24oY29sKSByZ2IyaGNsKGNvbDJyZ2IoY29sKSkKCmNvbDJoY2woInJlZCIpCmNvbDJoY2woImdyZWVuIikKY29sMmhjbCgiYmx1ZSIpCmNvbDJoY2woInllbGxvdyIpCmNvbDJoY2woImN5YW4iKQpjb2wyaGNsKCJtYWdlbnRhIikKCmhjbCgxMi4xNywgMTc5LjA0LCA1My4yNCkKYGBgCgpDb2xvciBwaWNrZXJzIGNhbiBoZWxwOgoKKiBHb29nbGUgc2VhcmNoOiBodHRwczovL3d3dy5nb29nbGUuY29tL3NlYXJjaD9xPWNvbG9yK3BpY2tlcgoKKiBgY29sb3VyUGlja2VyKClgIGluIHRoZSAgYGNvbG91cnBpY2tlcmAgcGFja2FnZS4KCldoZW4gYSBzZXQgb2YgY29sb3JzIGlzIG5lZWRlZCB0byBlbmNvZGUgdmFyaWFibGUgdmFsdWVzIGl0IGlzIHVzdWFsbHkKYmVzdCB0byB1c2UgYSBzdWl0YWJsZSBfcGFsZXR0ZV8uCgoKIyMgQ29sb3IgUGFsZXR0ZXMKCl9Db2xvciBwYWxldHRlc18gYXJlIGNvbGxlY3Rpb25zIG9mIGNvbG9ycyB0aGF0IHdvcmsgd2VsbCB0b2dldGhlci4KCkl0IGlzIHVzZWZ1bCB0byBkaXN0aW5ndWlzaCB0aHJlZSBraW5kcyBvZiBwYWxldHRlczoKCiogcXVhbGl0YXRpdmUvY2F0ZWdvcmljYWwgcGFsZXR0ZXM7CgoqIHNlcXVlbnRpYWwgcGFsZXR0ZXM7CgoqIGRpdmVyZ2luZyBwYWxldHRlcy4KClRvb2xzIGZvciBzZWxlY3RpbmcgcGFsZXR0ZXMgaW5jbHVkZToKCiogW0NvbG9yQnJld2VyXShodHRwczovL2NvbG9yYnJld2VyMi5vcmcpOyBhdmFpbGFibGUgaW4gdGhlCiAgYFJDb2xvckJyZXdlcmAgcGFja2FnZS4KCiogW0hDTCBXaXphcmRdKGh0dHBzOi8vaGNsd2l6YXJkLm9yZy8pOyBhbHNvIGF2YWlsYWJsZSBhcyBgaGNsd2l6YXJkYAogIGluIHRoZSBgY29sb3JzcGFjZWAgcGFja2FnZS4KCkEKICBbYmxvZyBwb3N0XShodHRwczovL2Zsb3dpbmdkYXRhLmNvbS8yMDE4LzA0LzEyL3Zpc3VhbGl6YXRpb24tY29sb3ItcGlja2VyLWJhc2VkLW9uLXBlcmNlcHRpb24tcmVzZWFyY2gvKQogIHdpdGggc29tZSBmdXJ0aGVyIG9wdGlvbnMuCgpTb21lIFtjdXJyZW50IFVTIGdvdmVybm1lbnQKICB3b3JrXShodHRwczovL2Rlc2lnbnN5c3RlbS5kaWdpdGFsLmdvdi9jb21wb25lbnRzL2NvbG9ycy8pIG9uIGNvbG9yCiAgcGFsZXR0ZXM7IFttb3JlIGV4dGVuc2l2ZQogIG5vdGVzXShodHRwczovL3hkZ292LmdpdGh1Yi5pby9kYXRhLWRlc2lnbi1zdGFuZGFyZHMvY29tcG9uZW50cy9jb2xvcnMpCiAgYW5kIFtjb2RlXShodHRwczovL2dpdGh1Yi5jb20vdXN3ZHMvdXN3ZHMpLgoKUiBjb2xvciBwYWxldHRlIGZ1bmN0aW9uczoKCiogYHJhaW5ib3coKWAKKiBgaGVhdC5jb2xvcnMoKWAKKiBgdGVycmFpbi5jb2xvcnMoKWAKKiBgdG9wby5jb2xvcnMoKWAKKiBgY20uY29sb3JzKClgCiogYGdyZXkuY29sb3JzKClgCiogYGdyYXkuY29sb3JzKClgCgpUaGVzZSBhbGwgdGFrZSB0aGUgbnVtYmVyIG9mIGNvbG9ycyBhcyBhbiBhcmd1bWVudCwgYXMgd2VsbCBhcyBzb21lCmFkZGl0aW9uYWwgb3B0aW9uYWwgYXJndW1lbnRzLgoKVGhlIGBoY2wuY29sb3IoKWAgZnVuY3Rpb24gcHJvdmlkZXMgYWNjZXNzIHRvIHRoZSBwYWxldHRlcyBkZWZpbmVkIGluCnRoZSBgY29sb3JzcGFjZWAgcGFja2FnZS4KCmBjb2xvclJhbXBQYWxldHRlKClgIGNhbiBiZSB1c2VkIHRvIGNyZWF0ZSBhIF9wYWxldHRlIGZ1bmN0aW9uXyB0aGF0CmludGVycG9sYXRlcyBiZXR3ZWVuIGEgc2V0IG9mIGNvbG9ycyB1c2luZwoKKiBSR0Igc3BhY2Ugb3IgTGFiIChzaW1pbGFyIHRvIEhDTCkgc3BhY2U7CgoqIGxpbmVhciBvciBzcGxpbmUgaW50ZXJwb2xhdGlvbi4KCmBgYHtyfQpyd2IgPC0gY29sb3JSYW1wUGFsZXR0ZSgKICAgIGMoInJlZCIsICJ3aGl0ZSIsICJibHVlIikpCnJ3Yig1KQpgYGAKYGBge3IgcGFsZXR0ZS1mdW5jdGlvbi1leGFtcGxlLCBldmFsID0gRkFMU0V9CmZpbGxlZC5jb250b3VyKHZvbGNhbm8sCiAgICAgICAgICAgICAgIGNvbG9yLnBhbGV0dGUgPSByd2IsCiAgICAgICAgICAgICAgIGFzcCA9IDEpCmBgYApgYGB7ciBwYWxldHRlLWZ1bmN0aW9uLWV4YW1wbGUsIGVjaG8gPSBGQUxTRX0KYGBgCgpXaXRoIG1vcmUgcGVyY2VwdHVhbGx5IGNvbXBhcmFibGUgZXh0cmVtZXMgKGZyb20gdGhlIEJsdWUtUmVkIHBhbGV0dGUKb2YgSENMIFdpemFyZCk6CgpgYGB7ciBwYWxldHRlLWZ1bmN0aW9uLW11dGVkMSwgZXZhbCA9IEZBTFNFfQpyd2IxIDwtIGNvbG9yUmFtcFBhbGV0dGUoCiAgICBjKCIjOEUwNjNCIiwgIndoaXRlIiwgIiMwMjNGQTUiKSkKZmlsbGVkLmNvbnRvdXIodm9sY2FubywKICAgICAgICAgICAgICAgY29sb3IucGFsZXR0ZSA9IHJ3YjEsCiAgICAgICAgICAgICAgIGFzcCA9IDEpCmBgYApgYGB7ciBwYWxldHRlLWZ1bmN0aW9uLW11dGVkMSwgZWNobyA9IEZBTFNFfQpgYGAKCkFuIGFsdGVybmF0aXZlIHVzZXMgdGhlIGBtdXRlZGAgZnVuY3Rpb24gZnJvbSBwYWNrYWdlIGBzY2FsZXNgOgoKYGBge3IgcGFsZXR0ZS1mdW5jdGlvbi1tdXRlZDIsIGV2YWwgPSBGQUxTRX0KcndiMiA8LSBjb2xvclJhbXBQYWxldHRlKAogICAgYyhzY2FsZXM6Om11dGVkKCJyZWQiKSwKICAgICAgIndoaXRlIiwKICAgICAgc2NhbGVzOjptdXRlZCgiYmx1ZSIpKSkKZmlsbGVkLmNvbnRvdXIodm9sY2FubywKICAgICAgICAgICAgICAgY29sb3IucGFsZXR0ZSA9IHJ3YjIsCiAgICAgICAgICAgICAgIGFzcCA9IDEpCmBgYApgYGB7ciBwYWxldHRlLWZ1bmN0aW9uLW11dGVkMiwgZWNobyA9IEZBTFNFfQpgYGAKCk1vc3QgYmFzZSBhbmQgYGxhdHRpY2VgIGZ1bmN0aW9ucyBhbGxvdyBhIHZlY3RvciBvZiBjb2xvcnMgdG8gYmUKc3BlY2lmaWVkLgoKU29tZSwgbGlrZSBgZmlsbGVkLmNvbnRvdXIoKWAgYW5kIGBsZXZlbHBsb3QoKWAgYWxsb3cgYSBwYWxldHRlIGZ1bmN0aW9uCnRvIGJlIHByb3ZpZGVkLgoKYGdncGxvdGAgcHJvdmlkZXMgYSBmcmFtZXdvcmsgZm9yIHNwZWNpZnlpbmcgcGFsZXR0ZSBmdW5jdGlvbnMgdG8gdXNlCndpdGggYHNjYWxlX2NvbG9yX3h5eigpYCBhbmQgYHNjYWxlX2ZpbGxfeHl6KClgIGZ1bmN0aW9ucy4KClBhY2thZ2VzIGxpa2UgYGNvbG9yc3BhY2VgIGFuZCBgdmlyaWRpc2AgcHJvdmlkZSBhZGRpdGlvbmFsCmBzY2FsZV9jb2xvcl94eXooKWAgYW5kIGBzY2FsZV9maWxsX3h5eigpYCBmdW5jdGlvbnMuCgoKIyMgUkNvbG9yQnJld2VyIFBhbGV0dGVzCgpUaGUgYXZhaWxhYmxlIHBhbGV0dGVzOgoKYGBge3IgYnJld2VyLXBhbGxldGVzLCBldmFsID0gRkFMU0V9CmxpYnJhcnkoUkNvbG9yQnJld2VyKQpkaXNwbGF5LmJyZXdlci5hbGwoKQpgYGAKUGFsZXR0ZXMgaW4gdGhlIGZpcnN0IGdyb3VwIGFyZSBfc2VxdWVudGlhbF8uCgpUaGUgc2Vjb25kIGdyb3VwIGFyZSBfcXVhbGl0YXRpdmVfLgoKVGhlIHRoaXJkIGdyb3VwIGFyZSBfZGl2ZXJnaW5nXy4KYGBge3IgYnJld2VyLXBhbGxldGVzLCBlY2hvID0gRkFMU0UsIGZpZy53aWR0aCA9IDgsIGZpZy5oZWlnaHQgPSA4fQpgYGAKClRoZSBgIkJsdWVzImAgIHBhbGV0dGU6CgpgYGB7ciBibHVlcy1wYWxldHRlLCBldmFsID0gRkFMU0V9CmRpc3BsYXkuYnJld2VyLnBhbCg5LCAiQmx1ZXMiKQpgYGAKYGBge3IgYmx1ZXMtcGFsZXR0ZSwgZWNobyA9IEZBTFNFfQpgYGAKCkFzIFJHQiB2YWx1ZXM6CgpgYGB7cn0KYnJld2VyLnBhbCg5LCAiQmx1ZXMiKQpgYGAKClRoZSBwYWxldHRlcyBhcmUgbGltaXRlZCB0byBhIG1heGltdW0gbnVtYmVyIG9mIGxldmVscy4KClRvIG9idGFpbiBtb3JlIGxldmVscyB5b3UgY2FuIGludGVycG9sYXRlLgoKYGBge3J9CmJyZXdlci5wYWwoMTAsICJCbHVlcyIpCgpwYnJibCA8LSBjb2xvclJhbXBQYWxldHRlKGJyZXdlci5wYWwoOSwgIkJsdWVzIiksIGludGVycG9sYXRlID0gInNwbGluZSIpCnBicmJsCnBicmJsKDEwKQpgYGAKCgojIyBDb2xvcnNwYWNlIFBhbGV0dGVzCgpUaGUgYGNvbG9yc3BhY2VgIHBhY2thZ2UgcHJvdmlkZXMgYSB3aWRlIHJhbmdlIG9mIHByZS1kZWZpbmVkIHBhbGV0dGVzOgoKYGBge3IsIGZpZy53aWR0aCA9IDEwfQpsaWJyYXJ5KGNvbG9yc3BhY2UpCmhjbF9wYWxldHRlcyhwbG90ID0gVFJVRSkKYGBgCgpBIHBhcnRpY3VsYXIgbnVtYmVyIG9mIGNvbG9ycyBmcm9tIG9uZSBvZiB0aGVzZSBwYWxldHRlcyBjYW4gYmUKb2J0YWluZWQgd2l0aAoKYGBge3J9CnF1YWxpdGF0aXZlX2hjbCg0LCBwYWxldHRlID0gIkRhcmsgMyIpCmBgYAoKVGhlIGZ1bmN0aW9ucyBgc2VxdWVudGlhbF9oY2woKWAgYW5kIGBkaXZlcmdpbmdfaGNsKClgIGFyZSBhbmFsb2dvdXMuCgpGb3IgdXNlIHdpdGggYGdncGxvdDJgIHRoZSBwYWNrYWdlIHByb3ZpZGVzIHNjYWxlIGZ1bmN0aW9ucyBsaWtlCmBzY2FsZV9maWxsX2Rpc2NyZXRlX3F1YWxpdGF0aXZlKClgIGFuZApgc2NhbGVfY29sb3JfY29udGludW91c19zZXF1ZW50aWFsKClgLgoKQSBbcGFja2FnZQp2aWduZXR0ZV0oaHR0cHM6Ly9jcmFuLnItcHJvamVjdC5vcmcvcGFja2FnZT1jb2xvcnNwYWNlL3ZpZ25ldHRlcy9jb2xvcnNwYWNlLmh0bWwpCnByb3ZpZGVzIG1vcmUgZGV0YWlscyBhbmQgYmFja2dyb3VuZC4KCgojIyBWaXJpZGlzIFBhbGV0dGVzCgpgYGB7ciwgbWVzc2FnZSA9IEZBTFNFLCBlY2hvID0gRkFMU0V9Cm5fY29sIDwtIDEyOAppbWcgPC0gZnVuY3Rpb24ob2JqLCBuYW0pIHsKICBpbWFnZShzZXFfYWxvbmcob2JqKSwgMSwgYXMubWF0cml4KHNlcV9hbG9uZyhvYmopKSwgY29sID0gb2JqLAogICAgICAgIG1haW4gPSBuYW0sIHlsYWIgPSAiIiwgeGF4dCA9ICJuIiwgeWF4dCA9ICJuIiwgIGJ0eSA9ICJuIikKfQoKbGlicmFyeSh2aXJpZGlzKQoKcGFyKG1mcm93ID0gYyg4LCAxKSwgbWFyID0gcmVwKDEsIDQpKQppbWcocmV2KHZpcmlkaXMobl9jb2wpKSwgInZpcmlkaXMiKQppbWcocmV2KG1hZ21hKG5fY29sKSksICJtYWdtYSIpCmltZyhyZXYocGxhc21hKG5fY29sKSksICJwbGFzbWEiKQppbWcocmV2KGluZmVybm8obl9jb2wpKSwgImluZmVybm8iKQppbWcocmV2KGNpdmlkaXMobl9jb2wpKSwgImNpdmlkaXMiKQppbWcocmV2KG1ha28obl9jb2wpKSwgIm1ha28iKQppbWcocmV2KHJvY2tldChuX2NvbCkpLCAicm9ja2V0IikKaW1nKHJldih0dXJibyhuX2NvbCkpLCAidHVyYm8iKQpgYGAKClRoZXNlIGFyZSBwcm92aWRlZCBpbiBwYWNrYWdlIGB2aXJpZGlzTGl0ZWAuCgpQYWxldHRlIGZ1bmN0aW9ucyBhcmUgYHZpcmlkaXMoKWAsIGBtYWtvKClgLCBldGMuLgoKVGhleSBhcmUgYWxzbyBhdmFpbGFibGUgdmlhIHRoZSBgaGNsLmNvbG9ycygpYCBmdW5jdGlvbi4KCkZvciB1c2UgaW4gYGdncGxvdGAgdGhleSBjYW4gYmUgc3BlY2lmaWVkIGluIHRoZSB2aXJpZGlzIGNvbG9yIHNjYWxlCmZ1bmN0aW9ucy4KCgojIyBQYWxldHRlcyBpbiBSIEdyYXBoaWNzCgpgYGB7ciwgZWNobyA9IEZBTFNFfQppZiAoISBmaWxlLmV4aXN0cygiUGxheWZhaXIuZGF0IikpCiAgICBkb3dubG9hZC5maWxlKCJodHRwOi8vd3d3LnN0YXQudWlvd2EuZWR1L35sdWtlL2RhdGEvUGxheWZhaXIiLAogICAgICAgICAgICAgICAgICAiUGxheWZhaXIuZGF0IikKClBsYXlmYWlyIDwtIHJlYWQudGFibGUoIlBsYXlmYWlyLmRhdCIpClBsYXlmYWlyJGNpdHkgPC0gcm93bmFtZXMoUGxheWZhaXIpCnJvd25hbWVzKFBsYXlmYWlyKSA8LSBOVUxMCmBgYAoKPCEtLQpTcGVjaWZ5aW5nIGEgdmVjdG9yIG9mIGNvbG9ycyBpbiBiYXNlIGFuZCBgbGF0dGljZWAgZ3JhcGhpY3M6CgpgYGB7ciwgZXZhbCA9IEZBTFNFfQp3aXRoKFBsYXlmYWlyLCBwbG90KHBvcHVsYXRpb24sIGNvbCA9IHJhaW5ib3cobGVuZ3RoKHBvcHVsYXRpb24pKSkpCndpdGgoUGxheWZhaXIsIHBsb3QocG9wdWxhdGlvbiwgY29sID0gcmFpbmJvdygyKSkpCndpdGgoUGxheWZhaXIsIGJhcnBsb3QocG9wdWxhdGlvbiwgY29sID0gcmFpbmJvdyhsZW5ndGgocG9wdWxhdGlvbikpKSkKd2l0aChQbGF5ZmFpciwgYmFycGxvdChwb3B1bGF0aW9uLCBjb2wgPSByYWluYm93KDIpKSkKCndpdGgoUGxheWZhaXIsCiAgICAgYmFyY2hhcnQocmVvcmRlcihjaXR5LCBwb3B1bGF0aW9uKSB+IHBvcHVsYXRpb24sCiAgICAgICAgICAgICAgY29sID0gcmFpbmJvdyhsZW5ndGgocG9wdWxhdGlvbikpKSkKd2l0aChQbGF5ZmFpciwKICAgICBiYXJjaGFydChyZW9yZGVyKGNpdHksIHBvcHVsYXRpb24pIH4gcG9wdWxhdGlvbiwgY29sID0gcmFpbmJvdygyKSkpCmBgYAoKQSBiZXR0ZXIgYXBwcm9hY2ggZm9yIGBsYXR0aWNlYCBpcyB0byB1c2UgYHBhci5zZXR0aW5nc2A7IHRoaXMgd2lsbAptYWtlIHN1cmUgYSBsZWdlbmQgaXMgY29uc2lzdGVudCB3aXRoIHRoZSBwbG90IGNvbG9ycy4KCmBmaWxsZWQuY29udG91cmAgYW5kIGBsZXZlbHBsb3RgIGFsc28gYWNjZXB0IGEgcGFsZXR0ZSBmdW5jdGlvbjoKCmBgYHtyLCBldmFsID0gRkFMU0V9CmZpbGxlZC5jb250b3VyKHZvbGNhbm8sIGNvbG9yLnBhbGV0dGUgPSB0ZXJyYWluLmNvbG9ycykKbGV2ZWxwbG90KHZvbGNhbm8sIGNvbC5yZWdpb25zID0gdGVycmFpbi5jb2xvcnMpCmBgYAotLT4KCmBnZ3Bsb3RgIHVzZXMgYHNjYWxlX2NvbG9yX3h5eigpYCBvciBgc2NhbGVfZmlsbF94eXooKWAuCgpGb3IgZGlzY3JldGUgc2NhbGVzIHRoZSBjaG9pY2VzIGZvciBgeHl6YCBpbmNsdWRlCgoqIGBodWVgIHZhcmllcyB0aGUgaHVlIChkZWZhdWx0IGZvciB1bm9yZGVyZWQgZmFjdG9ycyk7CiogYGdyZXlgIHVzZXMgZ3JleSBzY2FsZTsKKiBgYnJld2VyYCB1c2VzIENvbG9yQnJld2VyIHBhbGV0dGVzOwoqIGBtYW51YWxgIGFsbG93cyBleHBsaWNpdCBzcGVjaWZpY2F0aW9uLgoqIGB2aXJpZGlzX2RgIGZvciBhbiBhbHRlcm5hdGl2ZSBwYWxldHRlIGZhbWlseSAoZGVmYXVsdCBmb3Igb3JkZXJlciBmYWN0b3JzKS4KCkZvciBjb250aW51b3VzIHNjYWxlcyB0aGUgY2hvaWNlcyBmb3IgYHh5emAgaW5jbHVkZQoKKiBgZ3JhZGllbnRgIGludGVycG9sYXRlcyBiZXR3ZWVuIHR3byBjb2xvcnMsIGxvdyBhbmQgaGlnaDsKKiBgZ3JhZGllbnQyYCBpbnRlcnBvbGF0ZXMgYmV0d2VlbiB0aHJlZSBjb2xvcnMsIGxvdywgbWVkaXVtLCBoaWdoOwoqIGBncmFkaWVudG5gIGludGVycG9sYXRlcyBiZXR3ZWVuIGEgdmVjdG9yIG9mIGNvbG9yczsKKiBgZGlzdGlsbGVyYCBmb3IgQ29sb3JCcmV3ZXIgcGFsZXR0ZXMuCiogYHZpcmlkaXNfY2AgIGZvciBhbiBhbHRlcm5hdGl2ZSBwYWxldHRlIGZhbWlseS4KCk90aGVycyBhcmUgYXZhaWxhYmxlIGluIHBhY2thZ2VzIHN1Y2ggYXMgYGNvbG9yc3BhY2VgLgoKVGhlIGRlZmF1bHQgcXVhbGl0YXRpdmUgYW5kIHNlcXVlbnRpYWwgZGlzY3JldGUgcGFsZXR0ZXM6CgpgYGB7ciwgZmlnLndpZHRoID0gMTAsIGZpZy5oZWlnaHQgPSA0LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShnYXBtaW5kZXIpCmdhcF8yMDA3IDwtIGZpbHRlcihnYXBtaW5kZXIsIHllYXIgPT0gMjAwNykgfD4gc2xpY2VfbWF4KHBvcCwgbiA9IDIwKQpwIDwtIG11dGF0ZShnYXBfMjAwNywgY291bnRyeSA9IHJlb3JkZXIoY291bnRyeSwgcG9wKSkgfD4KICAgIGdncGxvdChhZXMoeCA9IGdkcFBlcmNhcCwgeSA9IGxpZmVFeHAsIGZpbGwgPSBjb250aW5lbnQpKSArCiAgICBzY2FsZV9zaXplX2FyZWEobWF4X3NpemUgPSAxMCkgKwogICAgc2NhbGVfeF9sb2cxMCgpICsKICAgIGdlb21fcG9pbnQoc2l6ZSA9IDQsIHNoYXBlID0gMjEpICsKICAgIGd1aWRlcyhmaWxsID0gZ3VpZGVfbGVnZW5kKG92ZXJyaWRlLmFlcyA9IGxpc3Qoc2l6ZSA9IDQpKSkKcDEgPC0gcCArIGdndGl0bGUoIkh1ZSIpCnAyIDwtIHAgKyBzY2FsZV9maWxsX3ZpcmlkaXNfZCgpICsgZ2d0aXRsZSgiVmlyaWRpcyIpCmxpYnJhcnkocGF0Y2h3b3JrKQpwMSArIHAyCmBgYAoKRGlzY3JldGUgZXhhbXBsZXMgZm9yIGBicmV3ZXJgLCBgY29sb3JzcGFjZWAgYW5kIGBtYW51YWxgOgoKYGBge3IsIGZpZy53aWR0aCA9IDksIGZpZy5oZWlnaHQgPSA2LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcDEgPC0gcCArIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiU2V0MSIpICsKICAgIGdndGl0bGUoIkJyZXdlciBTZXQxIikKcDIgPC0gcCArIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiU2V0MiIpICsKICAgIGdndGl0bGUoIkJyZXdlciBTZXQyIikKcDMgPC0gcCArIHNjYWxlX2ZpbGxfZGlzY3JldGVfcXVhbGl0YXRpdmUoIkRhcmsgMyIpICsKICAgIGdndGl0bGUoIkNvbG9yc3BhY2UgRGFyayAzIikKcDQgPC0gcCArIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGMoQWZyaWNhID0gInJlZCIsIEFzaWEgPSAiYmx1ZSIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIEFtZXJpY2FzID0gImdyZWVuIiwgRXVyb3BlID0gImdyZXkiKSkgKwogICAgZ2d0aXRsZSgiTWFudWFsIikKKHAxICsgcDIpIC8gKHAzICsgcDQpCmBgYAoKVGhlIGRlZmF1bHQgZm9yIGNvbnRpbnVvdXMgc2NhbGVzIGlzIGBncmFkaWVudGAgZnJvbSBhIGRhcmsgYmx1ZSB0byBhCmxpZ2h0IGJsdWU6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9ClYgPC0gZGF0YS5mcmFtZSh4ID0gcmVwKHNlcV9sZW4obnJvdyh2b2xjYW5vKSksIG5jb2wodm9sY2FubykpLAogICAgICAgICAgICAgICAgeSA9IHJlcChzZXFfbGVuKG5jb2wodm9sY2FubykpLCBlYWNoID0gbnJvdyh2b2xjYW5vKSksCiAgICAgICAgICAgICAgICB6ID0gYXMudmVjdG9yKHZvbGNhbm8pKQpwIDwtIGdncGxvdChWLCBhZXMoeCwgeSwgZmlsbCA9IHopKSArIGdlb21fcmFzdGVyKCkgKyBjb29yZF9maXhlZCgpCnAKYGBgCgpTb21lIGFsdGVybmF0aXZlczoKCmBgYHtyIGFsdC1jb250aW51b3VzLCBlY2hvID0gRkFMU0UsIGZpZy53aWR0aCA9IDEyLCBmaWcuaGVpZ2h0ID0gOX0KYGBgCmBgYHtyIGFsdC1jb250aW51b3VzLCBldmFsID0gRkFMU0UsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwMSA8LSBwICsgc2NhbGVfZmlsbF9ncmFkaWVudDIoCiAgICAgICAgICAgICAgbG93ID0gInJlZCIsIG1pZCA9ICJ3aGl0ZSIsIGhpZ2ggPSAiYmx1ZSIsCiAgICAgICAgICAgICAgbWlkcG9pbnQgPSBtZWRpYW4odm9sY2FubykpICsKICAgIGdndGl0bGUoIlJlZC1XaGl0ZS1CbHVlIEdyYWRpZW50IikKcDIgPC0gcCArIHNjYWxlX2ZpbGxfdmlyaWRpc19jKCkgKwogICAgZ2d0aXRsZSgiVmlyaWRpcyIpCnAzIDwtIHAgKyBzY2FsZV9maWxsX2dyYWRpZW50bigKICAgICAgICAgICAgICBjb2xvcnMgPSB0ZXJyYWluLmNvbG9ycyg4KSkgKwogICAgZ2d0aXRsZSgiVGVycmFpbiIpCgp2YmlucyA8LSBzZXEoODAsIGJ5ID0gMjAsIGxlbmd0aC5vdXQgPSA3KQpuYyA8LSBsZW5ndGgodmJpbnMpIC0gMQpwNCA8LSBnZ3Bsb3QobXV0YXRlKFYsIHogPSBmY3RfcmV2KGN1dCh6LCB2YmlucykpKSwKICAgICAgICAgICAgIGFlcyh4LCB5LCBmaWxsID0geikpICsKICAgIGdlb21fcmFzdGVyKCkgKwogICAgc2NhbGVfZmlsbF9tYW51YWwodmFsdWVzID0gcmV2KHRlcnJhaW4uY29sb3JzKG5jKSkpICsKICAgIGdndGl0bGUoIkRpc2NyZXRpemVkIFRlcnJhaW4iKQoocDEgKyBwMikgLyAocDMgKyBwNCkKYGBgCgpEaXNjcmV0aXppbmcgYSBjb250aW51b3VzIHJhbmdlIHRvIGEgbW9kZXN0IG51bWJlciBvZiBsZXZlbHMgY2FuIG1ha2UKZGVjb2RpbmcgdmFsdWVzIGZyb20gYSBsZWdlbmQgZWFzaWVyLgoKPCEtLQojIyBmaWxsZWQuY29udG91cih2b2xjYW5vLCBjb2xvci5wYWxldHRlID0gdGVycmFpbi5jb2xvcnMsIG5sZXZlbHMgPSBuYykKLS0+CgoKIyMgUmVkdWNlZCBDb2xvciBWaXNpb24KCkNvbG9yIHZpc2lvbiBkZWZpY2llbmN5IGFmZmVjdHMgYWJvdXQgMTAlIG9mIG1hbGVzLCBhIHNtYWxsZXIKcGVyY2VudGFnZSBvZiBmZW1hbGVzLgoKVGhlIG1vc3QgY29tbW9uIGZvcm0gaXMgcmVkdWNlZCBhYmlsaXR5IHRvIGRpc3Rpbmd1aXNoIHJlZCBhbmQgZ3JlZW4uCgpTb21lIHdlYiBzaXRlcyBwcm92aWRlIHRvb2xzIHRvIHNpbXVsYXRlIGhvdyBhIHZpc3VhbGl6YXRpb24gd291bGQKbG9vayB0byBhIGNvbG9yIHZpc2lvbiBkZWZpY2llbnQgdmlld2VyLgoKVGhlIFIgcGFja2FnZXMgYGRpY2hyb21hdGAsIGBjb2xvcnNwYWNlYCwgYW5kIGBjb2xvcmJsaW5kcmAgcHJvdmlkZQp0b29scyBmb3Igc2ltdWxhdGluZyBob3cgY29sb3JzIHdvdWxkIGxvb2sgdG8gYSBjb2xvciB2aXNpb24gZGVmaWNpZW50CnZpZXdlciBmb3IgdGhyZWUgbWFqb3IgdHlwZXMgb2YgY29sb3IgdmlzaW9uIGRlZmljaWVuY3k6CgoqIGRldXRlcmFub21hbHkgKGdyZWVuIGNvbmUgY2VsbHMgZGVmZWN0aXZlKTsKKiBwcm90YW5vbWFseSAocmVkIGNvbmUgY2VsbHMgZGVmZWN0aXZlKTsKKiB0cml0YW5vbWFseSAoYmx1ZSBjb25lIGNlbGxzIGRlZmVjdGl2ZSkuCgpBbiBhcnRpY2xlIGV4cGxhaW5pbmcgdGhlIGNvbG9yIHZpc2lvbiBpbXBhaXJtZW50IHNpbXVsYXRpb24gaXMKYXZhaWxhYmxlCltoZXJlXShodHRwOi8vY29sb3JzcGFjZS5yLWZvcmdlLnItcHJvamVjdC5vcmcvYXJ0aWNsZXMvY29sb3JfdmlzaW9uX2RlZmljaWVuY3kuaHRtbCkKPCEtLSBodHRwczovL2FyeGl2Lm9yZy9hYnMvMTkwMy4wNjQ5MCAtLT4KClVzaW5nIHNvbWUgdG9vbHMgZnJvbSBwYWNrYWdlcyBgY29sb3JzcGFjZWAgYW5kIGBjb2xvcmJsaW5kZXJgIHdlIGNhbgpzaW11bGF0ZSB3aGF0IGEgcGxvdCB3b3VsZCBsb29rIGxpa2UgaW4gZ3JleSBzY2FsZSBhbmQgdG8gc29tZW9uZQp3aXRoIHNvbWUgb2YgdGhlIG1ham9yIHR5cGVzIG9mIGNvbG9yIGltcGFpcm1lbnQuCgpBIHBsb3Qgd2l0aCB0aGUgZGVmYXVsdCBkaXNjcmV0ZSBjb2xvciBwYWxldHRlOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwIDwtIGdncGxvdChnYXBfMjAwNywgYWVzKGdkcFBlcmNhcCwgbGlmZUV4cCwgY29sb3IgPSBjb250aW5lbnQpKSArCiAgICBnZW9tX3BvaW50KHNpemUgPSA0KSArCiAgICBzY2FsZV94X2xvZzEwKCkgKwogICAgZ3VpZGVzKGNvbG9yID0gZ3VpZGVfbGVnZW5kKG92ZXJyaWRlLmFlcyA9IGxpc3Qoc2l6ZSA9IDQpKSkKcApgYGAKCjwhLS0gIyMgbm9saW50IHN0YXJ0OiBvYmplY3RfdXNhZ2UgLS0+CmBgYHtyIGN2ZC1leGFtcGxlcywgZmlnLndpZHRoID0gOS41LCBmaWcuaGVpZ2h0ID0gNi41LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShjb2xvcmJsaW5kcikKbGlicmFyeShjb2xvcnNwYWNlKQpsaWJyYXJ5KGdyaWQpCmNvbG9yX2NoZWNrIDwtIGZ1bmN0aW9uKHApIHsKICAgIHAxIDwtIGVkaXRfY29sb3JzKHAgKyBnZ3RpdGxlKCJEZXNhdHVyYXRlZCIpLCBkZXNhdHVyYXRlKQogICAgcDIgPC0gZWRpdF9jb2xvcnMocCArIGdndGl0bGUoImRldXRhbiIpLCBkZXV0YW4pCiAgICBwMyA8LSBlZGl0X2NvbG9ycyhwICsgZ2d0aXRsZSgicHJvdGFuIiksIHByb3RhbikKICAgIHA0IDwtIGVkaXRfY29sb3JzKHAgKyBnZ3RpdGxlKCJ0cml0YW4iKSwgdHJpdGFuKQogICAgZ3JpZEV4dHJhOjpncmlkLmFycmFuZ2UocDEsIHAyLCBwMywgcDQsIG5yb3cgPSAyKQp9CmNvbG9yX2NoZWNrKHApCmBgYAo8IS0tICMjIG5vbGludCBlbmQgLS0+CgpGb3IgdGhlIFZpcmlkaXMgcGFsZXR0ZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcHYgPC0gcCArIHNjYWxlX2NvbG9yX3ZpcmlkaXNfZCgpCnB2CmBgYAoKYGBge3IsIGZpZy53aWR0aCA9IDkuNSwgZmlnLmhlaWdodCA9IDYuNSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmNvbG9yX2NoZWNrKHB2KQpgYGAKClRoZSBgc3dhdGNocGxvdCgpYCBmdW5jdGlvbiBpbiB0aGUgYGNvbG9yc3BhY2VgIHBhY2thZ2UgY2FuIGJlIHVzZWQKd2l0aCB0aGUgYGN2ZCA9IFRSVUVgIGFyZ3VtZW50IHRvIHNpbXVsYXRlIGhvdyBzcGVjaWZpYyBwYWxldHRlcyB3b3JrCmZvciBkaWZmZXJlbnQgY29sb3IgdmlzaW9uIGRlZmljaWVuY2llczoKCmBgYHtyfQpjb2xvcnNwYWNlOjpzd2F0Y2hwbG90KHJhaW5ib3coNiksIGN2ZCA9IFRSVUUpCmBgYAoKYGBge3J9CmNvbG9yc3BhY2U6OnN3YXRjaHBsb3QoaGNsLmNvbG9ycyg2KSwgY3ZkID0gVFJVRSkKYGBgCgoKIyMgVHdvIElzc3VlcyB0byBXYXRjaCBPdXQgRm9yCgojIyMgTWlzc2luZyBWYWx1ZXMKCkl0IGlzIGNvbW1vbiBmb3IgZGVmYXVsdCBzZXR0aW5ncyB0byBub3QgYXNzaWduIGEgY29sb3IgZm9yIG1pc3NpbmcgdmFsdWVzLgoKSW4gYSBjaG9yb3BsZXRoIG1hcCB3aXRoIChtYWRlLXVwKSBkYXRhIHdoZXJlIG9uZSBzdGF0ZSdzIHZhbHVlIGlzCm1pc3NpbmcgdGhpcyBtaWdodCBub3QgYmUgbm90aWNlZC4KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbSA8LSBtYXBfZGF0YSgic3RhdGUiKQpkIDwtIGRhdGEuZnJhbWUocmVnaW9uID0gdW5pcXVlKG0kcmVnaW9uKSwKICAgICAgICAgICAgICAgIHZhbCA9IG9yZGVyZWQoc2FtcGxlKDEgOiA0LCA0OSwgcmVwbGFjZSA9IFRSVUUpKSkKbSA8LSBsZWZ0X2pvaW4obSwgZCwgInJlZ2lvbiIpCnBtIDwtIGdncGxvdChtKSArCiAgICBnZW9tX3BvbHlnb24oYWVzKGxvbmcsIGxhdCwgZ3JvdXAgPSBncm91cCwgZmlsbCA9IHZhbCkpICsKICAgIGNvb3JkX21hcCgpICsKICAgIGdndGhlbWVzOjp0aGVtZV9tYXAoKQoKZG5tIDwtIG11dGF0ZShtLCB2YWwgPSByZXBsYWNlKHZhbCwgcmVnaW9uID09ICJtaWNoaWdhbiIsIE5BKSkKcG0gJSslIGRubQpgYGAKVW5sZXNzIHRoZSB2aWV3ZXIgaXMgdmVyeSBmYW1pbGlhciB3aXRoIFVTIGdlb2dyYXBoeS4KCk9yIGlzIGZyb20gTWljaGlnYW4uCgpJbiBhIHNjYXR0ZXJwbG90IHRoZXJlIGFyZSBldmVuIGZld2VyIGN1ZXM6CgpgYGB7ciwgZmlnLndpZHRoID0gMTAsIGZpZy5oZWlnaHQgPSA0LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ25jIDwtIG11dGF0ZShnYXBfMjAwNywgY29udGluZW50ID0gcmVwbGFjZShjb250aW5lbnQsIGNvdW50cnkgPT0gIkNoaW5hIiwgTkEpKQpwdiArCiAgICBwdiAlKyUgZ25jCmBgYAoKU3BlY2lmeWluZyBgbmEudmFsdWUgPSAicmVkImAsIG9yIHNvbWUgb3RoZXIgY29sb3IsIHdpbGwgbWFrZSBzdXJlCmBOQWAgdmFsdWVzIGFyZSB2aXNpYmxlOgoKYGBge3IsIGZpZy53aWR0aCA9IDE0LCBmaWcuaGVpZ2h0ID0gNSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CihwbSAlKyUgZG5tICsKIHNjYWxlX2ZpbGxfdmlyaWRpc19kKG5hLnZhbHVlID0gInJlZCIpICsgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpKSArCiAgICAocHYgJSslIGduYyArIHNjYWxlX2NvbG9yX3ZpcmlkaXNfZChuYS52YWx1ZSA9ICJyZWQiKSkKYGBgCgpVc2luZyBvdXRsaW5lcyBjYW4gYWxzbyBoZWxwOgoKYGBge3IsIGZpZy53aWR0aCA9IDE0LCBmaWcuaGVpZ2h0ID0gNSwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnAxIDwtIHBtICUrJSBkbm0gKwogICAgZ2VvbV9wb2x5Z29uKGFlcyhsb25nLCBsYXQsIGdyb3VwID0gZ3JvdXApLAogICAgICAgICAgICAgICAgIGZpbGwgPSBOQSwgY29sb3IgPSAiYmxhY2siLCBsaW5ld2lkdGggPSAwLjEpICsKICAgIHRoZW1lKGxlZ2VuZC5wb3NpdGlvbiA9ICJ0b3AiKQpwMiA8LSBwdiAlKyUgZ25jICsKICAgIGdlb21fcG9pbnQoc2hhcGUgPSAyMSwgZmlsbCA9IE5BLCBjb2xvciA9ICJibGFjayIsIHNpemUgPSA0KQpwMSArIHAyCmBgYAoKQSBmaW5hbCBwbG90IG1pZ2h0IGhhbmRsZSBtaXNzaW5nIHZhbHVlcyBkaWZmZXJlbnRseSwgYnV0IGZvciBpbml0aWFsCmV4cGxvcmF0aW9ucyBpdCBpcyBhIGdvb2QgaWRlYSB0byBtYWtlIHN1cmUgdGhleSBhcmUgY2xlYXJseSB2aXNpYmxlLgoKCiMjIyBBbGlnbmluZyBEaXZlcmdpbmcgUGFsZXR0ZXMKCkRpdmVyZ2luZyBwYWxldHRlcyBhcmUgdmVyeSB1c2VmdWwgZm9yIHNob3dpbmcgZGV2aWF0aW9ucyBhYm92ZSBvcgpiZWxvdyBhIGJhc2VsaW5lLgoKYGBge3IsIGZpZy5oZWlnaHQgPSAzLCBmaWcud2lkdGggPSA3LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcGFyKG1mcm93ID0gYygxLCAyKSkKUkNvbG9yQnJld2VyOjpkaXNwbGF5LmJyZXdlci5wYWwoNywgIlBSR24iKQpSQ29sb3JCcmV3ZXI6OmRpc3BsYXkuYnJld2VyLnBhbCg2LCAiUFJHbiIpCmBgYAoKRm9yIGEgZGl2ZXJnaW5nIHBhbGV0dGUgdG8gd29yayBwcm9wZXJseSwgdGhlIHBhbGV0dGUgYmFzZSBsaW5lIG5lZWRzCnRvIGJlIGFsaWduZWQgd2l0aCB0aGUgZGF0YSBiYXNlbGluZS4KCkhvdyB0byBkbyB0aGlzIHdpbGwgZGVwZW5kIG9uIHRoZSBwYWxldHRlLCBidXQgeW91IGRvIG5lZWQgdG8ga2VlcAp0aGlzIGluIG1pbmQgd2hlbiB1c2luZyBhIGRpdmVyZ2luZyBwYWxldHRlLgoKSnVzdCB1c2luZyBgc2NhbGVfZmlsbF9icmV3ZXJgIGlzIG5vdCBlbm91Z2ggd2hlbiB0aGUgdmFsdWUgcmFuZ2UgaXMKbm90IHN5bW1ldHJpYyBhcm91bmQgdGhlIGJhc2VsaW5lOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQptIDwtIG1hcF9kYXRhKCJzdGF0ZSIpCmQgPC0gZGF0YS5mcmFtZShyZWdpb24gPSB1bmlxdWUobSRyZWdpb24pLAogICAgICAgICAgICAgICAgdmFsID0gb3JkZXJlZChzYW1wbGUoKDEgOiA2KSAtIDMsIDQ5LCByZXBsYWNlID0gVFJVRSkpKQptIDwtIGxlZnRfam9pbihtLCBkLCAicmVnaW9uIikKcCA8LSBnZ3Bsb3QobSkgKwogICAgZ2VvbV9wb2x5Z29uKGFlcyhsb25nLCBsYXQsIGdyb3VwID0gZ3JvdXAsIGZpbGwgPSB2YWwpKSArCiAgICBjb29yZF9tYXAoKSArCiAgICBnZ3RoZW1lczo6dGhlbWVfbWFwKCkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInJpZ2h0IikKcCArIHNjYWxlX2ZpbGxfYnJld2VyKHBhbGV0dGUgPSAiUFJHbiIpCmBgYAoKU2V0dGluZyB0aGUgc2NhbGUgbGltaXRzIGV4cGxpY2l0bHkgZm9yY2VzIGEgNy1jYXRlZ29yeSBzeW1tZXRyaWMgc2NhbGUKdGhhdCBhbGlnbnMgdGhlIHplcm8gdmFsdWUgd2l0aCB0aGUgbWlkZGxlIGNvbG9yOgoKYGBge3IsIHdhcm5pbmcgPSBGQUxTRX0KbGltcyA8LSBhcy5jaGFyYWN0ZXIoLTMgOiAzKQpwICsgc2NhbGVfZmlsbF9icmV3ZXIocGFsZXR0ZSA9ICJQUkduIiwKICAgICAgICAgICAgICAgICAgICAgIGxpbWl0cyA9IGxpbXMpCmBgYAoKVGhpcyBzaG93cyBhIGNhdGVnb3J5IGluIHRoZSBsZWdlbmQgZm9yIC0zIHRoYXQgZG9lcyBub3QgYXBwZWFyIGluIHRoZSBtYXAuCgpUaGlzIGlzIG9mdGVuIHdoYXQgeW91IHdhbnQuCgpCdXQgaWYgeW91IHdhbnQgdG8gZHJvcCB0aGUgLTMgY2F0ZWdvcnksIG9uZSBvcHRpb24gaXMgdG8gdXNlIGEgbWFudWFsCnNjYWxlOgoKYGBge3J9CnZhbHMgPC0gUkNvbG9yQnJld2VyOjpicmV3ZXIucGFsKDcsICJQUkduIikKbmFtZXModmFscykgPC0gbGltcwpwICsgc2NhbGVfZmlsbF9tYW51YWwodmFsdWVzID0gdmFsc1stMV0pCmBgYAoKCiMjIEJpdmFyaWF0ZSBQYWxldHRlcwoKSXQgaXMgcG9zc2libGUgdG8gZW5jb2RlIHR3byB2YXJpYWJsZXMgaW4gYSBwYWxldHRlLgoKU29tZSBzYW1wbGUgcGFsZXR0ZXM6CgpgYGB7ciwgZWNobyA9IEZBTFNFfQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoImJpdnBhbC5wbmciKSkKYGBgCgpCaXZhcmlhdGUgcGFsZXR0ZXMgYXJlIHNvbWV0aW1lcyB1c2VkIGluIFtiaXZhcmlhdGUgY2hvcm9wbGV0aAptYXBzXShodHRwczovL3d3dy5qb3NodWFzdGV2ZW5zLm5ldC9jYXJ0b2dyYXBoeS9tYWtlLWEtYml2YXJpYXRlLWNob3JvcGxldGgtbWFwLykuCgpTb21lIHJlY29tbWVuZGF0aW9ucyBmcm9tIEN5bnRoaWEgQnJld2VyIGFyZSBhdmFpbGFibGUKW2hlcmVdKGh0dHBzOi8vd2ViLmFyY2hpdmUub3JnL3dlYi8yMDIxMDQxNTE2MTA0OS9odHRwOi8vd3d3LnBlcnNvbmFsLnBzdS5lZHUvY2FiMzgvQ29sb3JTY2gvU2NoZW1lcy5odG1sKS4KCkEKW2Rpc2N1c3Npb25dKGh0dHBzOi8vanVua2NoYXJ0cy50eXBlcGFkLmNvbS9qdW5rX2NoYXJ0cy8yMDIzLzA0L2JpdmFyaWF0ZS1jaG9yb3BsZXRocy5odG1sKQpvZiBhIHJlY2VudCBleGFtcGxlLgoKVW5sZXNzIG9uZSB2YXJpYWJsZSBpcyBiaW5hcnksIGFuZCB0aGUgcGFsZXR0ZSBpcyB2ZXJ5IHdlbGwgY2hvc2VuLCBpdAppcyBoYXJkIHRvIGRlY29kZSBhIHZpc3VhbGl6YXRpb24gdXNpbmcgYSBiaW5hcnkgcGFsZXR0ZSB3aXRob3V0CmNvbnN0YW50bHkgcmVmZXJyaW5nIHRvIHRoZSBrZXkuCgoKIyMgQ3VsdHVyZSwgVHJhZGl0aW9uLCBhbmQgQ29udmVudGlvbnMKCkNvbG9ycyBjYW4gaGF2ZSBkaWZmZXJlbnQgbWVhbmluZ3MgaW4gZGlmZmVyZW50IGN1bHR1cmVzIGFuZCBhdApkaWZmZXJlbnQgdGltZXMuCgoqIEEgW3Zpc3VhbAogIHJlcHJlc2VudGF0aW9uXShodHRwczovL3d3dy5pbmZvcm1hdGlvbmlzYmVhdXRpZnVsLm5ldC92aXN1YWxpemF0aW9ucy9jb2xvdXJzLWluLWN1bHR1cmVzLykKCiogQSBbYmxvZwogIHBvc3RdKGh0dHBzOi8vd3d3Lmh1ZmZwb3N0LmNvbS9lbnRyeS93aGF0LWNvbG9ycy1tZWFuLWluLW90aGVyX2JfOTA3ODY3NCkKICBhdCB0aGUgSHVmZmluZ3RvbiBQb3N0LgoKKiBBIFtzaW1pbGFyCiAgcG9zdF0oaHR0cHM6Ly93d3cuc2h1dHRlcnN0b2NrLmNvbS9ibG9nL2NvbG9yLXN5bWJvbGlzbS1hbmQtbWVhbmluZ3MtYXJvdW5kLXRoZS13b3JsZCkKICBhdCBTaHV0dGVyc3RvY2suCgpDb252ZW50aW9ucyBjYW4gYWxzbyBnaXZlIGNvbG9ycyBwYXJ0aWN1bGFyIG1lYW5pbmdzOgoKKiByZWQvZ3JlZW4gaW4gdHJhZmZpYyBsaWdodHM7CgoqIHJlZC9ncmVlbiBjb2xvcnMgaW4gbWljcm9hcnJheSBoZWF0bWFwczsKCiogcmVkIHN0YXRlcyBhbmQgYmx1ZSBzdGF0ZXM7CgoqIHBpbmsgZm9yIGJyZWFzdCBjYW5jZXI7CgoqIHBpbmsgZm9yIGdpcmxzLCBibHVlIGZvciBib3lzOwoKKiBibGFjayBmb3IgbW91cm5pbmcuCgoKIyMjIFRyYWZmaWMgTGlnaHRzCgpbVHJhZmZpYwogIGxpZ2h0c10oaHR0cHM6Ly93d3cuYXV0b2V2b2x1dGlvbi5jb20vbmV3cy9hdXRvbW90aXZlLXdpa2ktd2h5LWFyZS10cmFmZmljLWxpZ2h0cy1yZWQteWVsbG93LWFuZC1ncmVlbi00MjU1Ny5odG1sKQogIHVzZSByZWQvZ3JlZW4sIGV2ZW4gdGhvdWdoIHRoaXMgaXMgYSBtYWpvciBheGlzIG9mIGNvbG9yIHZpc2lvbgogIGRlZmljaWVuY3kuCgpUaGUgY29udmVudGlvbiBjb21lcyBmcm9tIHJhaWxyb2Fkcy4KClRoZSByZWQgdXNlZCBnZW5lcmFsbHkgY29udGFpbnMgc29tZSBvcmFuZ2UgYW5kIHRoZSBncmVlbiBjb250YWlucwpibHVlIHRvIGhlbHAgd2l0aCByZWQvZ3JlZW4gY29sb3IgdmlzaW9uIGRlZmljaWVuY3kuCgpQb3NpdGlvbiBwcm92aWRlcyBhbiBhbHRlcm5hdGUgZW5jb2RpbmcuIE9yaWVudGF0aW9ucyBkbyB2YXJ5LgoKPCEtLQpodHRwOi8vcmdiLnRvL2tleXdvcmQvMTc3NzkvMS90cmFmZmljLWxpZ2h0LWdyZWVuCmh0dHA6Ly9lbmN5Y29sb3JwZWRpYS5jb20vY2MwNjA1CgpodHRwczovL3d3dy5hdXRvZXZvbHV0aW9uLmNvbS9uZXdzL2F1dG9tb3RpdmUtd2lraS13aHktYXJlLXRyYWZmaWMtbGlnaHRzLXJlZC15ZWxsb3ctYW5kLWdyZWVuLTQyNTU3Lmh0bWwKaHR0cHM6Ly93d3cudGhyaWxsaXN0LmNvbS9jYXJzL25hdGlvbi90cmFmZmljLWxpZ2h0LWNvbG9ycy1oaXN0b3J5Ci0tPgoKIyMjIE1pY3JvYXJyYXkgSGVhdG1hcHMKCi0gW01pY3JvYXJyYXlzXShodHRwczovL2VuLndpa2lwZWRpYS5vcmcvd2lraS9ETkFfbWljcm9hcnJheSkgYXJlIHVzZWQKICBmb3IgdGhlIGFuYWx5c2lzIG9mIGdlbmUtbGV2ZWwgY2hhbmdlcyBhbmQgZGlmZmVyZW5jZXMgaW4KICBiaW8tbWVkaWNhbCByZXNlYXJjaC4KLSBEeWVzIGFyZSB1c2VkIHRoYXQgcmVzdWx0IGluIGdlbmVzIHdpdGggYSBoaWdoIHJlc3BvbnNlIGFwcGVhcmluZyByZWQKICBhbmQgZ2VuZXMgd2l0aCBhIGxvdyByZXNwb25zZSBhcHBlYXJpbmcgZ3JlZW4uCi0gSW4ga2VlcGluZyB3aXRoIHRoaXMgcGh5c2ljYWwgY2hhcmFjdGVyaXN0aWMgb2YgbWljcm9hcnJheXMsIGEKICBjb21tb24gdmlzdWFsaXphdGlvbiBvZiB0aGUgZGF0YSBpcyBhcyBhIHJlZC9ncmVlbiBoZWF0IG1hcC4KCjwhLS0KaHR0cHM6Ly93d3ctdGMucGJzLm9yZy93Z2JoL25vdmEvZWR1Y2F0aW9uL2FjdGl2aXRpZXMvcGRmLzM0MTNfZ2VuZXNfMDIucGRmCmh0dHBzOi8vYmlvcmFtYmxlLndvcmRwcmVzcy5jb20vMjAxNS8wOC8wMy9oZWF0bWFwcy1wYXJ0LTMtaG93LXRvLWNyZWF0ZS1hLW1pY3JvYXJyYXktaGVhdG1hcC13aXRoLXIvCi0tPgoKCiMjIyBSZWQgU3RhdGVzIGFuZCBCbHVlIFN0YXRlcwoKSXQgaXMgbm93IHN0YW5kYXJkIGluIHRoZSBVUyB0byByZWZlciB0byBSZXB1YmxpY2FuLWxlYW5pbmcgc3RhdGVzIGFzCnJlZCBzdGF0ZXMgYW5kIERlbW9jcmF0LWxlYW5pbmcgc3RhdGVzIGFzIGJsdWUgc3RhdGVzLgoKVGhpcyBpcyBhIGZhaXJseSByZWNlbnQgY29udmVudGlvbiwgZGF0aW5nIGJhY2sgdG8gdGhlIDIwMDAKcHJlc2lkZW50aWFsIGVsZWN0aW9uLgoKUHJpb3IgdG8gMTk4MCBpdCB3YXMgc29tZXdoYXQgbW9yZSB0cmFkaXRpb25hbCB0byB1c2UgcmVkIGZvciBtb3JlCmxlZnQtbGVhbmluZyBEZW1vY3JhdHMuCgpBIG1hcCBvZiB0aGUgMTk2MCBlbGVjdGlvbiByZXN1bHRzIHVzZXMgdGhlc2UgbW9yZSB0cmFkaXRpb25hbCBjb2xvcnMuCgpgYGB7ciwgZWNobyA9IEZBTFNFfQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoImUxOTYwX2VjbWFwLkdJRiIpKQpgYGAKCkluIDE5OTYgdGhlIF9OZXcgWW9yayBUaW1lc18gdXNlZCBibHVlIGZvciBEZW1vY3JhdCwgcmVkIGZvcgpSZXB1YmxpY2FuLCBidXQgdGhlIF9XYXNoaW5ndG9uIFBvc3RfIHVzZWQgdGhlIG9wcG9zaXRlIGNvbG9yIHNjaGVtZS4KClRoZSBsb25nLCBkcmF3biBvdXQgcHJvY2VzcyBvZiB0aGUgMjAwMCBlbGVjdGlvbiBtYXkgaGF2ZSBjb250cmlidXRlZAp0byBmaXhpbmcgdGhlIGNvbG9yIHNjaGVtYSBhdCB0aGUgY3VycmVudCBjb252ZW50aW9uLgoKCiMjIE5vdGVzCgpQb2ludHMgbmVlZCBtb3JlIHNhdHVyYXRpb24sIGx1bWluYW5jZSB0aGFuIGFyZWFzLgoKRmFsc2UgY29sb3IgaW1hZ2VzIG1heSBiZW5lZml0IGZyb20gZGlzY3JldGl6aW5nLgoKQml2YXJpYXRlIGVuY29kaW5ncyAoZS5nLiBgeCA9IGh1ZSwgeSA9IGx1bWluYW5jZWApIGFyZSBwb3NzaWJsZSBidXQKdHJpY2t5IGFuZCBub3Qgb2Z0ZW4gYSBnb29kIGlkZWEuIEJlc3QgaWYgYXQgbGVhc3Qgb25lIGlzIGJpbmFyeS4KClByb3ZpZGluZyBhIHNlY29uZCBlbmNvZGluZywgZS5nLiBzaGFwZSwgcG9zaXRpb24gY2FuIGhlbHAgZm9yIGNvbG9yCnZpc2lvbiBkZWZpY2llbnQgdmlld2VycyBhbmQgcGhvdG9jb3B5aW5nLgoKSW4gYXJlYSBwbG90cyBhbmQgbWFwcyBpdCBpcyBpbXBvcnRhbnQgdG8gZGlzdGluZ3Vpc2ggYmV0d2VlbiBiYXNlCmxpbmUgdmFsdWVzIGFuZCBtaXNzaW5nIHZhbHVlcy4KCklmIG9ic2VydmVkIHZhbHVlcyBvbmx5IGNvdmVyIHBhcnQgb2YgYSBwb3NzaWJsZSByYW5nZSwgaXQgaXMKc29tZXRpbWVzIGFwcHJvcHJpYXRlIHRvIHVzZSBhIGNvbG9yIGNvZGluZyB0aGF0IGFwcGxpZXMgdG8gdGhlIGVudGlyZQpwb3NzaWJsZSByYW5nZS4KCkZvciBkaXZlcmdpbmcgcGFsZXR0ZXMsIHNvbWUgY2FyZSBtYXkgYmUgbmVlZGVkIHRvIG1ha2Ugc3VyZSB0aGUKbmV1dHJhbCBjb2xvciBhbmQgdGhlIG5ldXRyYWwgdmFsdWUgYXJlIHByb3Blcmx5IGFsaWduZWQuCgpVc2luZyBhIHdlbGwtZGVzaWduZWQgcGFsZXR0ZSBpcyB1c3VhbGx5IGJldHRlciB0aGFuIGNyZWF0aW5nIHlvdXIgb3duLgoKQ2hvb3NpbmcgYSBwYWxldHRlIGNhbiBjb25zaWRlciBtYW55IGZhY3RvcnMsIGluY2x1ZGluZyBhcHBlYXJhbmNlIGFuZCBicmFuZGluZy4KCgojIyBBIFVJIERpdmVyZ2luZyBQYWxldHRlPwoKW1VJIGNvbG9yIGd1aWRlbGluZXNdKGh0dHBzOi8vYnJhbmQudWlvd2EuZWR1L2NvbG9yKSBhcmUgc3BlbGxlZCBvdXQgaW4gdGhlIFticmFuZCBtYW51YWxdKGh0dHBzOi8vYnJhbmQudWlvd2EuZWR1LykuCgpgYGB7cn0KVUlnb2xkIDwtIHJnYigyNTUsIDIwNSwgMCwgbWF4Q29sb3JWYWx1ZT0yNTUpCnBkVUkgPC0gY29sb3JSYW1wUGFsZXR0ZShjKCJibGFjayIsICJ3aGl0ZSIsIFVJZ29sZCkpCmNvbG9yc3BhY2U6OnN3YXRjaHBsb3QocGRVSSg1KSkKYGBgCgpgYGB7cn0KY29sb3JzcGFjZTo6c3dhdGNocGxvdChwZFVJKDUpLCBjdmQgPSBUUlVFKQpgYGAKCgojIyBSZWZlcmVuY2VzCgo+IEZldywgU3RlcGhlbi4gIlByYWN0aWNhbCBydWxlcyBmb3IgdXNpbmcgY29sb3IgaW4gY2hhcnRzLiIgVmlzdWFsCj4gQnVzaW5lc3MgSW50ZWxsaWdlbmNlIE5ld3NsZXR0ZXIgMTEKPiAoMjAwOCk6IDI1LiAoW1BERl0oaHR0cDovL3d3dy5wZXJjZXB0dWFsZWRnZS5jb20vYXJ0aWNsZXMvdmlzdWFsX2J1c2luZXNzX2ludGVsbGlnZW5jZS9ydWxlc19mb3JfdXNpbmdfY29sb3IucGRmKSkKCj4gSGFycm93ZXIsIE0uIEEuIGFuZCBCcmV3ZXIsIEMuIE0uICgyMDAzKS4gQ29sb3JCcmV3ZXIub3JnOiBBbiBvbmxpbmUKPiB0b29sIGZvciBzZWxlY3RpbmcgY29sb3Igc2NoZW1lcyBmb3IgbWFwcy4KPiBfVGhlIENhcnRvZ3JhcGhpYyBKb3VybmFsXywgNDAsIDI3LS0zNy4gW0NvbG9yQnJld2VyIHdlYgo+IHNpdGVdKGh0dHBzOi8vY29sb3JicmV3ZXIyLm9yZykuICBUaGUgYFJDb2xvcEJyZXdlcmAgcGFja2FnZSBwcm92aWRlcwo+IGFuIFIgaW50ZXJmYWNlLgoKPiBJaGFrYSwgUi4gKDIwMDMpLiBDb2xvdXIgZm9yIHByZXNlbnRhdGlvbiBncmFwaGljcywgaW4gSy4gSG9ybmlrLAo+IEYuIExlaXNjaCwgYW5kIEEuIFplaWxlaXMgKGVkcy4pLCBbX1Byb2NlZWRpbmdzIG9mIHRoZSAzcmRfCj4gX0ludGVybmF0aW9uYWwgV29ya3Nob3Agb24gRGlzdHJpYnV0ZWQgU3RhdGlzdGljYWxfCj4gX0NvbXB1dGluZ19dKGh0dHBzOi8vd3d3LnItcHJvamVjdC5vcmcvY29uZmVyZW5jZXMvRFNDLTIwMDMvUHJvY2VlZGluZ3MvKSwKPiBWaWVubmEsCj4gQXVzdHJpYS4gW1BERl0oaHR0cHM6Ly93d3cuci1wcm9qZWN0Lm9yZy9jb25mZXJlbmNlcy9EU0MtMjAwMy9Qcm9jZWVkaW5ncy9JaGFrYS5wZGYpLgo+IFNlZSBhbHNvIHRoZSBgY29sb3JzcGFjZWAgcGFja2FnZSBhbmQKPiBbdmlnbmV0dGVdKGh0dHBzOi8vY3Jhbi5yLXByb2plY3Qub3JnL3BhY2thZ2U9Y29sb3JzcGFjZS92aWduZXR0ZXMvaGNsLWNvbG9ycy5wZGYpLgoKPiBMdW1sZXksIFQuICgyMDA2KS4gQ29sb3IgY29kaW5nIGFuZCBjb2xvciBibGluZG5lc3MgaW4gc3RhdGlzdGljYWwKPiBncmFwaGljcy4gIF9BU0EgU3RhdGlzdGljYWwgQ29tcHV0aW5nICYgR3JhcGhpY3MgTmV3c2xldHRlcl8sIDE3KDIpLAo+IDQtLTcuIFtQREZdKGh0dHBzOi8vZHJpdmUuZ29vZ2xlLmNvbS9vcGVuP2lkPTFjZWptdnlHalBubktzTkVTR3VOUVRzWmhsNF92Qm5kRSkuCgo+IE11bnpuZXIsIFQuICgyMDE0KSwgX1Zpc3VhbGl6YXRpb24gQW5hbHlzaXMgYW5kIERlc2lnbl8sIENoYXB0ZXIgMTAuCgo+IExpc2EgQ2hhcmxvdHRlIE11dGggKDIwMjEpLiA0LXBhcnQgc2VyaWVzIG9mIGJsb2cgcG9zdHMgb24gY2hvb3NpbmcKPiBjb2xvciBzY2FsZXMuIFtQYXJ0Cj4gMV0oaHR0cHM6Ly9ibG9nLmRhdGF3cmFwcGVyLmRlL3doaWNoLWNvbG9yLXNjYWxlLXRvLXVzZS1pbi1kYXRhLXZpcy8pOwo+IFtQYXJ0Cj4gMl0oaHR0cHM6Ly9ibG9nLmRhdGF3cmFwcGVyLmRlL3F1YW50aXRhdGl2ZS12cy1xdWFsaXRhdGl2ZS1jb2xvci1zY2FsZXMvKTsKPiBbUGFydAo+IDNdKGh0dHBzOi8vYmxvZy5kYXRhd3JhcHBlci5kZS9kaXZlcmdpbmctdnMtc2VxdWVudGlhbC1jb2xvci1zY2FsZXMvKTsKPiBbUGFydAo+IDRdKGh0dHBzOi8vYmxvZy5kYXRhd3JhcHBlci5kZS9jbGFzc2VkLXZzLXVuY2xhc3NlZC1jb2xvci1zY2FsZXMvKS4KCj4gTGlzYSBDaGFybG90dGUgTXV0aCAoMjAyMikuIEEgZGV0YWlsZWQgZ3VpZGUgdG8gY29sb3JzIGluIGRhdGEgdmlzCj4gc3R5bGUgZ3VpZGVzLiAgW0Jsb2cKPiBwb3N0XShodHRwczovL2Jsb2cuZGF0YXdyYXBwZXIuZGUvY29sb3JzLWZvci1kYXRhLXZpcy1zdHlsZS1ndWlkZXMvKS4KCj4gVHJlaW5pc2gsIExsb3lkIEEuICJXaHkgU2hvdWxkIEVuZ2luZWVycyBhbmQgU2NpZW50aXN0cyBCZSBXb3JyaWVkCj4gQWJvdXQgQ29sb3I/LiIgSUJNIFRob21hcyBKLiBXYXRzb24gUmVzZWFyY2ggQ2VudGVyLCBZb3JrdG93bgo+IEhlaWdodHMsIE5ZICgyMDA5KTogNDYuICAoW3BkZl0oaHR0cHM6Ly93d3cucmVzZWFyY2hnYXRlLm5ldC9wcm9maWxlL0FobWVkX0VsaGF0dGFiMi9wb3N0L1BsZWFzZV9zdWdnZXN0X3NvbWVfZ29vZF8zRF9wbG90X3Rvb2xfU29mdHdhcmVfZm9yX3N1cmZhY2VfcGxvdC9hdHRhY2htZW50LzVjMDViYTM1Y2ZlNGE3NjQ1NTA2OTQ4ZS9BUyUzQTY5OTg5NDMzNTU1NzY0NCU0MDE1NDM4NzkyMjE3MjUvZG93bmxvYWQvV2h5K1Nob3VsZCtFbmdpbmVlcnMrYW5kK1NjaWVudGlzdHMrQmUrV29ycmllZCtBYm91dCtDb2xvcl8ucGRmKSkKCj4gV2FyZSwgQy4gKDIwMTIpLCBfSW5mb3JtYXRpb24gVmlzdWFsaXphdGlvbjogUGVyY2VwdGlvbiBmb3IgRGVzaWduXywKPiAzcmQgZWQsIENoYXB0ZXJzIDMKPiAmIDQuCgo+IFplaWxlaXMsIEEuLCBNdXJyZWxsLCBQLiBhbmQgSG9ybmlrLCBLLiAoMjAwOSkuIEVzY2FwaW5nIFJHQmxhbmQ6Cj4gU2VsZWN0aW5nIGNvbG9ycyBmb3Igc3RhdGlzdGljYWwgZ3JhcGhpY3MsIF9Db21wdXRhdGlvbmFsIFN0YXRpc3RpY3MKPiAmIERhdGEgQW5hbHlzaXNfLCA1Myg5KSwgMzI1OS3igJMzMjcwCj4gKFtQREZdKGh0dHBzOi8vd3d3LnplaWxlaXMub3JnL3BhcGVycy9aZWlsZWlzK0hvcm5paytNdXJyZWxsLTIwMDkucGRmKSkuCgo+IEFjaGltIFplaWxlaXMsIFBhdWwgTXVycmVsbCAoMjAxOSkuIEhDTC1CYXNlZCBDb2xvciBQYWxldHRlcyBpbgo+IGBnckRldmljZXNgLiAgW1IgQmxvZwo+IHBvc3RdKGh0dHBzOi8vZGV2ZWxvcGVyLnItcHJvamVjdC5vcmcvQmxvZy9wdWJsaWMvMjAxOS8wNC8wMS9oY2wtYmFzZWQtY29sb3ItcGFsZXR0ZXMtaW4tZ3JkZXZpY2VzL2luZGV4Lmh0bWwpLgoKPiBBY2hpbSBaZWlsZWlzIGV0IGFsLiAoMjAyMCkuIOKAnGNvbG9yc3BhY2U6IEEgVG9vbGJveCBmb3IgTWFuaXB1bGF0aW5nCj4gYW5kIEFzc2Vzc2luZyBDb2xvcnMgYW5kIFBhbGV0dGVzLuKAnSBKb3VybmFsIG9mIFN0YXRpc3RpY2FsIFNvZnR3YXJlLAo+IDk2KDEpLAo+IDEtNDkuIFtkb2k6MTAuMTg2MzcvanNzLnYwOTYuaTAxXShodHRwczovL2RvaS5vcmcvMTAuMTg2MzcvanNzLnYwOTYuaTAxKS4KCgojIyBDb2xvcmluZyBQb2xpdGljYWwgU3RhdGVtZW50cwoKUE9MSVRJRkFDVCByZXZpZXdzIHRoZSBhY2N1cmFjeSBvZiBzdGF0ZW1lbnRzIGJ5IHBvbGl0aWNpYW5zIGFuZApwdWJsaXNoZXMgW3N1bW1hcmllcyBvZiB0aGUKcmVzdWx0c10oaHR0cHM6Ly93d3cucG9saXRpZmFjdC5jb20vcGVyc29uYWxpdGllcy9taWNoZWxlLWJhY2htYW5uLykuCgpBIFsyMDE2CnBvc3RdKGh0dHBzOi8vd3d3LmRhaWx5a29zLmNvbS9zdG9yaWVzLzIwMTYvOC83LzE1NTY2NjYvLVRocmVlLWxlc3NvbnMtZnJvbS10aGUtcmlzZS1vZi1Eb25hbGQtVHJ1bXApCm9uIFtEYWlseSBLb3NdKGh0dHBzOi8vd3d3LmRhaWx5a29zLmNvbS8pIGluY2x1ZGVkIGEKW3Zpc3VhbGl6YXRpb25dKGh0dHBzOi8vaW1hZ2VzLmRhaWx5a29zLmNvbS9pbWFnZXMvMjgzMTUyL2xhcmdlL2RhdGF2aXpfcm9iZXJ0X21hbm4ucG5nPzE0NzAzMjM1MTQpCm9mIHRoZSByZXN1bHRzIGZvciBhIG51bWJlciBvZiBwb2xpdGljaWFucy4KCkthaXNlciBGdW5nIHBvc3RlZCBhCltjcml0aXF1ZV0oaHR0cHM6Ly9qdW5rY2hhcnRzLnR5cGVwYWQuY29tL2p1bmtfY2hhcnRzLzIwMTcvMDQvd2hhdC1kb2VzLWx5aW5nLXBvbGl0aWNpYW5zLWhhdmUtaW4tY29tbW9uLXdpdGgtcmFpbmJvdy1jb2xvcnMuaHRtbCkKYXQgW0p1bmtDaGFydHNdKGh0dHBzOi8vanVua2NoYXJ0cy50eXBlcGFkLmNvbSkgYW5kIHByb3Bvc2VkIGFuCmFsdGVybmF0aXZlLgoKPCEtLQojIyBTY3JhcGluZyB0aGUgZGF0YToKCnBnIDwtIHJlYWRfaHRtbCgiaHR0cHM6Ly93d3cucG9saXRpZmFjdC5jb20vcGVyc29uYWxpdGllcy9taWNoZWxlLWJhY2htYW5uLyIpCmxhYnMgPC0gaHRtbF90ZXh0KGh0bWxfbm9kZXMocGcsIHhwYXRoPSIvL3NwYW5bQGNsYXNzPSdjaGFydGxpc3RfX2xhYmVsJ10iKSkKdm5vZGVzIDwtIGh0bWxfbm9kZXMocGcsIHhwYXRoPSIvL3NwYW5bQGNsYXNzPSdjaGFydGxpc3RfX2luZGV4J10iKQp2dHh0IDwtIGh0bWxfdGV4dCh2bm9kZXMpCmFzLm51bWVyaWMoZ3N1YigiW1xcKFxcKV0iLCAiIiwgdnR4dCkpCnZhdHRyIDwtIGh0bWxfYXR0cih2bm9kZXMsICJzdHlsZSIpCmFzLm51bWVyaWMoc3ViKCIuKjooW1s6ZGlnaXQ6XV0rKS4qIiwgIlxcMSIsIHZhdHRyKSkKCnBvbGZhYyA8LSBmdW5jdGlvbihwaWQpIHsKICAgIHVybCA8LSBzcHJpbnRmKCJodHRwOi8vd3d3LnBvbGl0aWZhY3QuY29tL3BlcnNvbmFsaXRpZXMvJXMvIiwgcGlkKQogICAgcGcgPC0gcmVhZF9odG1sKHVybCkKICAgIGxhYnMgPC0gaHRtbF90ZXh0KGh0bWxfbm9kZXMocGcsIHhwYXRoPSIvL3NwYW5bQGNsYXNzPSdjaGFydGxpc3RfX2xhYmVsJ10iKSkKICAgIHZub2RlcyA8LSBodG1sX25vZGVzKHBnLCB4cGF0aD0iLy9zcGFuW0BjbGFzcz0nY2hhcnRsaXN0X19pbmRleCddIikKICAgIHZ0eHQgPC0gaHRtbF90ZXh0KHZub2RlcykKICAgIGNvdW50cyA8LSBhcy5udW1lcmljKGdzdWIoIltcXChcXCldIiwgIiIsIHZ0eHQpKQogICAgdmF0dHIgPC0gaHRtbF9hdHRyKHZub2RlcywgInN0eWxlIikKICAgIHBjdCA8LSBhcy5udW1lcmljKHN1YigiLio6KFtbOmRpZ2l0Ol1dKykuKiIsICJcXDEiLCB2YXR0cikpCiAgICBkYXRhLmZyYW1lKGNsYXNzID0gbGFicywgY291bnRzID0gY291bnRzLCBwY3QgPSBwY3QpCn0KCnBvbHMgPC0gIgpUcnVtcCwgZG9uYWxkLXRydW1wCkJhY2htYW5uLCBtaWNoZWxlLWJhY2htYW5uCkNydXosIHRlZC1jcnV6CkdpbmdyaWNoLCBuZXd0LWdpbmdyaWNoClBhbGluLCBzYXJhaC1wYWxpbgpTYW50b3J1bSwgcmljay1zYW50b3J1bQpXYWxrZXIsIHNjb3R0LXdhbGtlcgpQZXJyeSwgcmljay1wZXJyeQpSeWFuLCBwYXVsLXJ5YW4KTWNDYWluLCBqb2huLW1jY2FpbgpSdWJpbywgbWFyY28tcnViaW8KUm9tbmV5LCBtaXR0LXJvbW5leQpSYW5kIFBhdWwsIHJhbmQtcGF1bApDaHJpc3RpZSwgY2hyaXMtY2hyaXN0aWUKSGlsbGFyeSBDbGludG9uLCBoaWxsYXJ5LWNsaW50b24KT2JhbWEsIGJhcmFjay1vYmFtYQpLYXNpY2gsIGpvaG4ta2FzaWNoCkJpZGVuLCBqb2UtYmlkZW4KSmViIEJ1c2gsIGplYi1idXNoClNhbmRlcnMsIGJlcm5pZS1zCiIKCnBwIDwtIHJlYWQuY3N2KHRleHRDb25uZWN0aW9uKHBvbHMpLCBoZWFkID0gRkFMU0UsCiAgICAgICAgICAgICAgIHN0cmlwLndoaXRlID0gVFJVRSkKCnZjIDwtIHNhcHBseShwcFtbMl1dLCBmdW5jdGlvbihuKSB7IHByaW50KG4pOyBwb2xmYWMobil9W1syXV0pCnJvd25hbWVzKHZjKSA8LSBsYWJzCnZwIDwtIHNhcHBseShwcFtbMl1dLCBmdW5jdGlvbihuKSB7IHByaW50KG4pOyBwb2xmYWMobil9W1szXV0pCnJvd25hbWVzKHZwKSA8LSBsYWJzCgp2Y3AgPC0gcHJvcC50YWJsZSh0KHZjKSwgMSlbLCA2IDogMV0KCiMgY29sbmFtZXModmMpIDwtIHBwW1sxXV0KIyB3cml0ZS50YWJsZSh0KHZjKSwgZmlsZSA9ICJwb2xmYWMuZGF0IikKLS0+CgpJIHNjcmFwZWQgdGhlIGRhdGEgYXMgb2YgQXByaWwgMTEsIDIwMTcsIGZyb20gUE9MSVRJRkFDVDsgdGhleSBhcmUKYXZhaWxhYmxlIFtoZXJlXShodHRwczovL3N0YXQudWlvd2EuZWR1L35sdWtlL2RhdGEvcG9sZmFjLmRhdCkuCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CmlmICghIGZpbGUuZXhpc3RzKCJwb2xmYWMuZGF0IikpCiAgICBkb3dubG9hZC5maWxlKCJodHRwczovL3N0YXQudWlvd2EuZWR1L35sdWtlL2RhdGEvcG9sZmFjLmRhdCIsCiAgICAgICAgICAgICAgICAgICJwb2xmYWMuZGF0IikKcGZ0IDwtIHJlYWQudGFibGUoInBvbGZhYy5kYXQiKQp2Y3AgPC0gcHJvcC50YWJsZShhcy5tYXRyaXgocGZ0KSwgMSlbLCA2IDogMV0KY29sbmFtZXModmNwKSA8LSBnc3ViKCJcXC4iLCAiICIsIGNvbG5hbWVzKHZjcCkpCgpoZWFkKHZjcCkKCmBgYAoKVGhlIERhaWx5IEtvcyBjaGFydCBpcyBvcmRlcmVkIGJ5IHRoZSBwZXJjZW50YWdlIG9mIHN0YXRlbWVudHMgdGhhdAphcmUgbW9yZSBmYWxzZSB0aGFuIHRydWUuIEEgZnVuY3Rpb24gdG8gcHJvZHVjZSBhIGJhciBjaGFydCB3aXRoIGEKc3BlY2lmaWVkIGNvbG9yIHBhbGV0dGU6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CiMjIGxhdHRpY2UgdmVyc2lvbgpwb2xiYXJzIDwtIGZ1bmN0aW9uKGNvbCA9IGNtLmNvbG9ycyg2KSkgewogICAgYmFyY2hhcnQodmNwW29yZGVyKHJvd1N1bXModmNwWywgMSA6IDNdKSksIF0sIGF1dG8ua2V5ID0gVFJVRSwKICAgICAgICAgICAgIHBhci5zZXR0aW5ncyA9IGxpc3Qoc3VwZXJwb3NlLnBvbHlnb24gPSBsaXN0KGNvbCA9IGNvbCkpKQp9CgojIyBnZ3Bsb3QgdmVyc2lvbgoKZ3ZjcCA8LSBhcy5kYXRhLmZyYW1lKHZjcCkgfD4KICAgIHJvd25hbWVzX3RvX2NvbHVtbigiTmFtZSIpIHw+CiAgICBwaXZvdF9sb25nZXIoLTEsIG5hbWVzX3RvID0gIkdyYWRlIiwgdmFsdWVzX3RvID0gInByb3AiKSB8PgogICAgbXV0YXRlKEdyYWRlID0gZmN0X3JldihmY3RfaW5vcmRlcihHcmFkZSkpKQpubSA8LSBtdXRhdGUoZ3ZjcCwgR3JhZGUgPSBvcmRlcmVkKEdyYWRlKSkgfD4KICAgIGZpbHRlcihHcmFkZSA8PSAiSGFsZiBUcnVlIikgfD4KICAgIGdyb3VwX2J5KE5hbWUpIHw+CiAgICBzdW1tYXJpemUocHJvcCA9IHN1bShwcm9wKSkgfD4KICAgIGFycmFuZ2UoZGVzYyhwcm9wKSkgfD4KICAgIHB1bGwoTmFtZSkKZ3ZjcCA8LSBtdXRhdGUoZ3ZjcCwgTmFtZSA9IGZhY3RvcihOYW1lLCBubSkpCgpwdmNwIDwtIGdncGxvdChndmNwLCBhZXMoTmFtZSwgcHJvcCwgZmlsbCA9IEdyYWRlKSkgKwogICAgZ2VvbV9jb2wocG9zaXRpb24gPSAiZmlsbCIsIHdpZHRoID0gMC43KSArCiAgICBjb29yZF9mbGlwKCkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIsCiAgICAgICAgICBwbG90Lm1hcmdpbiA9IG1hcmdpbihyID0gNTApLAogICAgICAgICAgbGVnZW5kLnRleHQgPSBlbGVtZW50X3RleHQoc2l6ZSA9IDEwKSkgKwogICAgc2NhbGVfeV9jb250aW51b3VzKGxhYmVscyA9IHNjYWxlczo6cGVyY2VudCwgZXhwYW5kID0gYygwLCAwKSkgKwogICAgZ3VpZGVzKGZpbGwgPSBndWlkZV9sZWdlbmQodGl0bGUgPSBOVUxMLCBucm93ID0gMSwgcmV2ZXJzZSA9IFRSVUUpKSArCiAgICBsYWJzKHggPSAiIiwgeSA9ICIiKQoKcG9sYmFycyA8LSBmdW5jdGlvbihjb2wgPSBjbS5jb2xvcnMoNikpCiAgICBwdmNwICsgc2NhbGVfZmlsbF9tYW51YWwodmFsdWVzID0gcmV2KGNvbCkpCgpwb2xiYXJzKCkKYGBgCgpUaGUgb3JpZ2luYWwgRGFpbHkgS29zIGNoYXJ0IHNlZW1zIHRvIHVzZSBhIHNsaWdodGx5IG1vZGlmaWVkIHZlcnNpb24Kb2YgdGhlIENvbG9yIEJyZXdlciBgU3BlY3RyYWxgIHBhbGV0dGUsIGEgZGl2ZXJnaW5nIHBhbGV0dGUuCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnBvbGJhcnMoYnJld2VyLnBhbCg2LCAiU3BlY3RyYWwiKSkKZGtjb2xzIDwtIGJyZXdlci5wYWwoNiwgIlNwZWN0cmFsIikKZGtjb2xzWzRdIDwtICJsaWdodGdyZXkiCnBvbGJhcnMoZGtjb2xzKQpgYGAKClRoZSBKdW5rQ2hhcnRzIHBsb3QgdXNlcyBhbm90aGVyIGRpdmVyZ2luZyBwYWxldHRlLCBjbG9zZSB0byB0aGUKYEJsdWUtUmVkIGAgcGFsZXR0ZSBhdmFpbGFibGUgaW4gYGhjbHdpemFyZGAuCgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnJ3YmNvbHMgPC0gYygiIzRBNkZFMyIsICIjODU5NUUxIiwgIiNCNUJCRTMiLCAiI0UyRTJFMiIsCiAgICAgICAgICAgICAiI0U2QUZCOSIsICIjRTA3QjkxIiwgIiNEMzNGNkEiKQpwb2xiYXJzKHJ3YmNvbHMpCnBvbGJhcnMocmV2KHJ3YmNvbHMpKQpgYGAKCkFub3RoZXIgZGl2ZXJnaW5nIHBhbGV0dGU6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtaGlkZSJ9CnBvbGJhcnMoYnJld2VyLnBhbCg3LCAiUGlZRyIpKQpgYGAKCkEgc2VxdWVudGlhbCBwYWxldHRlOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwb2xiYXJzKHJldihicmV3ZXIucGFsKDYsICJPcmFuZ2VzIikpKQpgYGAKCjwhLS0KCnN1cHByZXNzV2FybmluZ3MocHJpbnQoCm1hcHBsb3Qocm93bmFtZXMoVVNDYW5jZXJSYXRlcykgfiBsb2cocmF0ZS5tYWxlKSArIGxvZyhyYXRlLmZlbWFsZSksCiAgICAgICAgZGF0YSA9IFVTQ2FuY2VyUmF0ZXMsCiAgICAgICAgbWFwID0gbWFwKCJjb3VudHkiLCBwbG90ID0gRkFMU0UsIGZpbGwgPSBUUlVFLAogICAgICAgICAgICAgICAgICBwcm9qZWN0aW9uID0gIm1lcmNhdG9yIikpCikpCnN1cHByZXNzV2FybmluZ3MocHJpbnQoCm1hcHBsb3Qocm93bmFtZXMoVVNDYW5jZXJSYXRlcykgfiBsb2cocmF0ZS5tYWxlKSArIGxvZyhyYXRlLmZlbWFsZSksCiAgICAgICAgZGF0YSA9IFVTQ2FuY2VyUmF0ZXMsCiAgICBjb2xyYW1wID0gY29sb3JSYW1wUGFsZXR0ZShicmV3ZXIucGFsKG4gPSA5LCBuYW1lID0gIlJlZHMiKSksCiAgICBib3JkZXIgPSBOQSwKICAgICAgICBtYXAgPSBtYXAoImNvdW50eSIsIHBsb3QgPSBGQUxTRSwgZmlsbCA9IFRSVUUsCiAgICAgICAgICAgICAgICAgIHByb2plY3Rpb24gPSAibWVyY2F0b3IiKSkKKSkKCmh0dHA6Ly9kYXRhLmxpYnJhcnkudmlyZ2luaWEuZWR1L3NldHRpbmctdXAtY29sb3ItcGFsZXR0ZXMtaW4tci8KaHR0cDovL3N0YXQ1NDUuY29tL2Jsb2NrMDE4X2NvbG9ycy5odG1sCgpodHRwczovL3lvdXR1LmJlL3ZKRzY5OFUyTXZvCgoKbGlicmFyeShnZ3Bsb3QyKQpnZ0hDTCA8LSBmdW5jdGlvbihMKSB7CnIgIDwtIHNlcSgwLDEsbGVuZ3RoPTIwMSkKdGggPC0gc2VxKDAsMipwaSwgbGVuZ3RoPTIwMSkKZCAgPC0gZXhwYW5kLmdyaWQocj1yLHRoPXRoKQpnZyA8LSB3aXRoKGQsZGF0YS5mcmFtZShkLHg9cipzaW4odGgpLHk9cipjb3ModGgpLAogICAgICAgICAgICAgICAgICAgICAgICB6PWhjbChoPTM2MCp0aC8oMipwaSksYz0xMDAqciwgbD1MKSkpCmdncGxvdChnZykgKwogIGdlb21fcG9pbnQoYWVzKHgseSwgY29sb3I9eiksIHNpemU9MykrCiAgc2NhbGVfY29sb3JfaWRlbnRpdHkoKStsYWJzKHg9IiIseT0iIikgKwogIGNvb3JkX2ZpeGVkKCkKCn0KCi0tPgoKCiMjIFJlYWRpbmcKClNlY3Rpb24gW19QZXJjZXB0aW9uIGFuZCBEYXRhClZpc3VhbGl6YXRpb25fXShodHRwczovL3NvY3Zpei5jby9sb29rYXRkYXRhLmh0bWwjcGVyY2VwdGlvbi1hbmQtZGF0YS12aXN1YWxpemF0aW9uKQppbiBbX0RhdGEgVmlzdWFsaXphdGlvbl9dKGh0dHBzOi8vc29jdml6LmNvLykuCgpDaGFwdGVyIFtfQ29sb3Igc2NhbGVzX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6L2NvbG9yLWJhc2ljcy5odG1sKQogIGluIFtfRnVuZGFtZW50YWxzIG9mIERhdGEKICBWaXN1YWxpemF0aW9uX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6LykuCgoKIyMgRXhlcmNpc2VzCgoxLiBBIGNvbG9yIGNhbiBiZSBzcGVjaWZpZWQgaW4gaGV4YWRlY2ltYWwgbm90YXRpb24uIEdpdmVuIHN1Y2ggYQogICAgY29sb3Igc3BlY2lmaWNhdGlvbiB5b3UgY2FuIGZpbmQgb3V0IHdoYXQgaXQgbG9va3MgbGlrZSBieSB1c2luZwogICAgaXQgaW4gYSBzaW1wbGUgcGxvdCwgb3IgYnkgdXNpbmcgdGhlIEdvb2dsZSBjb2xvciBwaWNrZXIuICBXaGljaAogICAgb2YgdGhlIGZvbGxvd2luZyBiZXN0IGRlc2NyaWJlIHRoZSBjb2xvciBgI0IyMjIyMmA/CgogICAgYS4gYSBzaGFkZSBvZiBncmVlbgogICAgYi4gYSBzaGFkZSBvZiBibHVlCiAgICBjLiBvcmFuZ2UKICAgIGQuIGEgc2hhZGUgb2YgcmVkCgoyLiBUaGUgZm9sbG93aW5nIHNob3dzIGhvdyB0byB2aWV3IHRoZSBjb2xvcnMgaW4gdGhlCiAgICBgUkNvbG9yQnJld2VyYCBwYWxldHRlIG5hbWVkIGBSZWRzYCB3aXRoIDcgY29sb3JzOgoKICAgIGBgYHtyLCBmaWcuY2FwID0gIiJ9CiAgICBsaWJyYXJ5KFJDb2xvckJyZXdlcikKICAgIGRpc3BsYXkuYnJld2VyLnBhbCg3LCAiUmVkcyIpCiAgICBgYGAKCiAgICBXaGljaCBvZiB0aGUgZm9sbG93aW5nIGBSQ29sb3JCcmV3ZXJgIHBhbGV0dGVzIGlzIGRpdmVyZ2luZz8KCiAgICBhLiBgQmx1ZXNgCiAgICBiLiBgUHVSZGAKICAgIGMuIGBTZXQxYAogICAgZC4gYFJkR3lgCg==
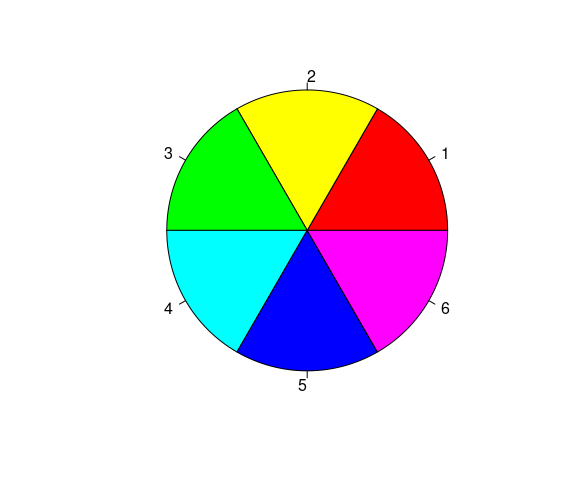
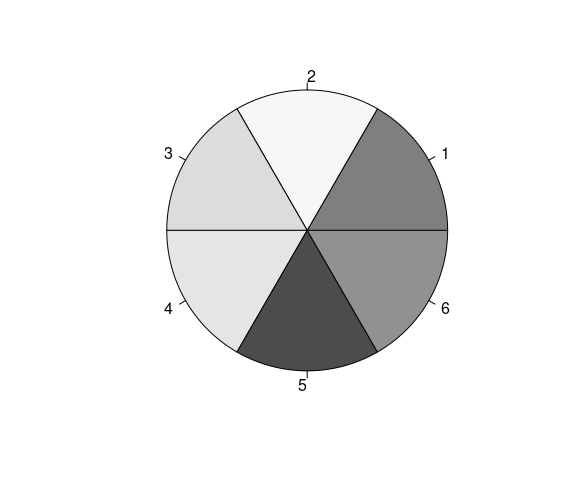

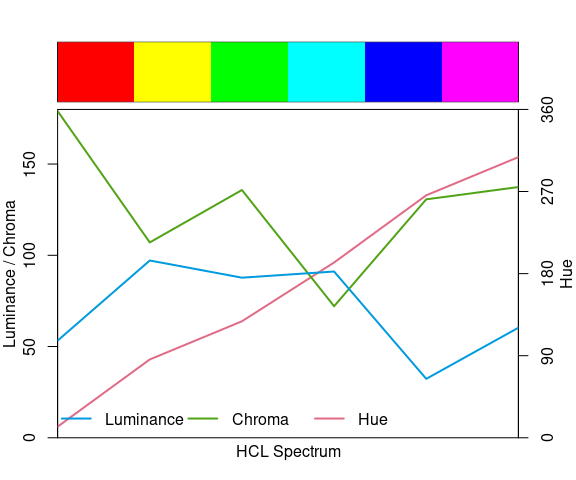

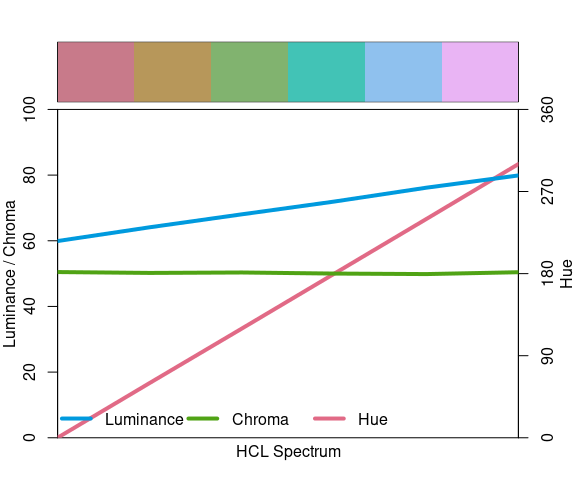
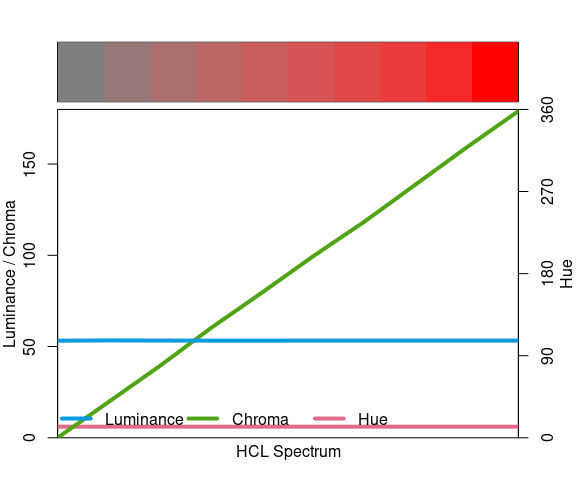
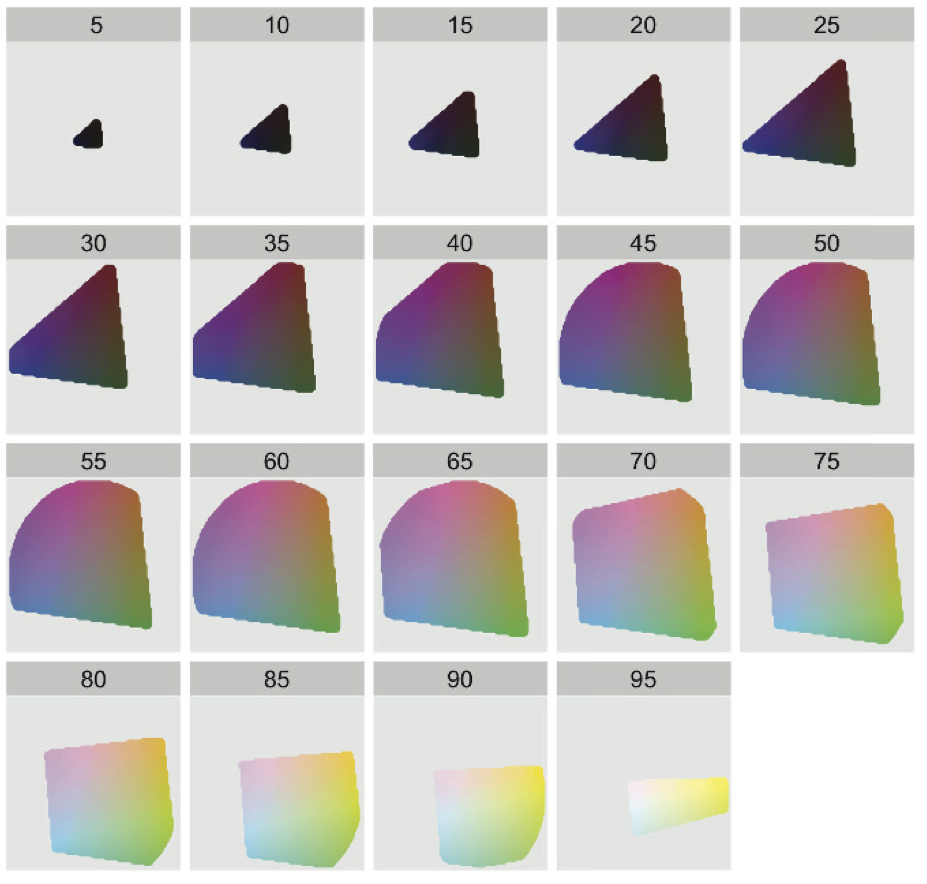
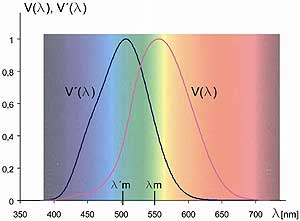


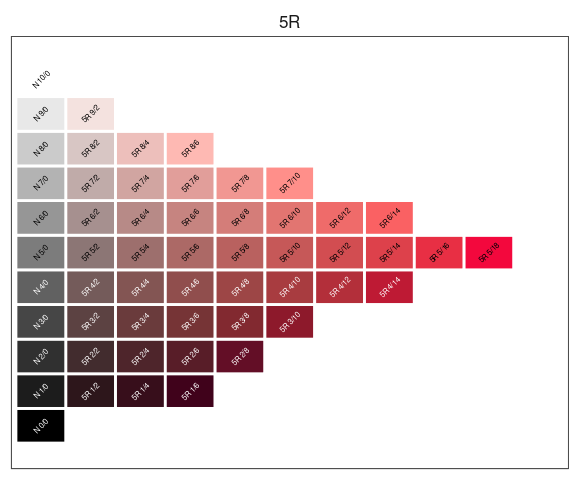
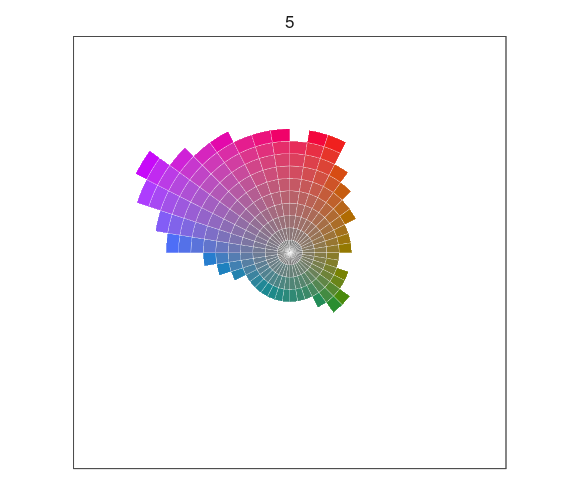
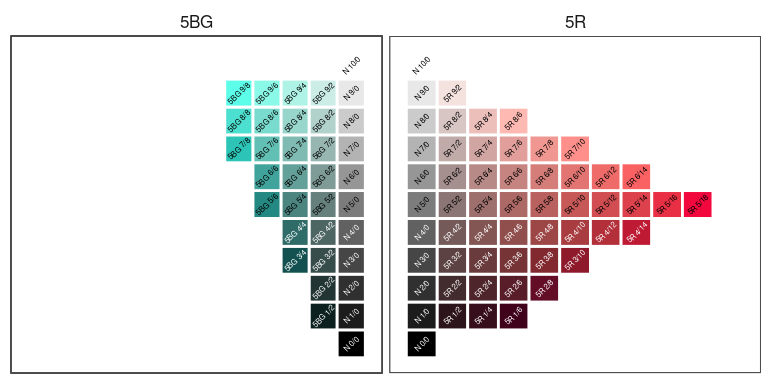
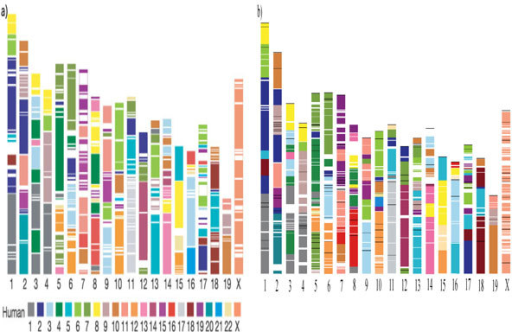

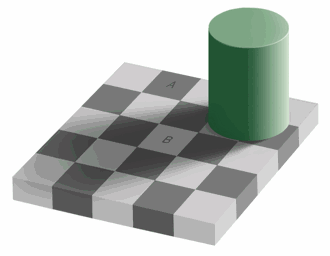



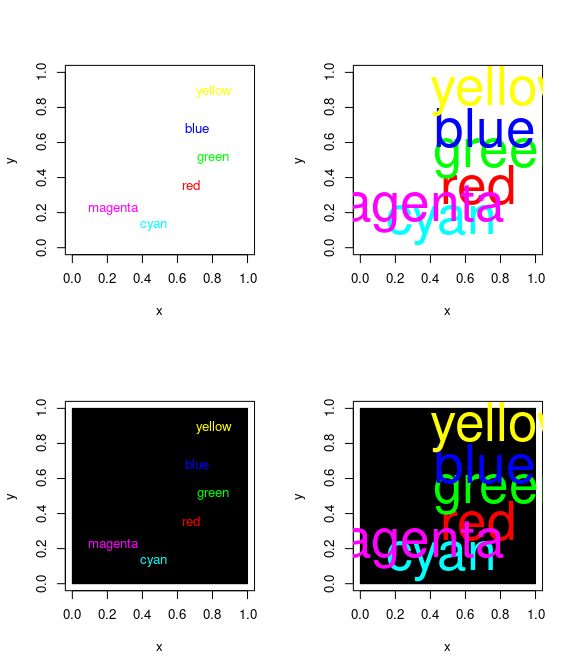





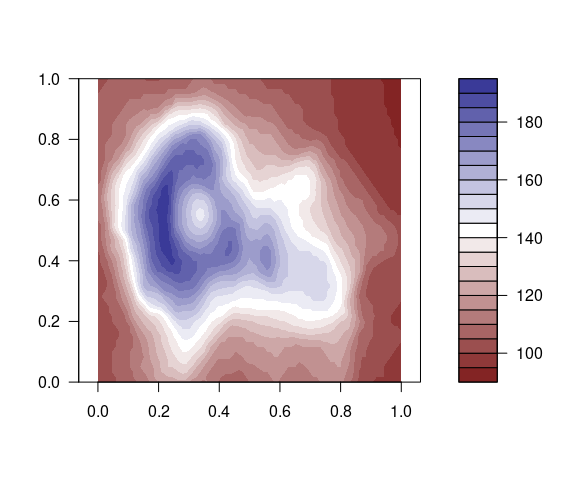
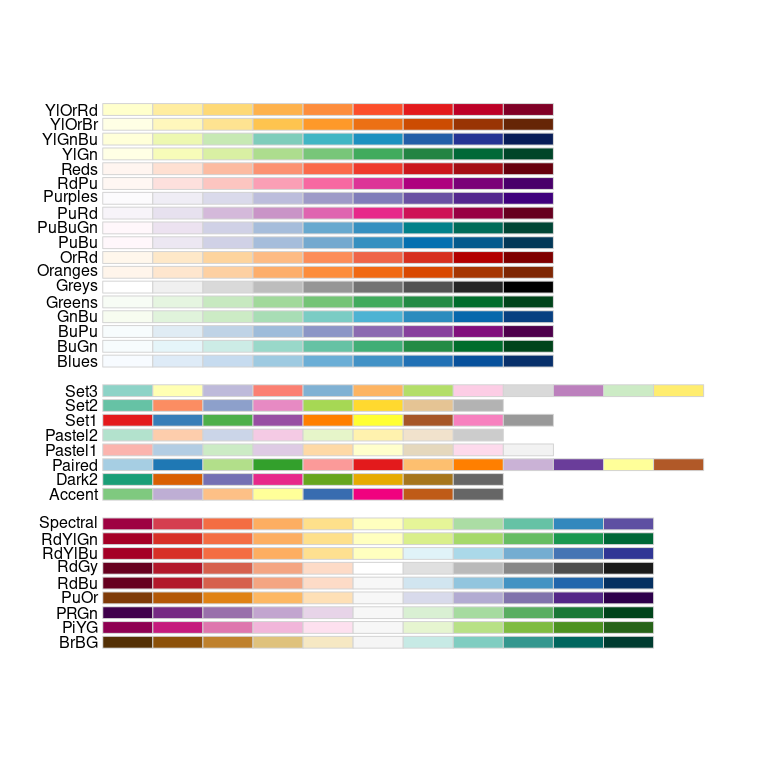




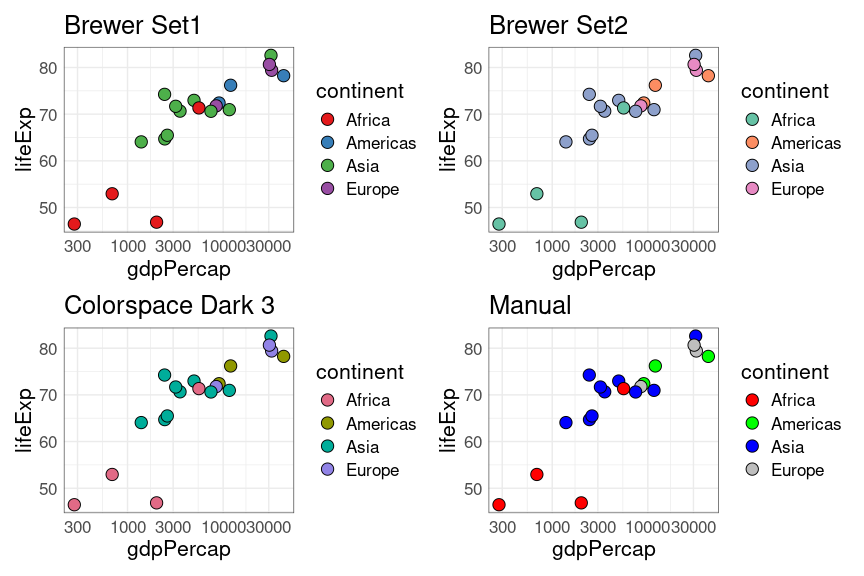

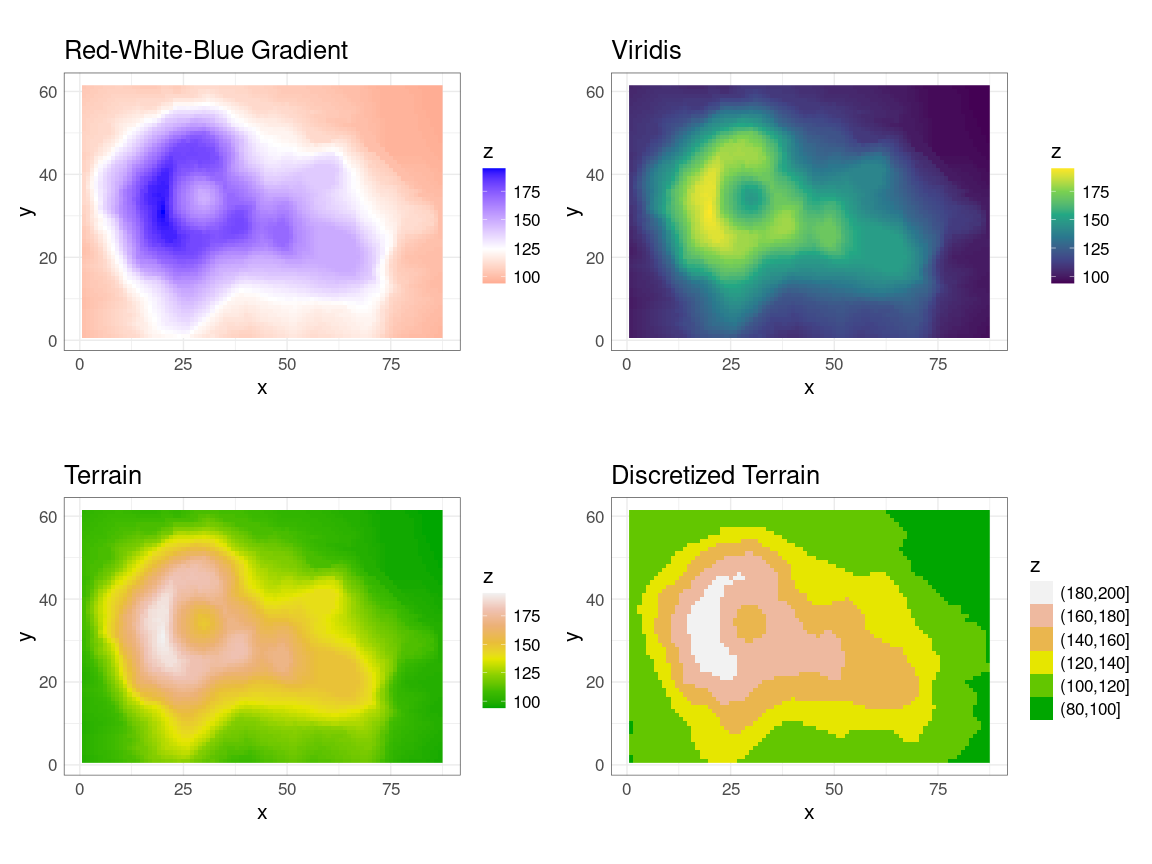
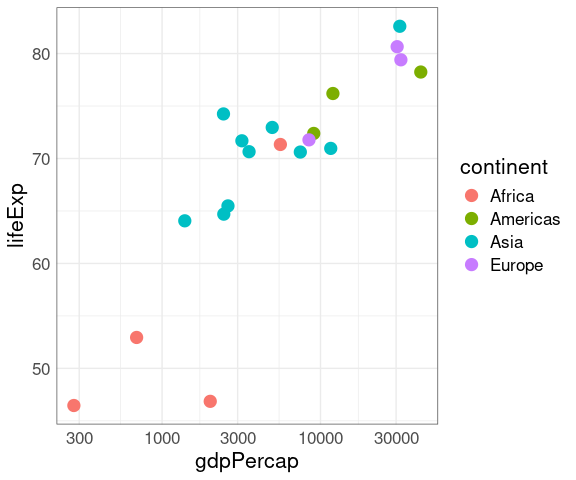
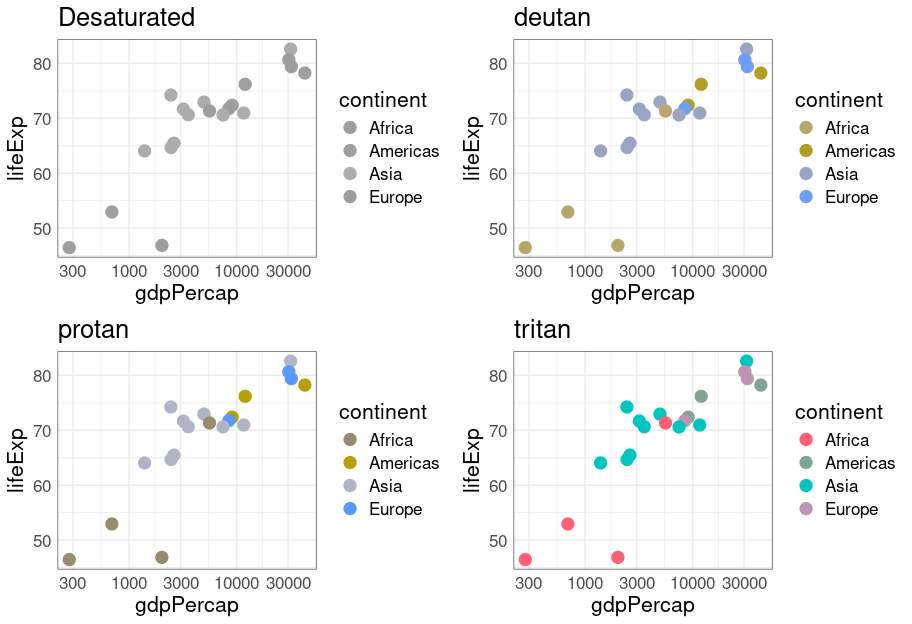

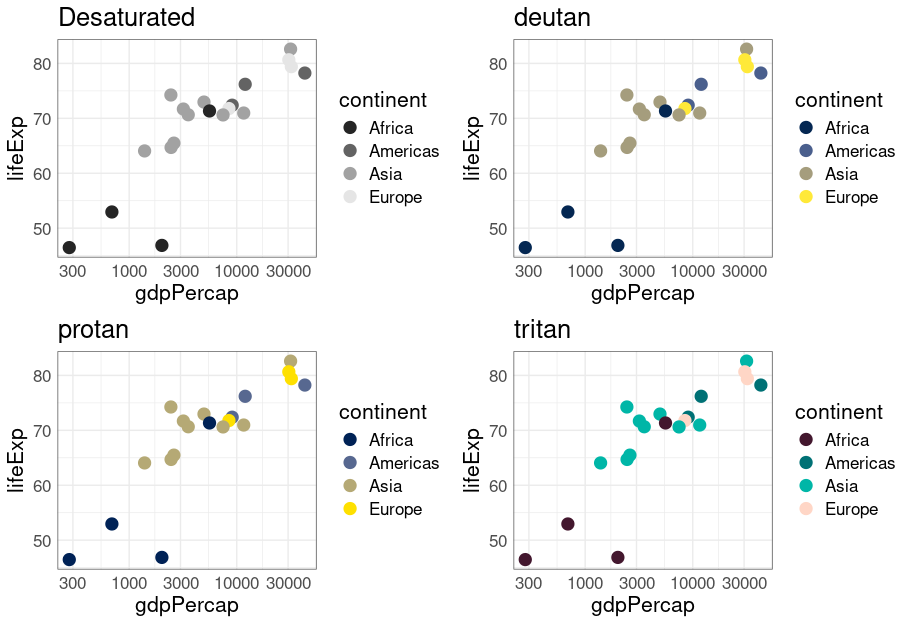


 Unless the viewer is very familiar with US geography.
Unless the viewer is very familiar with US geography.