University of Iowa

College of Liberal Arts and Sciences

• STAT:4580
• Syllabus
• Outline
• Homework
• Notes
• Resources
-->

Assignment 7 Notes

1. State Average Unemployment Rates

library(dplyr)
## 
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union
lausURL <- "http://www.stat.uiowa.edu/~luke/data/laus/laucntycur14-2018.txt"
lausFile <- "laucntycur14-2018.txt"
if (! file.exists(lausFile))
    download.file(lausURL, lausFile)
lausUS <- read.table(lausFile,
                     col.names = c("LAUSAreaCode", "State", "County",
                                   "Title", "Period",
                                   "LaborForce", "Employed",
                                   "Unemployed", "UnempRate"),
                     quote = "", sep = "|", skip = 6, strip.white = TRUE,
                     fill = TRUE)
footstart <- grep("------", lausUS$LAUSAreaCode)
lausUS <- lausUS[1 : (footstart - 1), ]
lausUS <- mutate(lausUS,
                 UnempRate = as.numeric(UnempRate),
                 LaborForce = as.numeric(gsub(",", "", LaborForce)),
                 Employed = as.numeric(gsub(",", "", Employed)),
                 Unemployed = as.numeric(gsub(",", "", Unemployed)))

After reading the data into a data frame lausUS the unemployment rate for each state can be computed as

\[ \frac{\text{number of unemployed in the state}}{\text{size of the labor force in the state}}. \]

• You can also compute this number as the weighted average of the county unemployment rates, weighted by the county labor force sizes.

• Simply averaging the unemployment rates produces the wrong state-level result: small counties receive much more weight than they should.

To see the difference we can compute both values:

unemp_by_state <- summarize(group_by(lausUS, State),
                            urate = 100 * sum(Unemployed) / sum(LaborForce),
                            urateNW = mean(UnempRate))

The map data is obtained with

gusa <- map_data("state")

To allow the map data to be merged with the unemployment data we can arrange that both data frames contain the state FIPS code in a variable named fips:

unemp_by_state <- rename(unemp_by_state, fips = State)
state.fips <-
    select(maps::state.fips, fips, region = polyname) |>
    mutate(region = sub(":.*", "", region)) |>
    unique()
gusa <- left_join(gusa, state.fips, "region")

A left join of the map and unemployment data is placed in gusa_unemp:

gusa_unemp <- left_join(gusa, unemp_by_state, "fips")

Since the unemployment rate is a continuous variable, a sequential palette is most appropriate. The default palette does not work well; the "Reds" palette from RColorBrewer is a good choice:

ggplot(gusa_unemp) +
    geom_polygon(aes(long, lat, group = group, fill = urate)) +
    coord_map() +
    scale_fill_distiller(palette = "Reds", direction = 1) +
    mapthm

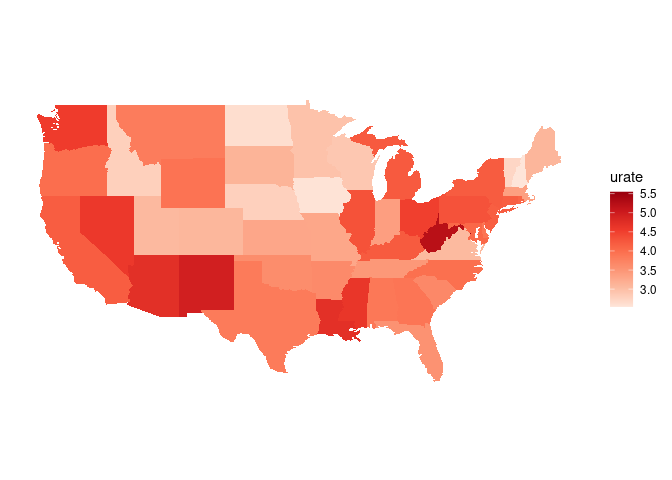
mapthm is a theme based on ggthemes::theme_map that keeps the guide on the right.

Using a faceted display we can look at the result for the incorrect unweighted computation of the state unemployment rate:

gusa_unemp_td <- gather(gusa_unemp, which, rate, urate, urateNW)
ggplot(gusa_unemp_td) +
    geom_polygon(aes(long, lat, group = group, fill = rate)) +
    coord_map() +
    scale_fill_distiller(palette = "Reds", direction = 1) +
    mapthm +
    facet_wrap(~ which, ncol = 1)

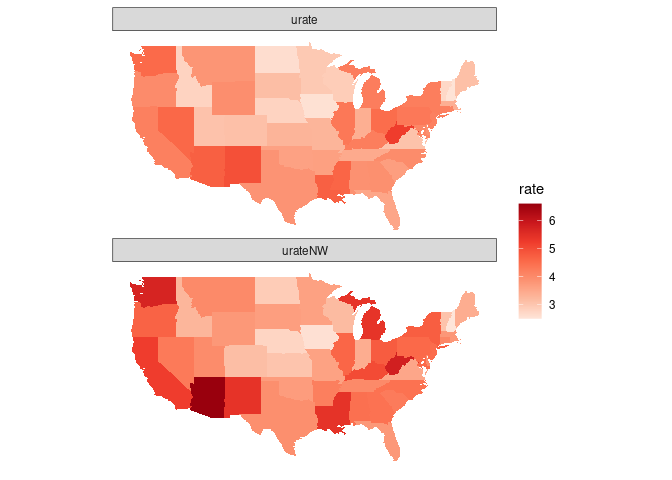
2. Iowa Monthly Unemployment Rates over Time

To create the four-month faceted plot it is useful to add county FIPS codes and to clean out the (p) from the final period.

lausUS <- mutate(lausUS,
                 Period = substr(Period, 1, 6),
                 fips = 1000 * State + County)

The map data with county FIPS codes:

fipstab <-
    transmute(maps::county.fips, fips, county = sub(":.*", "", polyname)) |>
    unique() |>
    separate(county, c("region", "subregion"), sep = ",")
giowa <- map_data("county", "iowa")
giowa <- left_join(giowa, fipstab, c("region", "subregion"))

A subset of the data for the four months to be shown and the variables needed:

periods <- paste(c("Mar", "Jun", "Sep", "Dec"), 18, sep = "-")
sublaus <- filter(lausUS, Period %in% periods)
sublaus <- select(sublaus, Period, UnempRate, fips)

Make the Period into an ordered factor with levels in the right order:

sublaus <- mutate(sublaus,
                  Period = factor(Period, ordered = TRUE, levels = periods))

Left join the map data with the unemployment data

giowa_laus <- left_join(giowa, sublaus, "fips")
## Warning in left_join(giowa, sublaus, "fips"): Detected an unexpected many-to-many relationship between `x` and `y`.
## ℹ Row 1 of `x` matches multiple rows in `y`.
## ℹ Row 789 of `y` matches multiple rows in `x`.
## ℹ If a many-to-many relationship is expected, set `relationship =
##   "many-to-many"` to silence this warning.

The faceted plot:

ggplot(giowa_laus) +
    geom_polygon(aes(long, lat, fill = UnempRate, group = group)) +
    coord_map() +
    scale_fill_distiller(palette = "Reds", direction = 1) +
    facet_wrap(~ Period) + mapthm

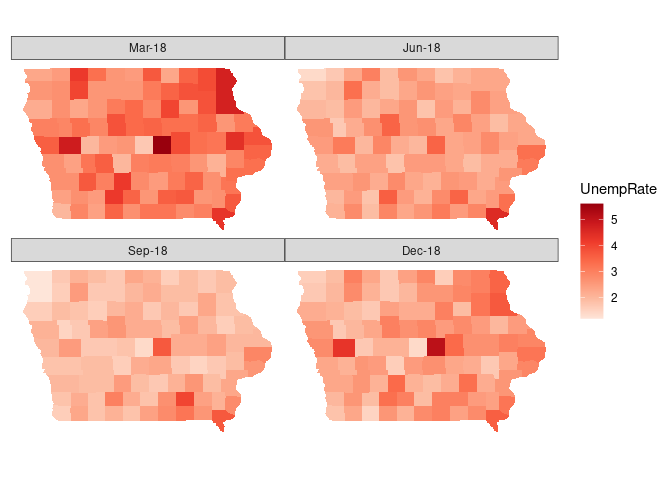
• A sequential palette is appropriate for the numeric unemployment rate.
• The limits argument to scale_fill_distiller could be used to make the scales in the state and county plots the same.

3. Comparison of Iowa Unemployment Rates

Create plot data with the differences as Udiff:

lausDec18 <- select(filter(lausUS, Period == "Dec-18"), fips, UnempRate)
lausDec17 <- select(filter(lausUS, Period == "Dec-17"), fips, UnempRate)

dlaus <- left_join(rename(lausDec18, U18 = UnempRate),
                   rename(lausDec17, U17 = UnempRate),
                   "fips")
dlaus <- mutate(dlaus, Udiff = U18 - U17)

giowa_dlaus <- left_join(giowa, dlaus, "fips")

A diverging color scheme is most appropriate for a comparison.

• When using a diverging scheme it is important to match the neutral data value, zero in this case, with the neutral color.

• The ssale_fill_gratient2 function makes this easy.

• For other continuous scales you can use the limits or the rescaler arguments.

• For a discrete scale you should make sure to place the neutral value in the middle of the neutral color bin.

A map using scale_fill_gratient2:

p <- ggplot(giowa_dlaus) +
    geom_polygon(aes(long, lat, fill = Udiff, group = group)) +
    coord_map() + mapthm
p + scale_fill_gradient2()

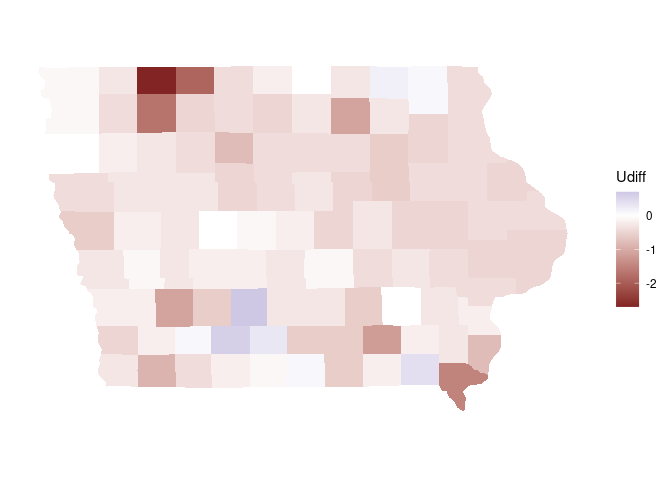
To use the same hues with red mapped to the high value you can use the muted function from the scales package:

library(scales)
p + scale_fill_gradient2(low = muted("blue"), high = muted("red"))

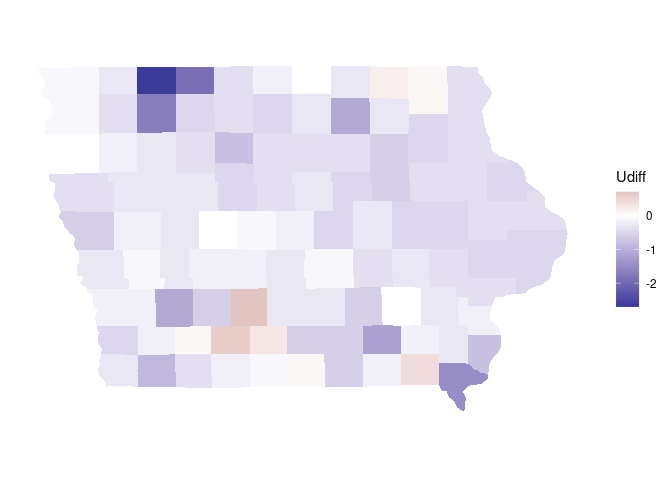
Using "RdBu" from RColorBrewer without adjustment places the neutral zero value in the wrong place:

p + scale_fill_distiller(palette = "RdBu")

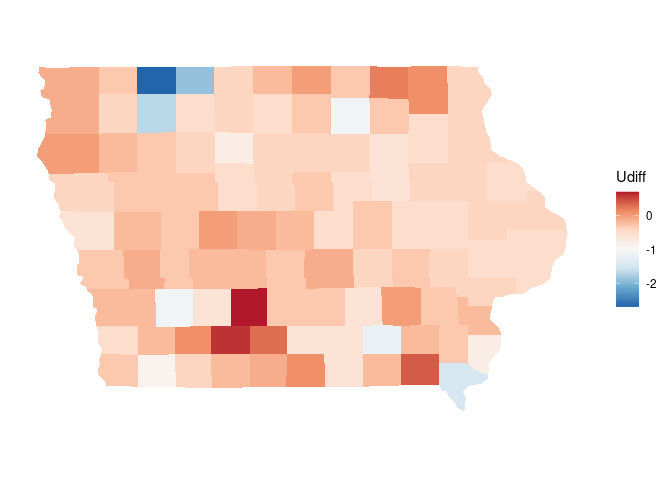
Using the limits argument is one way to address this:

lim <- max(abs(range(giowa_dlaus$Udiff)))
p + scale_fill_distiller(palette = "RdBu", limits = c(-lim, lim))

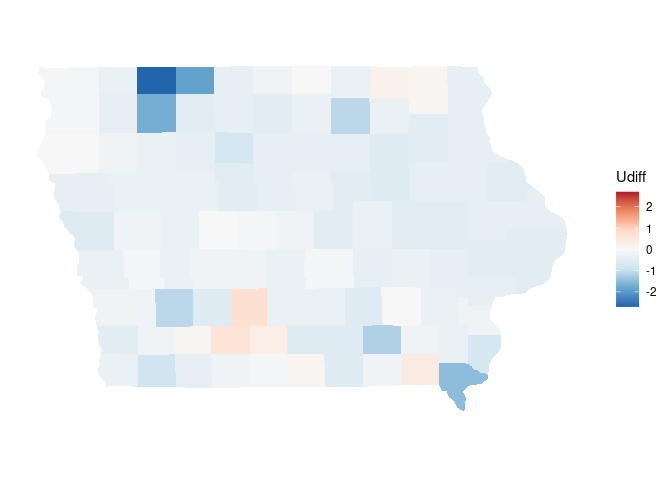
An alternative is to provide a rescaler function:

rscl <- function(x, from) 0.5 + 0.495 * x / max(abs(from))
p + scale_fill_distiller(palette = "RdBu", rescaler = rscl)

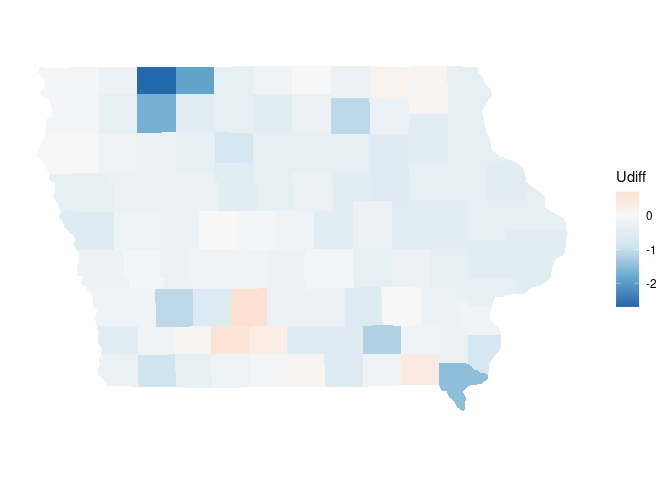
For a discretized scale, use breaks that include the neutral value zero in the middle of the middle interval and make sure the mapping uses all the classes to keep the neutral color on the middle interval:

breaks <- seq(-2.25, 2.25, len = 10)
breaks
##  [1] -2.25 -1.75 -1.25 -0.75 -0.25  0.25  0.75  1.25  1.75  2.25

pd <- ggplot(giowa_dlaus) +
    geom_polygon(aes(long, lat, fill = cut(Udiff, breaks), group = group)) +
    coord_map() + mapthm
pd + scale_fill_brewer(palette = "RdBu", direction = -1, drop = FALSE)

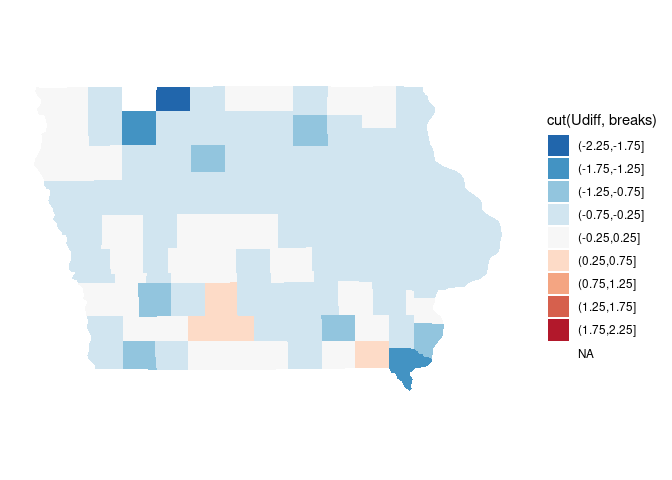
It would be possible to drop the classes not represented on the map from the legend.

4. Optional: Animated Maps over Time

One possible approach is available here

This work is licensed under the CC BY-NC 3.0 Creative Commons License.