1. Abrasion Loss in Rubber Samples
library(lattice)
library(ggplot2)
library(dplyr)
theme_set(theme_minimal() +
theme(text = element_text(size = 16)) +
theme(panel.border = element_rect(color = "grey30", fill = NA)))
if (! file.exists("abrasion.csv"))
download.file("http://www.stat.uiowa.edu/~luke/data/abrasion.csv",
"abrasion.csv")
abrasion <- read.csv("abrasion.csv")
A scatterplot matrix of the three variables:
splom(abrasion)
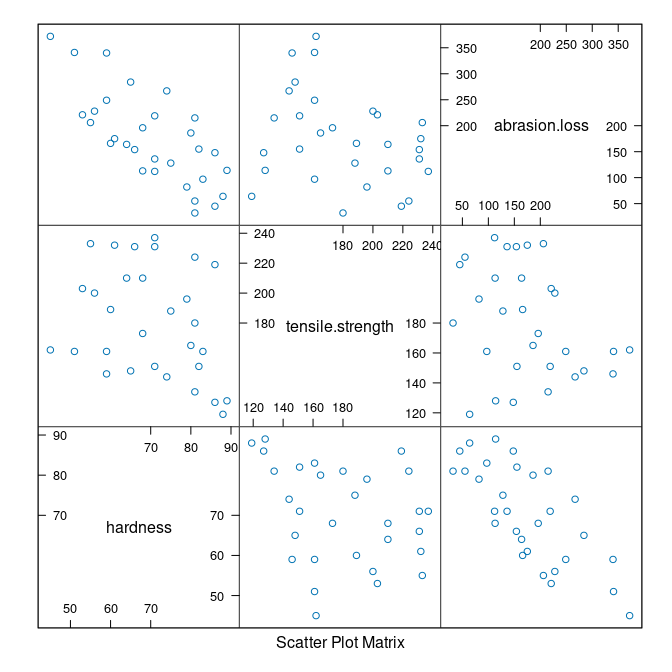
The plot of abrasion loss against hardness shows a weak decreasing relationship.
A coplot can be used to explore the joint relationship:
abrasion_hgroup <- mutate(abrasion, hgroup = cut_number(hardness, 4))
ggplot(abrasion_hgroup, aes(tensile.strength, abrasion.loss)) +
geom_point() +
facet_wrap(~ hgroup)
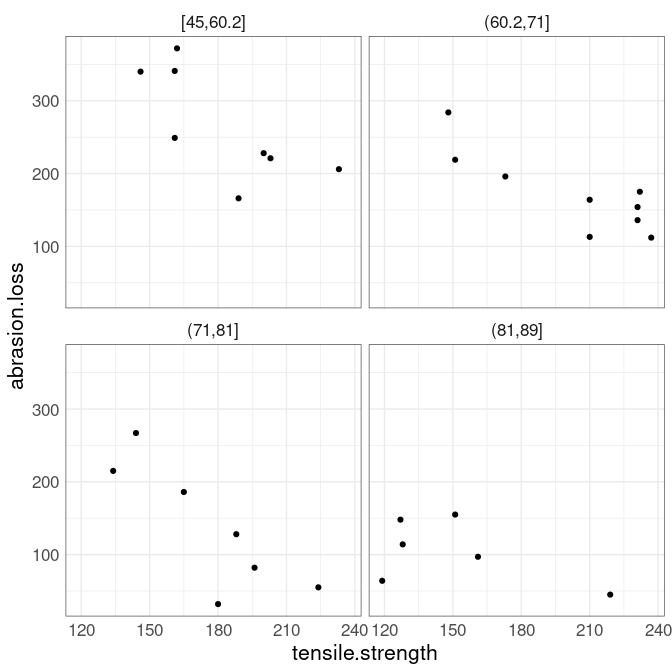
At each level of hardness, abrasion loss decreases as tensile strength increases.
Showing a muted version of the full data in the background provides context for comparing the facets:
ggplot(abrasion_hgroup, aes(tensile.strength, abrasion.loss)) +
geom_point(data = abrasion, color = "grey") +
geom_point(size = 2) +
facet_wrap(~ hgroup)
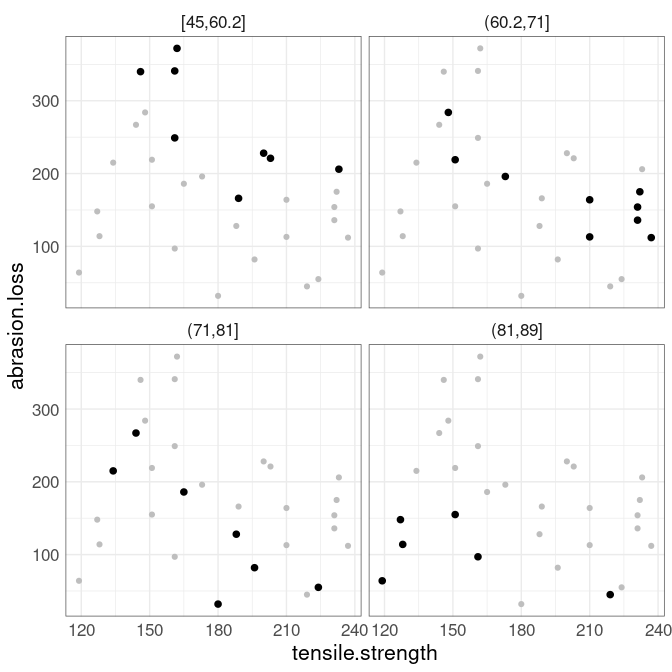
As hardness increases, the abrasion loss/tensile strength relation moves lower.
2. Arrival and Departure Delays
Start by taking a 10% sample to make creating useful scatterplots easier:
library(nycflights13)
fl_30K <- sample_frac(flights, 0.1)
A plot of the full data shows that the bulk of flights have short arrival and departure delays. For those with longer delays, the arrival and departure delays are close to the same. This can be made easier to see by adding a 45 degree line:
ggplot(fl_30K, aes(dep_delay, arr_delay)) +
geom_point(size = 0.5) +
geom_abline(intercept = 0, slope = 1, color = "red") # not really needed
## Warning: Removed 938 rows containing missing values or values outside the scale range
## (`geom_point()`).
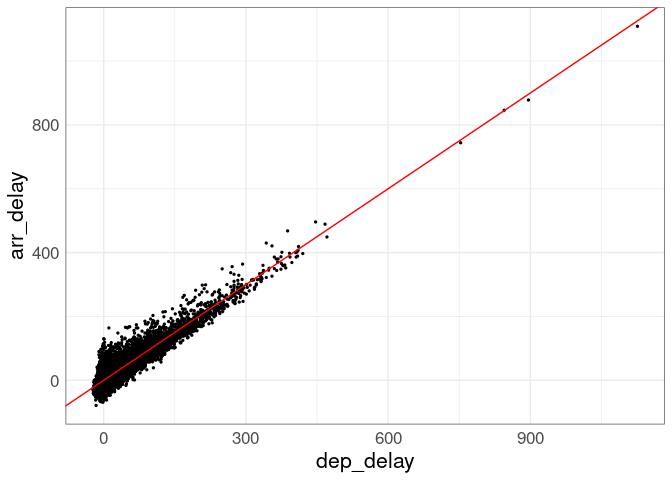
About 85% of the sample with non-missing departure delays had departure delays of at most 30 minutes.
Since delays are only reported to the nearest minute and the data set is still large there is a lot of heaping on the integer values, in particular for the departure delays. Alpha blending helps some, but adding jitter in the horizontal direction is also helpful.
p <- ggplot(filter(fl_30K, dep_delay <= 30),
aes(dep_delay, arr_delay)) +
geom_point(size = 0.5, alpha = 0.05, na.rm = TRUE,
position = position_jitter(height = 0, width = 0.5))
p
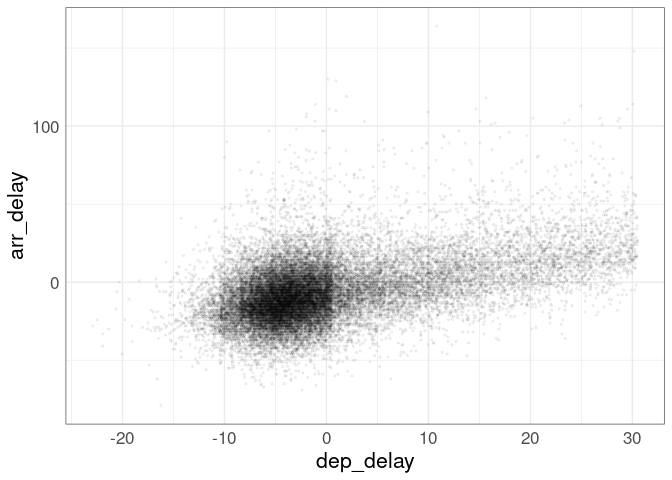
At the right alpha level a step down at zero is visible. A histogram of the departure delays in the a five minute interval of zero suggests that there might be some generous rounding down for flights with a one minute delay:
ggplot(filter(fl_30K, dep_delay <= 5, dep_delay > -5), aes(dep_delay)) +
geom_histogram(binwidth = 1, fill = "grey", color = "black")
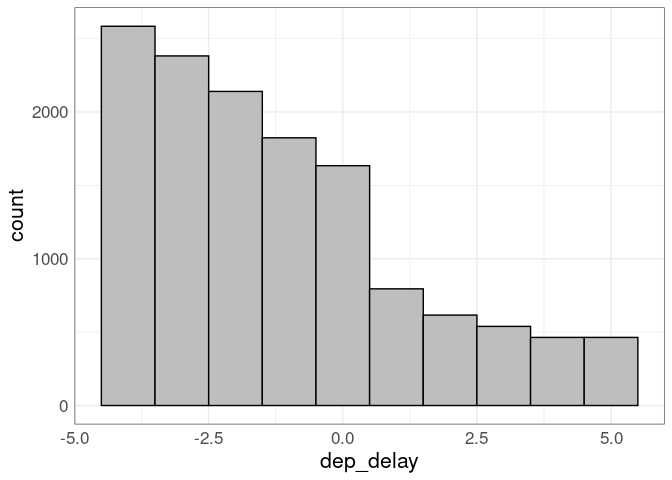
There is still a lot of over-plotting, even with the reduced sample. Adding density estimates can help make the distribution of the delay times easier to see.
p1 <- p + geom_density2d(bins = 6, color = "red", na.rm = TRUE)
ggExtra::ggMarginal(p1)
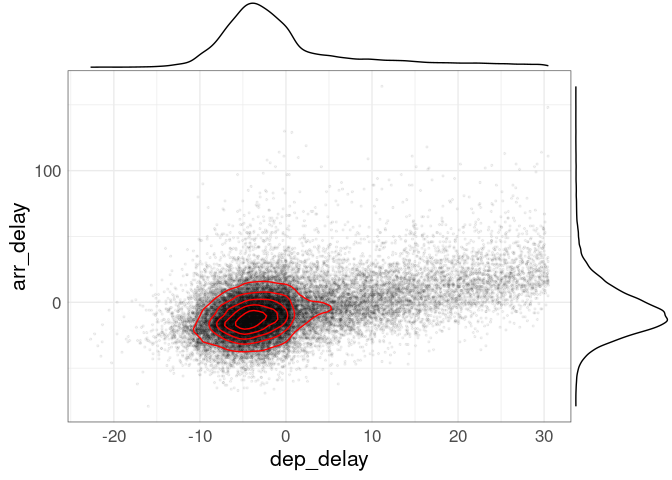
The additions show that most departures and arrivals are not delayed, and that for the flights departing close to on time there is very little relationship between the arrival and departure times; they seem to be nearly independent.
Both the marginal density estimate for the departure delays and the joint density estimates suggest some slightly unusual behavior at the zero point.
3. Wind Speed, Time of Day, and Departure Delays
Join the weather data to the flights data using origin and time_hour as the key. Bring in only the variables we need:
fl <- left_join(flights, select(weather, origin, time_hour, wind_speed),
c("origin", "time_hour"))
Check that this key is a good primary key for the weather table:
nrow(filter(count(weather, origin, time_hour), n > 1))
## [1] 0
(! anyNA(weather$origin)) & (! anyNA(weather$time_hour))
## [1] TRUE
Include only summer months, and drop rows with missing values or where the wind speed is above 30 mph:
library(tidyr)
fls <- filter(fl, month %in% 6:8) |>
drop_na() |>
filter(wind_speed <= 30)
A plot of the proportion of departures that are delayed at each wind speed:
group_by(fls, wind_speed) |>
summarize(p_delay = mean(dep_delay > 0), n = n()) |>
ungroup() |>
ggplot(aes(wind_speed, p_delay)) +
geom_point() +
geom_smooth(aes(weight = n))
## `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
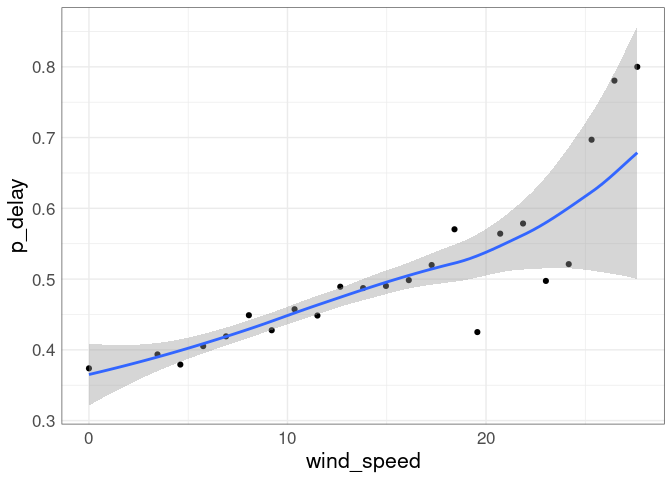
There appears to be an increase in the proportion of delayed departures associated with an increase in wind speed.
However, a coplot of the proportion of delayed departures against departure hour conditioned on wind speed shows that there is also a positive association with the departure hour, and that association does not vary much with wind speed:
group_by(fls, wind_speed, hour) |>
summarize(p_delay = mean(dep_delay > 0), n = n()) |>
ungroup() |>
ggplot(aes(hour, p_delay)) +
geom_point() +
geom_smooth(aes(weight = n)) +
facet_wrap(~ cut_number(wind_speed, 6))
## `summarise()` has grouped output by 'wind_speed'. You can override using the
## `.groups` argument.
## `geom_smooth()` using method = 'loess' and formula = 'y ~ x'
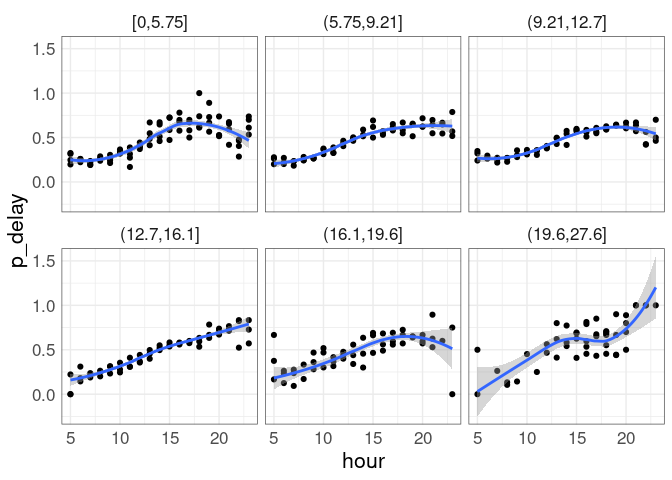
A reason may be that wind speed increases throughout the day until around 5 PM (17:00 hours):
ggplot(fls, aes(hour, wind_speed)) + geom_smooth()
## `geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'
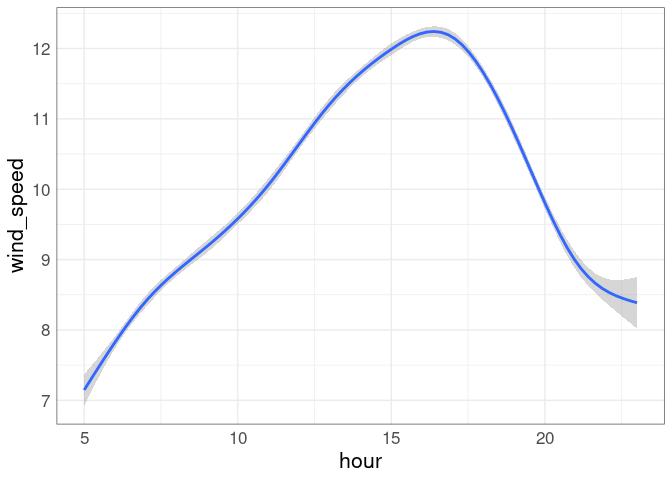
The coplot shows that the proportion of delayed departures increases roughly linearly until around 5 PM for all wind speed ranges. A linear regression of the proportion of delayed departures against hour and wind_speed for departures prior to 5 PM shows a very small coefficient for wind speed once time of day is accounted for:
fls_prop <- group_by(fls, wind_speed, hour) |>
summarize(p_delay = mean(dep_delay > 0), n = n()) |>
ungroup() |>
filter(hour <= 17)
## `summarise()` has grouped output by 'wind_speed'. You can override using the
## `.groups` argument.
lm(p_delay ~ hour + wind_speed, weights = n, data = fls_prop)
##
## Call:
## lm(formula = p_delay ~ hour + wind_speed, data = fls_prop, weights = n)
##
## Coefficients:
## (Intercept) hour wind_speed
## -0.0259521 0.0379807 -0.0002924
LS0tCnRpdGxlOiAiQXNzaWdubWVudCA4IE5vdGVzIgpvdXRwdXQ6CiAgaHRtbF9kb2N1bWVudDoKICAgIHRvYzogeWVzCiAgICBjb2RlX2Rvd25sb2FkOiB0cnVlCiAgICBjb2RlX2ZvbGRpbmc6ICJoaWRlIgotLS0KCmBgYHtyIGdsb2JhbF9vcHRpb25zLCBpbmNsdWRlID0gRkFMU0V9CmtuaXRyOjpvcHRzX2NodW5rJHNldChjb2xsYXBzZSA9IFRSVUUpCmBgYAoKIyMgMS4gQWJyYXNpb24gTG9zcyBpbiBSdWJiZXIgU2FtcGxlcwoKYGBge3IsIG1lc3NhZ2UgPSBGQUxTRX0KbGlicmFyeShsYXR0aWNlKQpsaWJyYXJ5KGdncGxvdDIpCmxpYnJhcnkoZHBseXIpCnRoZW1lX3NldCh0aGVtZV9taW5pbWFsKCkgKwogICAgICAgICAgdGhlbWUodGV4dCA9IGVsZW1lbnRfdGV4dChzaXplID0gMTYpKSArCiAgICAgICAgICB0aGVtZShwYW5lbC5ib3JkZXIgPSBlbGVtZW50X3JlY3QoY29sb3IgPSAiZ3JleTMwIiwgZmlsbCA9IE5BKSkpCmlmICghIGZpbGUuZXhpc3RzKCJhYnJhc2lvbi5jc3YiKSkKICAgIGRvd25sb2FkLmZpbGUoImh0dHA6Ly93d3cuc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9hYnJhc2lvbi5jc3YiLAogICAgICAgICAgICAgICAgICAiYWJyYXNpb24uY3N2IikKYWJyYXNpb24gPC0gcmVhZC5jc3YoImFicmFzaW9uLmNzdiIpCmBgYAoKQSBzY2F0dGVycGxvdCBtYXRyaXggb2YgdGhlIHRocmVlIHZhcmlhYmxlczoKCmBgYHtyLCBmaWcud2lkdGggPSA3LCBmaWcuaGVpZ2h0ID0gN30Kc3Bsb20oYWJyYXNpb24pCmBgYAoKVGhlIHBsb3Qgb2YgYWJyYXNpb24gbG9zcyBhZ2FpbnN0IGhhcmRuZXNzIHNob3dzIGEgd2VhayBkZWNyZWFzaW5nCnJlbGF0aW9uc2hpcC4KCkEgY29wbG90IGNhbiBiZSB1c2VkIHRvIGV4cGxvcmUgdGhlIGpvaW50IHJlbGF0aW9uc2hpcDoKCmBgYHtyLCBmaWcud2lkdGggPSA3LCBmaWcuaGVpZ2h0ID0gN30KYWJyYXNpb25faGdyb3VwIDwtIG11dGF0ZShhYnJhc2lvbiwgaGdyb3VwID0gY3V0X251bWJlcihoYXJkbmVzcywgNCkpCmdncGxvdChhYnJhc2lvbl9oZ3JvdXAsIGFlcyh0ZW5zaWxlLnN0cmVuZ3RoLCBhYnJhc2lvbi5sb3NzKSkgKwogICAgZ2VvbV9wb2ludCgpICsKICAgIGZhY2V0X3dyYXAofiBoZ3JvdXApCmBgYAoKQXQgZWFjaCBsZXZlbCBvZiBoYXJkbmVzcywgYWJyYXNpb24gbG9zcyBkZWNyZWFzZXMgYXMgdGVuc2lsZSBzdHJlbmd0aAppbmNyZWFzZXMuCgpTaG93aW5nIGEgbXV0ZWQgdmVyc2lvbiBvZiB0aGUgZnVsbCBkYXRhIGluIHRoZSBiYWNrZ3JvdW5kIHByb3ZpZGVzCmNvbnRleHQgZm9yIGNvbXBhcmluZyB0aGUgZmFjZXRzOgoKYGBge3IsIGZpZy53aWR0aCA9IDcsIGZpZy5oZWlnaHQgPSA3fQpnZ3Bsb3QoYWJyYXNpb25faGdyb3VwLCBhZXModGVuc2lsZS5zdHJlbmd0aCwgYWJyYXNpb24ubG9zcykpICsKICAgIGdlb21fcG9pbnQoZGF0YSA9IGFicmFzaW9uLCBjb2xvciA9ICJncmV5IikgKwogICAgZ2VvbV9wb2ludChzaXplID0gMikgKwogICAgZmFjZXRfd3JhcCh+IGhncm91cCkKYGBgCgpBcyBoYXJkbmVzcyBpbmNyZWFzZXMsIHRoZSBhYnJhc2lvbiBsb3NzL3RlbnNpbGUgc3RyZW5ndGggcmVsYXRpb24KbW92ZXMgbG93ZXIuCgoKIyMgMi4gQXJyaXZhbCBhbmQgRGVwYXJ0dXJlIERlbGF5cwoKU3RhcnQgYnkgdGFraW5nIGEgMTAlIHNhbXBsZSB0byBtYWtlIGNyZWF0aW5nIHVzZWZ1bCBzY2F0dGVycGxvdHMgZWFzaWVyOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLXNob3cifQpsaWJyYXJ5KG55Y2ZsaWdodHMxMykKZmxfMzBLIDwtIHNhbXBsZV9mcmFjKGZsaWdodHMsIDAuMSkKYGBgCgpBIHBsb3Qgb2YgdGhlIGZ1bGwgZGF0YSBzaG93cyB0aGF0IHRoZSBidWxrIG9mIGZsaWdodHMgaGF2ZSBzaG9ydAphcnJpdmFsIGFuZCBkZXBhcnR1cmUgZGVsYXlzLiBGb3IgdGhvc2Ugd2l0aCBsb25nZXIgZGVsYXlzLCB0aGUKYXJyaXZhbCBhbmQgZGVwYXJ0dXJlIGRlbGF5cyBhcmUgY2xvc2UgdG8gdGhlIHNhbWUuIFRoaXMgY2FuIGJlIG1hZGUKZWFzaWVyIHRvIHNlZSBieSBhZGRpbmcgYSA0NSBkZWdyZWUgbGluZToKICAKYGBge3J9CmdncGxvdChmbF8zMEssIGFlcyhkZXBfZGVsYXksIGFycl9kZWxheSkpICsKICAgIGdlb21fcG9pbnQoc2l6ZSA9IDAuNSkgKwogICAgZ2VvbV9hYmxpbmUoaW50ZXJjZXB0ID0gMCwgc2xvcGUgPSAxLCBjb2xvciA9ICJyZWQiKSAjIG5vdCByZWFsbHkgbmVlZGVkCmBgYAoKQWJvdXQKYHIgcm91bmQoMTAwICogbWVhbihmbF8zMEskZGVwX2RlbGF5IDw9IDMwLCBuYS5ybSA9IFRSVUUpKWAlCm9mIHRoZSBzYW1wbGUgd2l0aCBub24tbWlzc2luZyBkZXBhcnR1cmUgZGVsYXlzIGhhZCBkZXBhcnR1cmUgZGVsYXlzCm9mIGF0IG1vc3QgMzAgbWludXRlcy4KClNpbmNlIGRlbGF5cyBhcmUgb25seSByZXBvcnRlZCB0byB0aGUgbmVhcmVzdCBtaW51dGUgYW5kIHRoZSBkYXRhIHNldAppcyBzdGlsbCBsYXJnZSB0aGVyZSBpcyBhIGxvdCBvZiBoZWFwaW5nIG9uIHRoZSBpbnRlZ2VyIHZhbHVlcywgaW4KcGFydGljdWxhciBmb3IgdGhlIGRlcGFydHVyZSBkZWxheXMuIEFscGhhIGJsZW5kaW5nIGhlbHBzIHNvbWUsIGJ1dAphZGRpbmcgaml0dGVyIGluIHRoZSBob3Jpem9udGFsIGRpcmVjdGlvbiBpcyBhbHNvIGhlbHBmdWwuCgpgYGB7cn0KcCA8LSBnZ3Bsb3QoZmlsdGVyKGZsXzMwSywgZGVwX2RlbGF5IDw9IDMwKSwKICAgICAgICAgICAgYWVzKGRlcF9kZWxheSwgYXJyX2RlbGF5KSkgKwogICAgZ2VvbV9wb2ludChzaXplID0gMC41LCBhbHBoYSA9IDAuMDUsIG5hLnJtID0gVFJVRSwKICAgICAgICAgICAgICAgcG9zaXRpb24gPSBwb3NpdGlvbl9qaXR0ZXIoaGVpZ2h0ID0gMCwgd2lkdGggPSAwLjUpKQpwCmBgYAoKQXQgdGhlIHJpZ2h0IGFscGhhIGxldmVsIGEgc3RlcCBkb3duIGF0IHplcm8gaXMgdmlzaWJsZS4gQSBoaXN0b2dyYW0Kb2YgdGhlIGRlcGFydHVyZSBkZWxheXMgaW4gdGhlIGEgZml2ZSBtaW51dGUgaW50ZXJ2YWwgb2YgemVybyBzdWdnZXN0cwp0aGF0IHRoZXJlIG1pZ2h0IGJlIHNvbWUgZ2VuZXJvdXMgcm91bmRpbmcgZG93biBmb3IgZmxpZ2h0cyB3aXRoIGEgb25lCm1pbnV0ZSBkZWxheToKCmBgYHtyfQpnZ3Bsb3QoZmlsdGVyKGZsXzMwSywgZGVwX2RlbGF5IDw9IDUsIGRlcF9kZWxheSA+IC01KSwgYWVzKGRlcF9kZWxheSkpICsKICAgIGdlb21faGlzdG9ncmFtKGJpbndpZHRoID0gMSwgZmlsbCA9ICJncmV5IiwgY29sb3IgPSAiYmxhY2siKQpgYGAKClRoZXJlIGlzIHN0aWxsIGEgbG90IG9mIG92ZXItcGxvdHRpbmcsIGV2ZW4gd2l0aCB0aGUgcmVkdWNlZCBzYW1wbGUuCkFkZGluZyBkZW5zaXR5IGVzdGltYXRlcyBjYW4gaGVscCBtYWtlIHRoZSBkaXN0cmlidXRpb24gb2YgdGhlIGRlbGF5CnRpbWVzIGVhc2llciB0byBzZWUuCgpgYGB7cn0KcDEgPC0gcCArIGdlb21fZGVuc2l0eTJkKGJpbnMgPSA2LCBjb2xvciA9ICJyZWQiLCBuYS5ybSA9IFRSVUUpCmdnRXh0cmE6OmdnTWFyZ2luYWwocDEpCmBgYAoKVGhlIGFkZGl0aW9ucyBzaG93IHRoYXQgbW9zdCBkZXBhcnR1cmVzIGFuZCBhcnJpdmFscyBhcmUgbm90IGRlbGF5ZWQsCmFuZCB0aGF0IGZvciB0aGUgZmxpZ2h0cyBkZXBhcnRpbmcgY2xvc2UgdG8gb24gdGltZSB0aGVyZSBpcyB2ZXJ5CmxpdHRsZSByZWxhdGlvbnNoaXAgYmV0d2VlbiB0aGUgYXJyaXZhbCBhbmQgZGVwYXJ0dXJlIHRpbWVzOyB0aGV5IHNlZW0KdG8gYmUgbmVhcmx5IGluZGVwZW5kZW50LgoKQm90aCB0aGUgbWFyZ2luYWwgZGVuc2l0eSBlc3RpbWF0ZSBmb3IgdGhlIGRlcGFydHVyZSBkZWxheXMgYW5kIHRoZQpqb2ludCBkZW5zaXR5IGVzdGltYXRlcyBzdWdnZXN0IHNvbWUgc2xpZ2h0bHkgdW51c3VhbCBiZWhhdmlvciBhdCB0aGUKemVybyBwb2ludC4KCgojIyAzLiBXaW5kIFNwZWVkLCBUaW1lIG9mIERheSwgYW5kIERlcGFydHVyZSBEZWxheXMKCkpvaW4gdGhlIGB3ZWF0aGVyYCBkYXRhIHRvIHRoZSBgZmxpZ2h0c2AgZGF0YSB1c2luZyBgb3JpZ2luYCBhbmQKYHRpbWVfaG91cmAgYXMgdGhlIGtleS4gQnJpbmcgaW4gb25seSB0aGUgdmFyaWFibGVzIHdlIG5lZWQ6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtc2hvdyJ9CmZsIDwtIGxlZnRfam9pbihmbGlnaHRzLCBzZWxlY3Qod2VhdGhlciwgb3JpZ2luLCB0aW1lX2hvdXIsIHdpbmRfc3BlZWQpLAogICAgICAgICAgICAgICAgYygib3JpZ2luIiwgInRpbWVfaG91ciIpKQpgYGAKCkNoZWNrIHRoYXQgdGhpcyBrZXkgaXMgYSBnb29kIHByaW1hcnkga2V5IGZvciB0aGUgd2VhdGhlciB0YWJsZToKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1zaG93In0KbnJvdyhmaWx0ZXIoY291bnQod2VhdGhlciwgb3JpZ2luLCB0aW1lX2hvdXIpLCBuID4gMSkpCighIGFueU5BKHdlYXRoZXIkb3JpZ2luKSkgJiAoISBhbnlOQSh3ZWF0aGVyJHRpbWVfaG91cikpCmBgYAoKSW5jbHVkZSBvbmx5IHN1bW1lciBtb250aHMsIGFuZCBkcm9wIHJvd3Mgd2l0aCBtaXNzaW5nIHZhbHVlcyBvciB3aGVyZQp0aGUgd2luZCBzcGVlZCBpcyBhYm92ZSAzMCBtcGg6CgpgYGB7ciwgY2xhc3Muc291cmNlID0gImZvbGQtc2hvdyJ9CmxpYnJhcnkodGlkeXIpCmZscyA8LSBmaWx0ZXIoZmwsIG1vbnRoICVpbiUgNjo4KSB8PgogICAgZHJvcF9uYSgpIHw+CiAgICBmaWx0ZXIod2luZF9zcGVlZCA8PSAzMCkKYGBgCgpBIHBsb3Qgb2YgdGhlIHByb3BvcnRpb24gb2YgZGVwYXJ0dXJlcyB0aGF0IGFyZSBkZWxheWVkIGF0IGVhY2ggd2luZApzcGVlZDoKCmBgYHtyfQpncm91cF9ieShmbHMsIHdpbmRfc3BlZWQpIHw+CiAgICBzdW1tYXJpemUocF9kZWxheSA9IG1lYW4oZGVwX2RlbGF5ID4gMCksIG4gPSBuKCkpIHw+CiAgICB1bmdyb3VwKCkgfD4KICAgIGdncGxvdChhZXMod2luZF9zcGVlZCwgcF9kZWxheSkpICsKICAgIGdlb21fcG9pbnQoKSArCiAgICBnZW9tX3Ntb290aChhZXMod2VpZ2h0ID0gbikpCmBgYAoKVGhlcmUgYXBwZWFycyB0byBiZSBhbiBpbmNyZWFzZSBpbiB0aGUgcHJvcG9ydGlvbiBvZiBkZWxheWVkCmRlcGFydHVyZXMgYXNzb2NpYXRlZCB3aXRoIGFuIGluY3JlYXNlIGluIHdpbmQgc3BlZWQuCgpIb3dldmVyLCBhIGNvcGxvdCBvZiB0aGUgcHJvcG9ydGlvbiBvZiBkZWxheWVkIGRlcGFydHVyZXMgYWdhaW5zdApkZXBhcnR1cmUgaG91ciBjb25kaXRpb25lZCBvbiB3aW5kIHNwZWVkIHNob3dzIHRoYXQgdGhlcmUgaXMgYWxzbyBhCnBvc2l0aXZlIGFzc29jaWF0aW9uIHdpdGggdGhlIGRlcGFydHVyZSBob3VyLCBhbmQgdGhhdCBhc3NvY2lhdGlvbgpkb2VzIG5vdCB2YXJ5IG11Y2ggd2l0aCB3aW5kIHNwZWVkOgoKYGBge3J9Cmdyb3VwX2J5KGZscywgd2luZF9zcGVlZCwgaG91cikgfD4KICAgIHN1bW1hcml6ZShwX2RlbGF5ID0gbWVhbihkZXBfZGVsYXkgPiAwKSwgbiA9IG4oKSkgfD4KICAgIHVuZ3JvdXAoKSB8PgogICAgZ2dwbG90KGFlcyhob3VyLCBwX2RlbGF5KSkgKwogICAgZ2VvbV9wb2ludCgpICsKICAgIGdlb21fc21vb3RoKGFlcyh3ZWlnaHQgPSBuKSkgKwogICAgZmFjZXRfd3JhcCh+IGN1dF9udW1iZXIod2luZF9zcGVlZCwgNikpCmBgYAoKQSByZWFzb24gbWF5IGJlIHRoYXQgd2luZCBzcGVlZCBpbmNyZWFzZXMgdGhyb3VnaG91dCB0aGUgZGF5IHVudGlsCmFyb3VuZCA1IFBNICgxNzowMCBob3Vycyk6CgpgYGB7cn0KZ2dwbG90KGZscywgYWVzKGhvdXIsIHdpbmRfc3BlZWQpKSArIGdlb21fc21vb3RoKCkKYGBgCgpUaGUgY29wbG90IHNob3dzIHRoYXQgdGhlIHByb3BvcnRpb24gb2YgZGVsYXllZCBkZXBhcnR1cmVzCmluY3JlYXNlcyByb3VnaGx5IGxpbmVhcmx5IHVudGlsIGFyb3VuZCA1IFBNIGZvciBhbGwgd2luZCBzcGVlZApyYW5nZXMuIEEgbGluZWFyIHJlZ3Jlc3Npb24gb2YgdGhlIHByb3BvcnRpb24gb2YgZGVsYXllZCBkZXBhcnR1cmVzCmFnYWluc3QgYGhvdXJgIGFuZCBgd2luZF9zcGVlZGAgZm9yIGRlcGFydHVyZXMgcHJpb3IgdG8gNSBQTSBzaG93cyBhCnZlcnkgc21hbGwgY29lZmZpY2llbnQgZm9yIHdpbmQgc3BlZWQgb25jZSB0aW1lIG9mIGRheSBpcyBhY2NvdW50ZWQKZm9yOgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLXNob3cifQpmbHNfcHJvcCA8LSBncm91cF9ieShmbHMsIHdpbmRfc3BlZWQsIGhvdXIpIHw+CiAgICBzdW1tYXJpemUocF9kZWxheSA9IG1lYW4oZGVwX2RlbGF5ID4gMCksIG4gPSBuKCkpIHw+CiAgICB1bmdyb3VwKCkgfD4KICAgIGZpbHRlcihob3VyIDw9IDE3KQpsbShwX2RlbGF5IH4gaG91ciArIHdpbmRfc3BlZWQsIHdlaWdodHMgPSBuLCBkYXRhID0gZmxzX3Byb3ApCmBgYAo=










