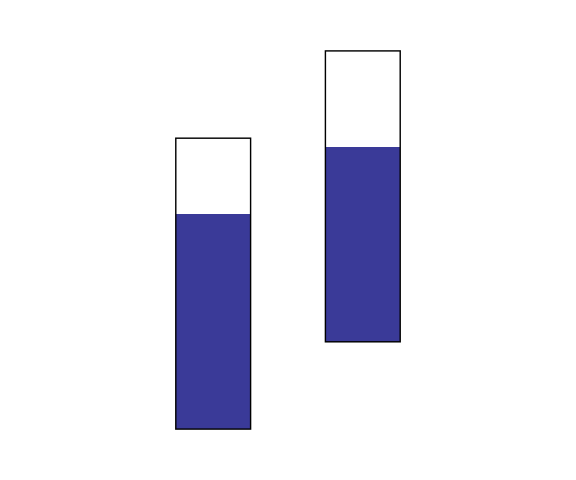Some River Flow Data
river <- scan("https://www.stat.uiowa.edu/~luke/data/river.dat")
plot(river)
A Simple Model of Visual Perception
The eyes acquire an image, which is processed through three stages of memory:
Iconic Memory
The first processing stage of an image happens in iconic memory.
Images remain in iconic memory for less than a second.
Processing in iconic memory is massively parallel and automatic.
This is called preattentive processing .
Preattentive processing is a fast recognition process.
Working Memory
Meaningful visual chunks are moved from iconic memory to short term memory.
These chunks are used by conscious, or attentive, processing.
Attentive processing often involves conscious comparisons or search.
Short term memory is limited:
Chunks can be of varying size; a coherent pattern can form a single chunk even if it is quite large.
If more chunks are needed or chunks are needed longer they need to be reacquired or retrieved from long term memory.
Long Term Memory
Long term visual memory is built up over a lifetime, though infrequently used visual chunks may become lost.
Chunks processed repeatedly in working memory may be transferred to long term memory.
Common patterns and contextual information can be retrieved from long term memory for attentive processing in working memory.
Visual Design Implications
Try to make as much use of preattentive features as possible.
Recognize when preattentive features might mislead.
For features that require attentive processing keep in mind that working memory is limited.
Some Examples of Challenges
Context Matters
Which of the inner circles is larger, or are they the same size?
Which of the lines is longer, or are they the same length?
The sine Illusion: which of the bars are longer, or are they the same length?
x <- seq(0, 5 * pi, length.out = 100)
w <- 0.5
plot(x, sin(x), ylim = c(-1, 1 + w), type = "n")
segments(x0 = x, y0 = sin(x), y1 = sin(x) + w, lwd = 3)
Which of the squares A and B is darker, or are they the same shade?
Some Optical Illusions
R implementations of some optical illusions by Kohske Takahashi:
Are these lines parallel?
Again, are these lines parallel?
Scintillating grid illusion : Black dots at the intersections appear and disappear; are they real?
Hermann grid illusion : “Ghost-like” grey blobs at the intersections of white lines.
Grid illusion in a cartogram:
A case where there are more dots than we can see at once:
Red from black and white:
Some illusions in pictures:
A large collection of optical illusions is available at https://michaelbach.de/ot/index.html .
Motion
n <- 50
x <- 2 * (1 : n)
y <- rep(2, n)
lim <- c(min(x) + 0.1 * (max(x) - min(x)), max(x) - 0.1 * (max(x) - min(x)))
v <- TRUE
for (i in 1 : 2) {
plot(x + v, y, xlim = lim)
v <- ! v
Sys.sleep(0.1)
}
Images contain no information about the direction of the rotation.
Your mind picks a direction.
library(rgl)
d <- data.frame(x = rnorm(1000), y = rnorm(1000), z = rnorm(1000))
points3d(d)
par3d(FOV = 1) ## removes perspective distortion
if (interactive())
play3d(spin3d(axis = c(0, 0, 1), rpm = 30), duration = 20)
Interactive rotation can help.
Depth cueing and perspective can also help.
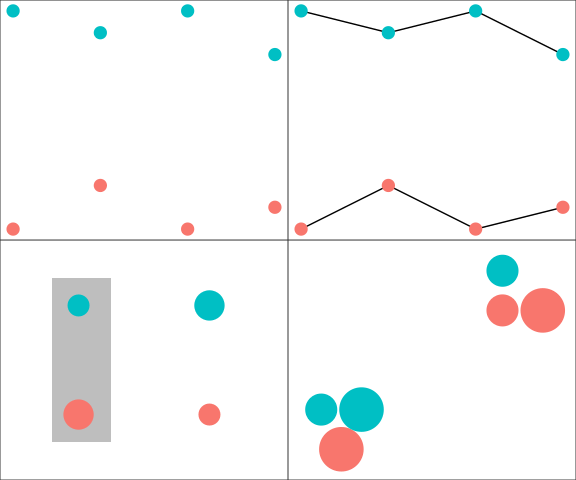
Popout and Distractors
Where is the red dot:
Shape only:
Shapes and colors:
Items, Attributes, Marks, and Channels
To evaluate or design a visualization it is useful to have some terms for the components.
Several schools have developed different but similar sets of terms.
Some References:
Bertin, J. (1967), The Semiology of Graphics .
Cleveland, W. S. (1988), The Elements of Graphing Data .
Cleveland, W. S. (1993), Visualizing Data .
Few, S. (2012), Show Me the Numbers: Designing Tables and Graphs to Enlighten , 2nd ed.
Munzner, T. (2014), Visualization Analysis and Design
Ware, C. (2012), Information Visualization: Perception for Design , 3rd ed.
Wilkinson, L. (2005), The Grammar of Graphics , 2nd ed.
Munzner uses the terminology of items , attributes , links , marks , and channels :
Items are the basic units on which data is collected: the entities represented by the rows in a tidy data frame.
Attributes are the numerical or categorical features of the data items we want to represent; the variables in a tidy data frame.
Links are relations among items: e.g. months within a year, or countries within a continent.
Marks are the geometric entities used to represent items: points, lines, areas. These correspond to the simple geom objects in ggplot.
Visual channels are features of marks that can be used to reflect values of attributes.
Channels correspond approximately to aesthetics in ggplot but are more focused on the visual aspect:
An x aesthetic that is transformed to polar coordinates is a different channel than an x aesthetic representing a position on a standard linear scale.
Channels are used to encode attributes (aesthetic mappings ).
A single attribute can be encoded in several channels.
Some channels are well suited to encode quantitative or ordered values; they are quantitatively perceived .
Others are only suited for nominal values.
A useful classification, adapted from Few(2012):
Form
Length
Yes
Width
Yes, but limited
Orientation
No
Size
Yes, but limited
Shape
No
Color
Hue
No
Intensity
Yes, but limited
Position
2D position
Yes
Munzner uses the terms magnitude channels and identity channels .
Ideally,
A useful principle: The most important attributes should be mapped to the most effective channels.
Channel Effectiveness
Some questions about channels:
What kind and how much information can a channel encode?
Are some channels better than others?
Can channels be used independently, or do they interfere?
Some criteria for evaluating channels:
Accuracy: How well can a viewer decode the information in the channel?
Discriminability: How easily can differences between attribute levels be perceived?
Separability: Can channels be used independently or is there interference?
Popout: can a channel provide popout where a difference is perceived preattentively?
Grouping: can a channel show perceptual grouping of items?
Channel Accuracy
Stevens (1957) argues that accuracy of magnitude channels can be described by a power law:
\[ \text{perceived sensation} = (\text{physical intensity})^\gamma \]
Experiments by Stevens suggest these values for some visual channels:
Others have raised concerns about the validity of these findings.
Another approach has used controlled experiments to assess accuracy of various channels used in visualizations:
William S. Cleveland and Robert McGill (1984), “Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods,” Journal of the American Statistical Association 79, 531–554.
William S. Cleveland and Robert McGill (1987), “Graphical Perception: The Visual Decoding of Quantitative Information on Graphical Displays of Data” Journal of the Royal Statistical Society. Series A , 192-229.
Jeffrey Heer and Michael Bostock (2010) “Crowdsourcing Graphical Perception: Using Mechanical Turk to Assess Visualization Design,” Proceedings of the SIGCHI , 203-212.
Munzner’s ordering by accuracy:
perceptual ladder .
Line width is another channel; not sure there is agreement on its accuracy, but it is not high.
Discriminability
Many channels, in particular identity channels, can only support a limited number of discriminable levels.
Line width is one of the most limited with perhaps 3 levels.
Using more than 5 or 6 color hues is not recommended.
Similarly, using more than 5 or 6 symbol shapes can create difficulties.
If the number of levels that can be represented by a channel is smaller than the number of attribute levels then some form of meaningful aggregation is needed.
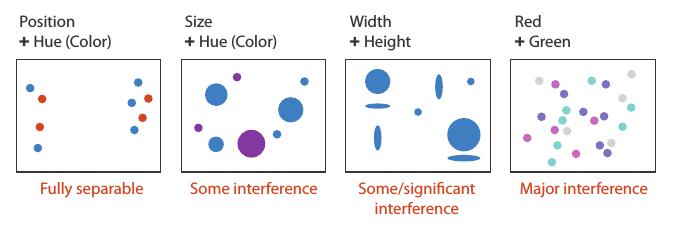
Separability
Some encodings can be used independently of each other; others interfere with each other to some degree.
Vertical an horizontal position can be used independently.
Color (hue) and position can be used independently
Size and hue interfere somewhat; hue is harder to perceive on smaller objects.
Width and height do not function well independently; the result is perceived primarily as shape.
Encoding two different values in the red and green channels as a hue does not work at all.
Popout
Many channels support visual popout : having one item or a few items immediately stand out from the others.
Annotation can also be used to create popout.
Grouping
Perceptual grouping can be achieved in several ways:
Experimental Evidence
Cleveland-McGill
The 1984 paper is available from JSTOR .
The paper formulates a theory for ranking Elementary Perceptual Tasks ; these correspond to channel mappings.
Some orderings were addressed by informal experiments (obvious to the authors at least).
Others were assessed by formal experiments with about 50 subjects.
Experiments focused on accuracy of decoding, though this is not viewed as the primary purpose of a graph:
One must be careful not to fall into a conceptual trap of adopting accuracy as a criterion. … The power of a graph is its ability to enable one to take in the quantitative information, organize it, and see patterns and structure not readily revealed by other means of studying the data.
Their premise:
A graphical form that involves elementary perceptual tasks that lead to more accurate judgments than another graphical form (with the same quantitative information) will result in better organization and increase the chances of a correct perception of patterns and behavior."
The tasks: For each setting
Results:
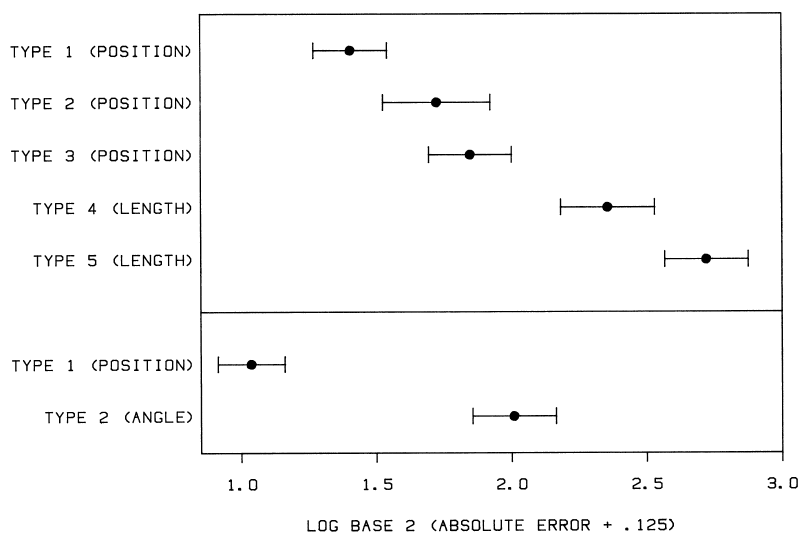
Percent large errors:
Absolute error:
Heer and Bostock
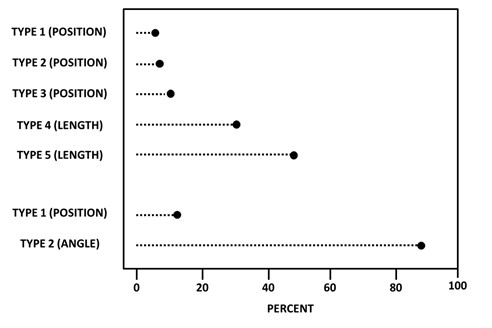
Heer and Bostock (2010) set out to replicate the Cleveland McGill experiment using crowd sourcing via Amazon Mechanical Turk
They used the five position stimuli from Cleveland and McGill and some new ones:
50 subjects were recruited for each task.
Results were consistent with Cleveland-McGill results:
Use of Mechanical Turk was deemed a success.
Pie Chart Experiments
Pie charts are popular but somewhat controversial.
Pie charts are inferior for comparisons to bar charts.
Pie charts are quite good at representing part-whole relationships.
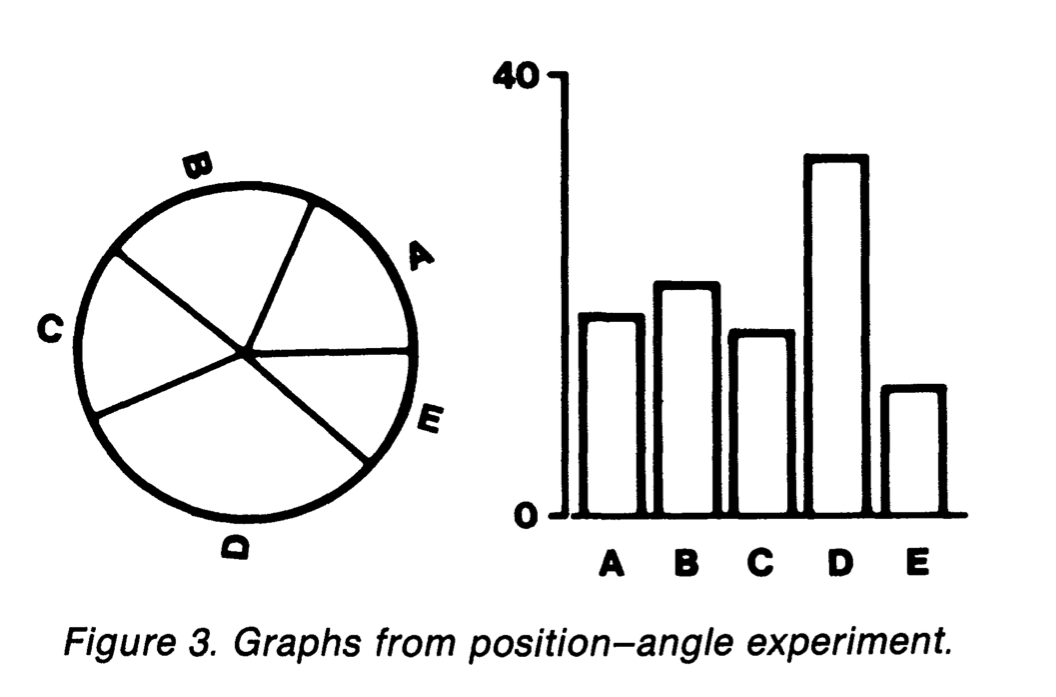
Cleveland and McGill suggested pie charts are read by angle.
Kosara and Skau report experiments that suggest this is not the case.
If it were, donut charts
Kosara’s blog provides a review of other pie chart studies.
Improving Some Common Charts
Cleveland and McGill set out to suggest improvements to some common charts. This is a selection of their examples.
Dot Charts
Cleveland and McGill use their perceptual ladder to argue strongly for using dot charts in place of bar charts and pie charts.
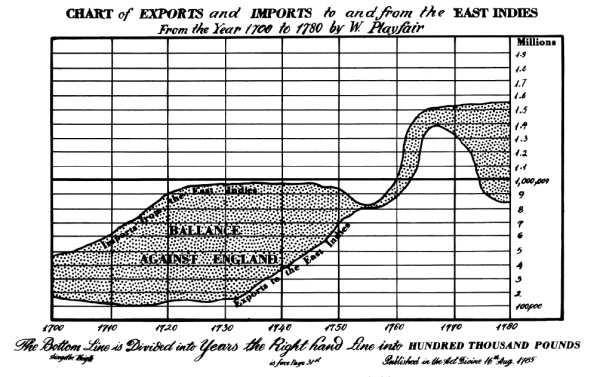
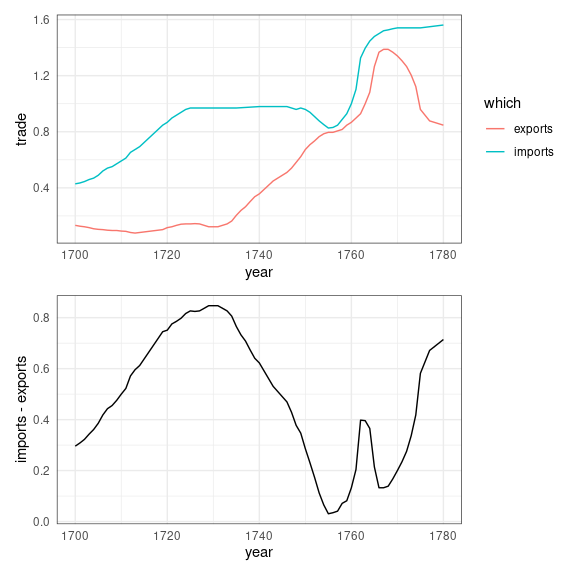
Playfair’s Balance of Trade plots
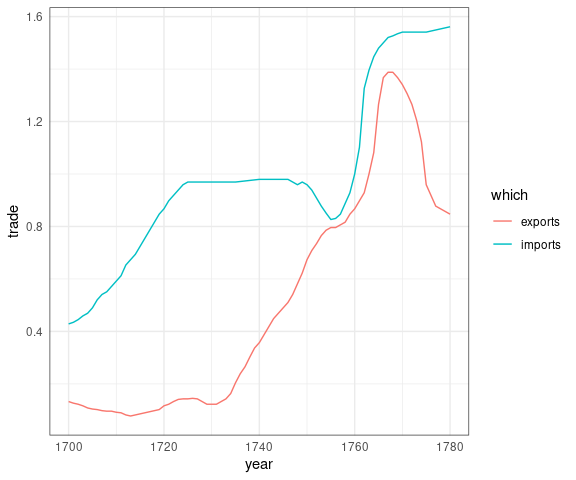
Playfair presented a number of plots showing imports and exports between England and other nations.
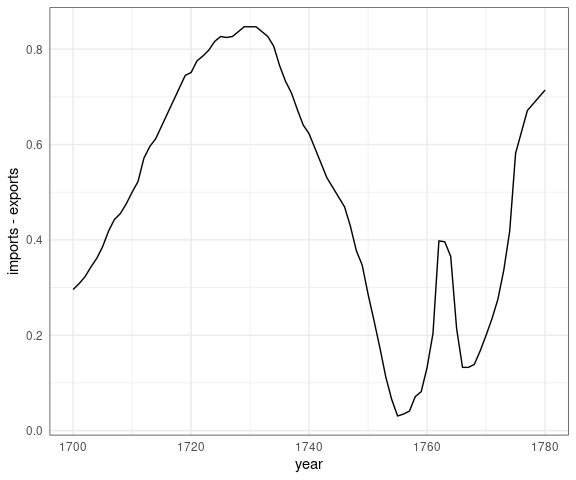
A primary goal was to show the balance of trade, the difference between exports and imports:
Assessing the differences from a plot showing exports and imports as separate curves requires length judgments, which are less accurate than comparisons to a common stale.
Plotting the difference makes the balance of trade much easier to assess:
An ensemble plot showing both views may also help.
Framed Unaligned Bars
It is difficult to compare lengths of unaligned rectangles when the lengths are close.
Adding a frame moves the task up the perceptual ladder to an unaligned comparison against a common scale.
Comparing to a common scale is still the most effective approach:
But this does suggest that using unaligned framed rectangles to encode a third variable, with position encoding the two primary variables may be effective.
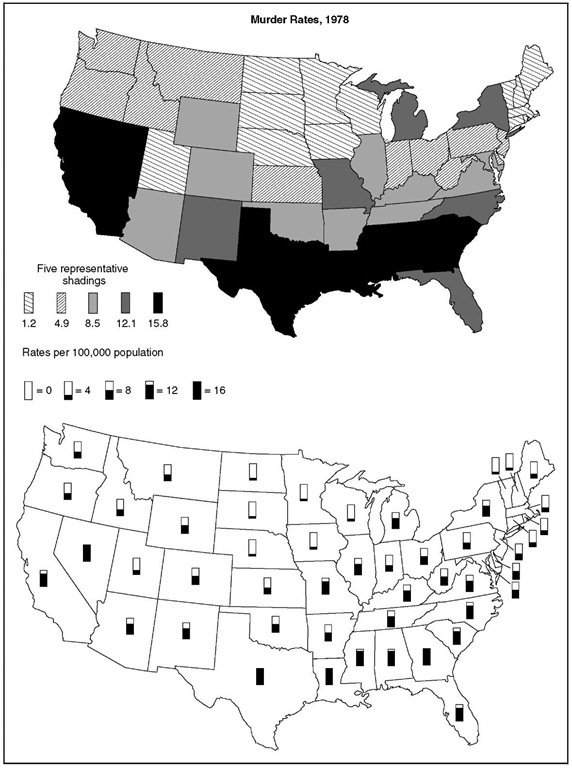
Framed Rectangle Maps
A choropleth map is a common way to depict a quantitative variable in a geographic context.
Shading is quite low on the perceptual ladder.
Cleveland and McGill suggest the use of framed rectangles positioned on the map as an alternative.
This does not seem to have caught on so far, though you do sometimes see the use of other glyphs, such as pie charts.
Analyzing a Design
Graph layout involves several levels:
A useful structure for describing the primary features:
What are the data items?
What are the attributes?
What marks are used?
What channels are used?
Which attribute is matched to channel 1
Which attribute is matched to channel 2
…
Useful questions:
Are the most important attributes mapped to the strongest channels?
Do the mappings do a good job of conveying the primary message?
If not, can the graph be improved by adjusting the mappings?
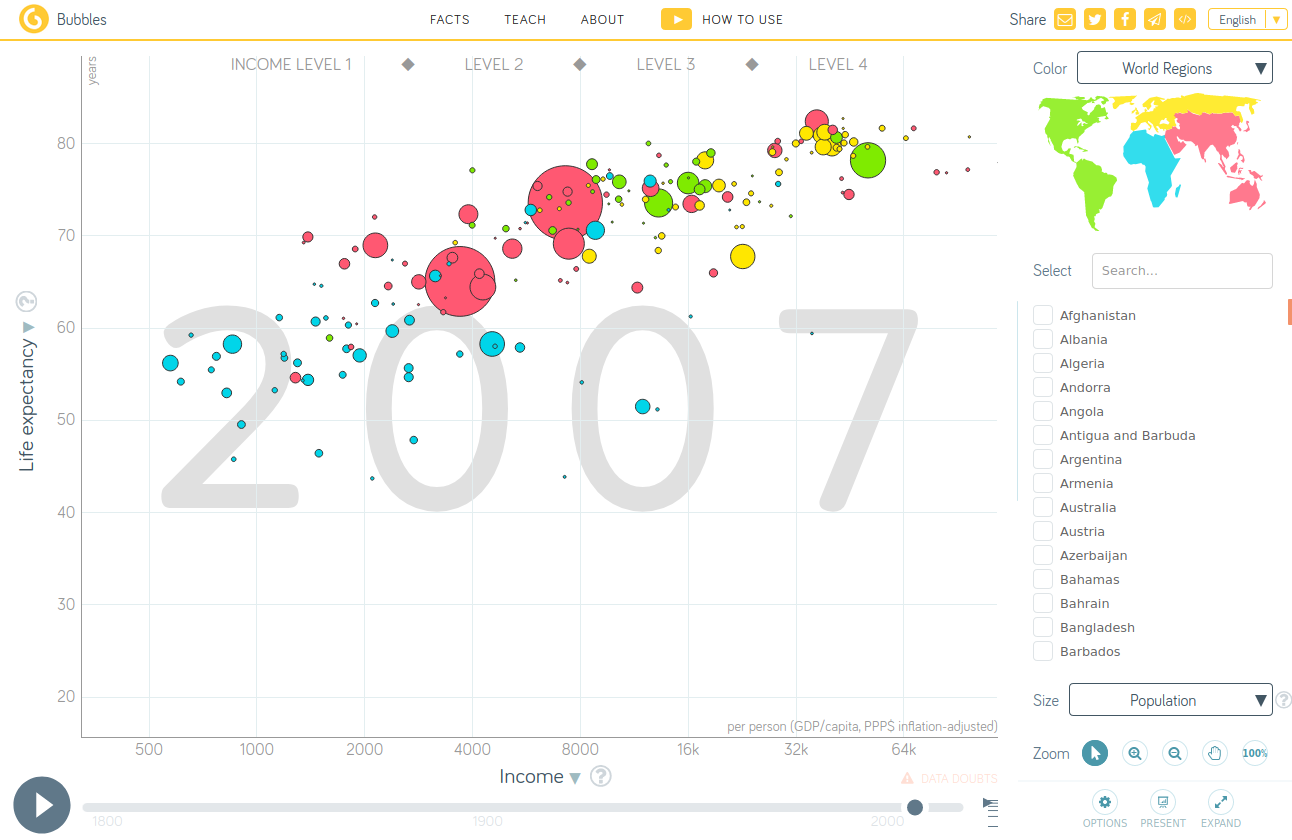
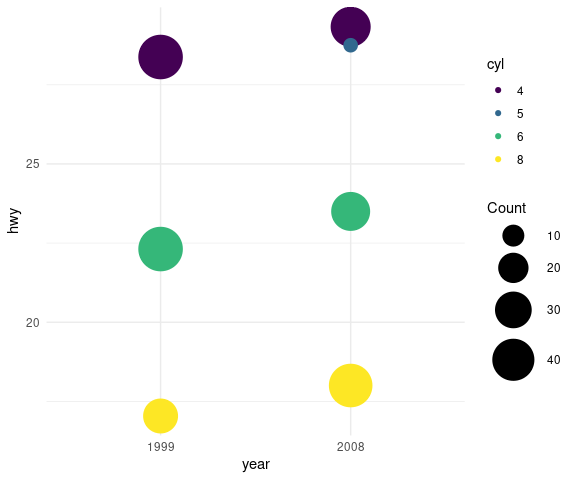
A Gapminder Plot
One of the frames of a plot from the GapMinder site :
The basic plot can be created with ggplot and aesthetic mappings:
library(gapminder)
gm2007 <- filter(gapminder, year == 2007)
ggplot(gm2007) +
geom_point(aes(x = gdpPercap,
y = lifeExp,
size = pop,
color = continent)) +
scale_x_log10() +
ylim(c(20, 85))
The data in the gapminder package differ somewhat from the data used by the Gapminder site, but overall the plot designs are very close.
With some adjustments the basic plot can be brought close to the Gapminder version in appearance:
gm2007 <- filter(gapminder, year == 2007) |>
arrange(desc(pop)) ## sort to avoid over-plotting
ggplot(gm2007) +
geom_point(aes(x = gdpPercap,
y = lifeExp,
size = pop,
fill = continent),
shape = 21) + ## to allow the using `fill` aesthetic
scale_x_log10(labels = comma) +
ylim(c(20, 85)) +
scale_size_area(max_size = 20,
labels = comma,
breaks = c(0.25 * 10 ^ 9, 0.5 * 10 ^ 9, 10 ^ 9)) +
scale_fill_manual(values = c(Africa = "deepskyblue",
Asia = "red",
Americas = "green",
Europe = "gold",
Oceania = "brown")) +
labs(x = "Income", y = "Life expectancy") +
theme(text = element_text(size = 16)) +
guides(fill = guide_legend(title = "Continent",
override.aes = list(size = 5),
order = 1),
size = guide_legend(title = "Population",
label.hjust = 1,
order = 2)) +
theme_minimal() +
theme(panel.border = element_rect(fill = NA, color = "grey20"))
Some notes:
Using larger bubbles makes the plot more engaging.
Using larger bubbles makes differences in population easier to assess, but makes the strength of the relationship between life expectancy and income harder to assess.
Using larger bubbles also increases the risk of over-plotting. Sorting the rows so larger bubble are drawn first helps reduce the risk somewhat.
These plots show a fairly strong marginal association between life expectancy and income.
There does not seem to be a strong association of population with the other two variables, but these plots are not ideal for that assessment.
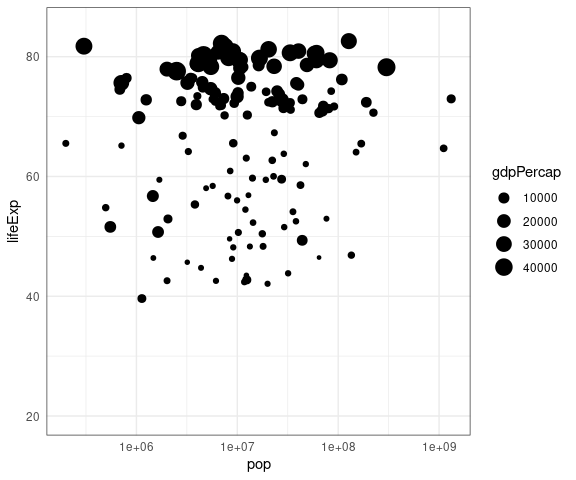
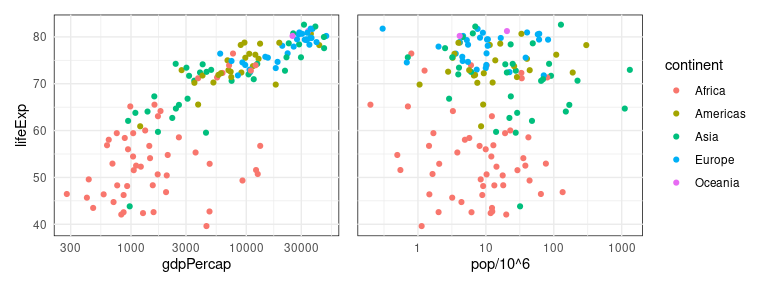
To judge the marginal association between life expectancy and population size we can change the channel mapping:
map the horizontal axis to population;
map area to income.
ggplot(filter(gapminder, year == 2007)) +
geom_point(aes(x = pop,
y = lifeExp,
size = gdpPercap)) +
scale_x_log10() +
ylim(c(20, 85)) +
theme_minimal() +
theme(panel.border =
element_rect(fill = NA,
color = "grey20"))
This confirms that there is very little association between life expectancy and population.
The association between life expectancy and income is still visible, but is easier to assess when these two variables are mapped to 2D position.
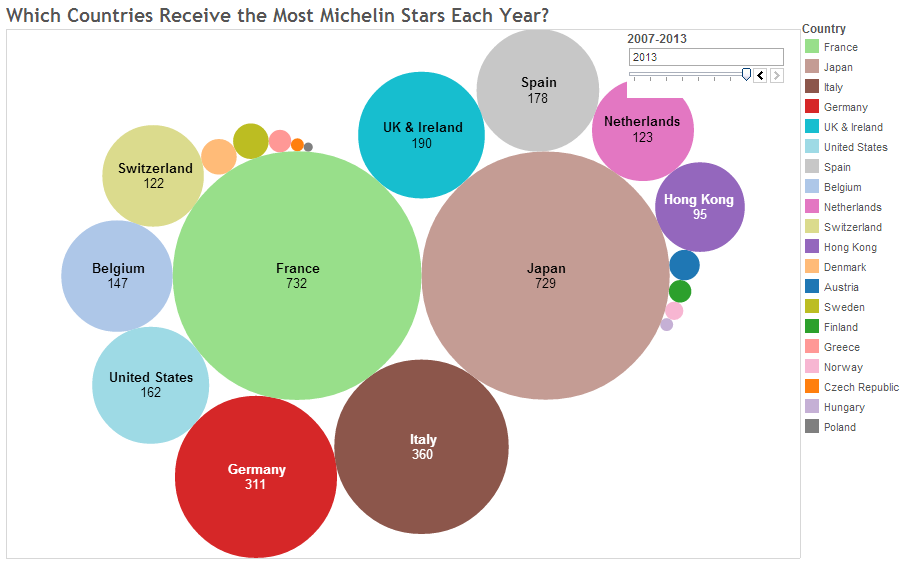
Michelin Stars
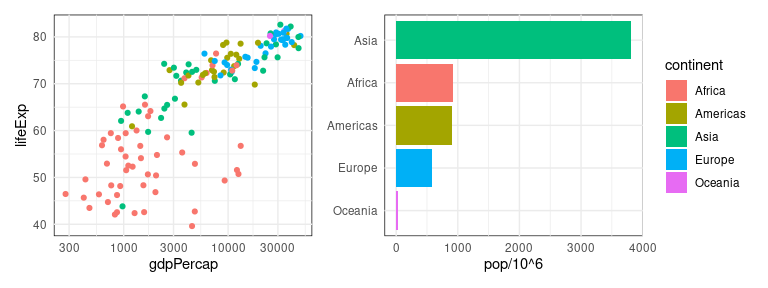
This image, from a blog post , shows the total number of stars for different countries:
Observations:
None of the channels are very strong.
The strongest channels, 2D position, are not used.
The number of colors used is too high.
A simple dot plot would convey the distribution better.
A dot plot using 2017 data from an article in The Telegraph:
michelin <- read.table(WLNK("michelin.dat"),
head = TRUE)
michelin <- mutate(michelin,
stars = one + 2 * two + 3 * three,
country = reorder(country, stars))
ggplot(michelin, aes(x = stars, y = country)) +
geom_point() +
labs(x = "Stars", y = NULL) +
theme_minimal() +
theme(text = element_text(size = 16)) +
theme(panel.border =
element_rect(fill = NA,
color = "grey20"))
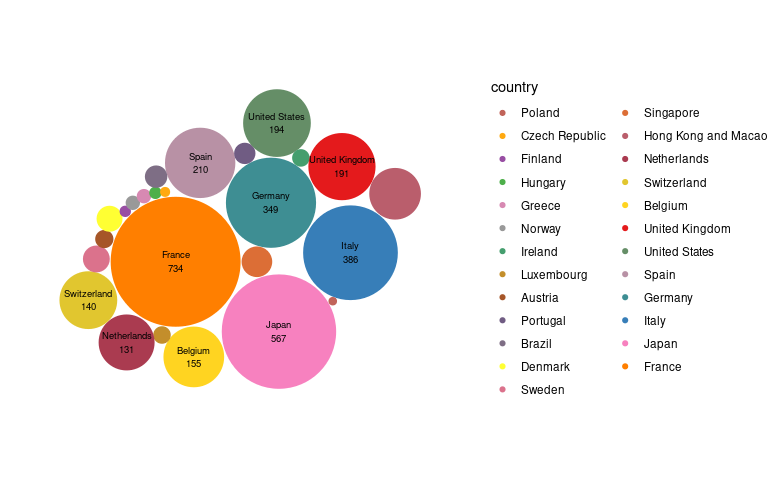
Even if a bubble plot is desired for aesthetic reasons, position could be used to
group countries by continent;
show countries on a map.
A plot like the original can be constructed by
computing locations for a set of packed spheres with specified radii;
using geom_point and geom_text.
## create randomly located packed spheres with specified areas
library(packcircles)
set.seed(54321)
packing <- circleProgressiveLayout(michelin$stars)
## merge circle locations with starts data
mcirc <- bind_cols(packing, michelin) |>
mutate(country = factor(country)) ## clean out stray attributes
## compute some colors to use
nr <- nrow(mcirc)
pal <- colorRampPalette(RColorBrewer::brewer.pal(9, "Set1"))
cols <- sample(pal(nr), nr)
## these need tuning for the screen or R markdown
csize <- 45
tsize <- 2.5
## the basic plot
## uses shape = 19 and `color` aesthetic
p <- ggplot(mcirc, aes(x = x, y = y)) +
geom_point(aes(size = radius ^ 2, color = country), shape = 19) +
scale_size_area(max_size = csize) +
geom_text(aes(label = paste(country, stars, sep = "\n")),
data = filter(mcirc, stars >= 120),
size = tsize) +
coord_fixed()
## adjustments
p + guides(size = "none") +
scale_color_manual(values = cols) +
xlim(with(mcirc, range(x) + c(-1, 1) * max(radius))) +
ylim(with(mcirc, range(y) + c(-1, 1) * max(radius))) +
theme_void()
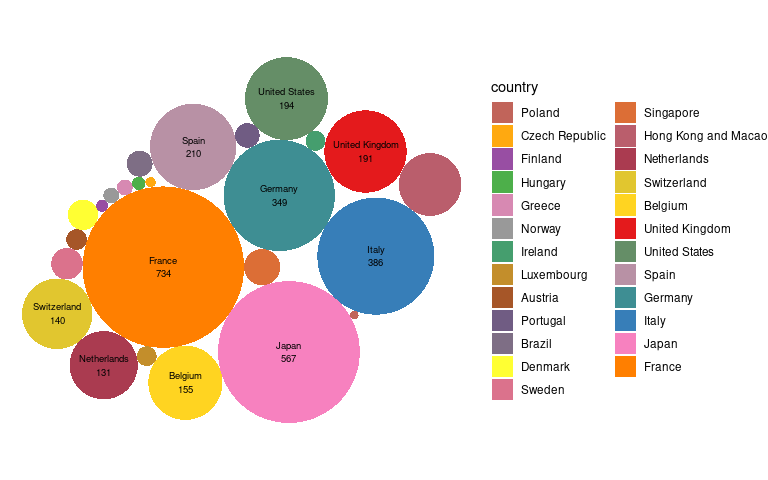
A somewhat more robust approach
creates vertex data for polygon approximations to the circles;
merges the stars data with the polygon data;
uses geom_polygon and geom_text.
This is very similar to the way simple choropleth maps are created.
## compute polygon approximations to spheres
mcircpoly <- circleLayoutVertices(mcirc, idcol = "country", npoints = 100) |>
rename(country = id)
## merge the stars data into the polygon data
sttab <- select(michelin, country, stars)
mcircpoly <- left_join(mcircpoly, sttab, "country")
## create the plot
ggplot(mcircpoly, aes(x = x, y = y)) +
geom_polygon(aes(fill = country)) +
geom_text(aes(label = paste(country, stars, sep = "\n")),
data = filter(mcirc, stars >= 120),
size = tsize) +
coord_fixed() +
scale_fill_manual(values = cols) +
theme_void()
Aspect Ratio and Perception
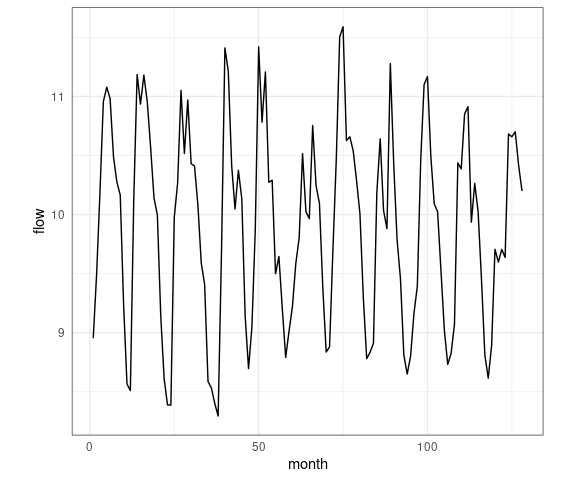
The river flow data shows how important aspect ratio can be to our ability to detect patterns:
Using a line plot the basic periodicity becomes apparent even in the first aspect ratio.
p2 <- p0 + geom_line()
p2 + coord_fixed(ratio = 35)
But the steeper increase/shallower decrease of most periods is easier to see in the second aspect ratio:
p2 + coord_fixed(ratio = 4)
The aspect ratio also influences interpretation of results.
Some alternative views of (suspect) data on the number of people on government assistance over a time period:
library(readr)
w <- read_csv(WLNK("hw2-welfare.csv"))
w <- mutate(w, onAssistance = onAssistance / 10 ^ 6)
w <- mutate(w,
date = seq(as.Date("2009-01-01"), by = "quarter", length.out = 10))
p0 <- ggplot(w, aes(x = date, y = onAssistance)) +
theme_minimal() +
theme(panel.border = element_rect(fill = NA, color = "grey20"))
p1 <- p0 + geom_line(aes(group = 1))
grid.arrange(p1, p1 + coord_fixed(ratio = 8),
p1 + ylim(0, max(w$onAssistance)),
p0 + geom_col(width = 40), ncol = 2)
Some notes:
Automated choices of axis scaling can affect the aspect ratio of the content of a plot.
A zero base line supports ratio comparisons.
The preattentive response to bar charts is always to compare ratios, so using a zero base line is important.
Using a non-zero base line for line plots and scatter plots encourages interval, or difference, comparisons.
Research on the effect of aspact ratio on perception has focused on accuracy of slope comparisons.
The general message is that keeping away from slopes that are too steep or too shallow is best.
Banking to 45 degrees , or choosing an aspect ratio so the slope magnitudes are distributed around 45 degrees is often recommended.
This also tends to be a useful “neutral ground” when political implications are involved.
Some references:
A blog post by Robert Kosara.
William S. Cleveland, Marylyn E. McGill and Robert McGill (1988), “The Shape Parameter of a Two-Variable Graph”, Journal of the American Statistical Association (JSTOR )
Justin Talbot, John Gerth, Pat Hanrahan (2012), “An Empirical Model of Slope Ratio Comparisons”, IEEE Trans. Visualization & Comp. Graphics (Proc. InfoVis) (PDF )
Ensemble Plots and Faceting
Using multiple channels allows a single plot to show a lot of information.
But over-plotting and interference can become problems.
One alternative is to use several related views in a useful arrangement.
Such arrangements are sometimes called ensemble plots .
There are a number of variations; a few are introduced below.
Similar Plots with Different Variables and Shared Encodings
One way to show three continuous variables is with two plots that share an axis:
library(patchwork)
pe_thm <- theme_minimal() +
theme(panel.background = element_rect(color = "black",
linewidth = 0.5,
fill = NA))
p1 <- ggplot(gm2007, aes(x = gdpPercap, y = lifeExp, color = continent)) +
geom_point() +
scale_x_log10() +
guides(color = "none") +
pe_thm
p2 <- ggplot(gm2007, aes(x = pop / 10 ^ 6, y = lifeExp, color = continent)) +
geom_point() +
scale_x_log10() +
pe_thm +
theme(axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
p1 + p2
Life expectancy is mapped to the vertical position in both plots.
Continent is mapped to color in both plots.
Guides can be shared when encodings are shared.
Different Plots with Shared Encodings
Multiple views of the data are often helpful.
Sharing encodings makes the relations between views easier to perceive.
p3 <- ggplot(gm2007,
aes(x = pop / 10 ^ 6,
y = reorder(continent, pop, FUN = sum),
fill = continent)) +
geom_col() +
ylab(NULL) +
pe_thm
p1 + p3
Small Multiples
Small multiples refers to a collection of plots with identical structure showing different subsets of the data and organized in a useful way.
These plot collections are also called trellis plots , lattice plots , or faceted plots .
A plot of life expectancy against income per capita in 2007 faceted by continent:
gd <- filter(gapminder, year %in% c(1977, 1987, 1997, 2007))
gd2007 <- filter(gapminder, year == 2007)
fct_thm <- theme_minimal() +
theme(panel.background = element_rect(color = "black",
linewidth = 0.5,
fill = NA))
ggplot(gd2007, aes(x = gdpPercap, y = lifeExp, color = continent)) +
geom_point(size = 2.5) +
scale_x_log10() +
facet_wrap(~ continent) +
fct_thm
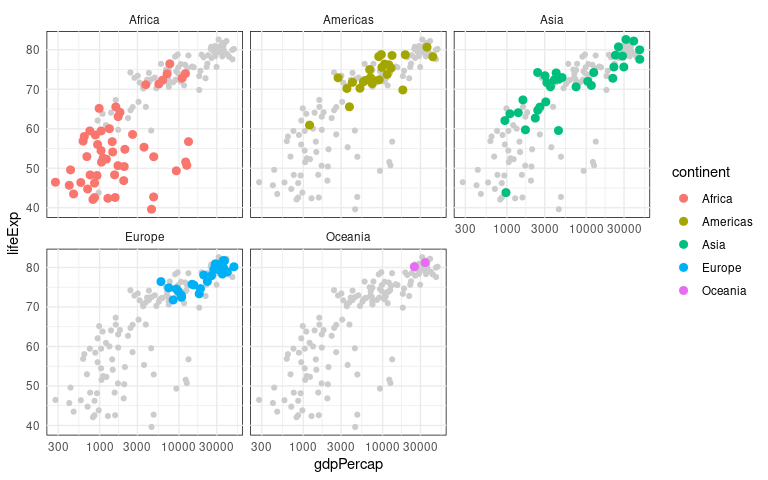
A useful variation is to show a muted view of the full data in the background:
ggplot(gd2007, aes(x = gdpPercap, y = lifeExp, color = continent)) +
geom_point(data = mutate(gd2007, continent = NULL), color = "grey80") +
geom_point(size = 2.5) +
scale_x_log10() +
facet_wrap(~ continent) +
fct_thm
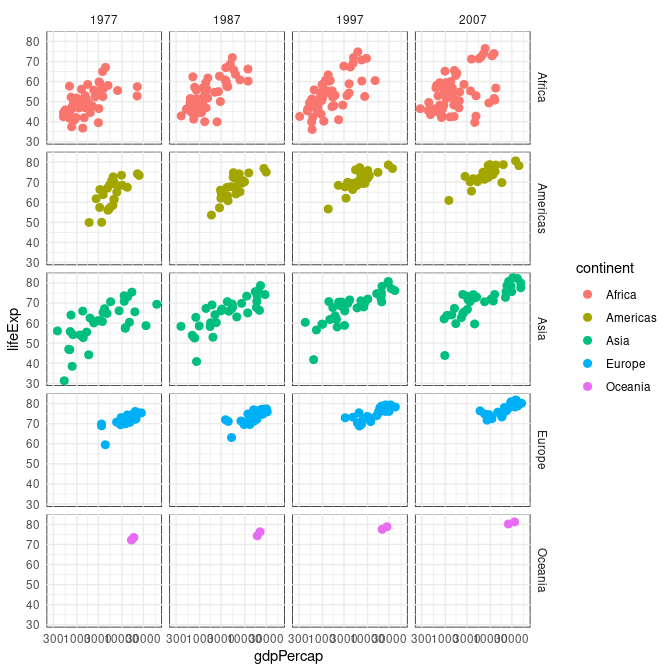
Data can be facetet on two variables.
This plot shows the full data faceted by both continent and a set of years:
ggplot(gd, aes(x = gdpPercap, y = lifeExp, color = continent)) +
geom_point(size = 2.5) +
scale_x_log10() +
facet_grid(continent ~ year) +
fct_thm
Adding muted data for each year helps regonizing where each continent group fits within a year
ggplot(gd, aes(x = gdpPercap, y = lifeExp, color = continent)) +
geom_point(data = mutate(gd, continent = NULL), color = "grey80") +
geom_point(size = 2.5) +
scale_x_log10() +
facet_grid(continent ~ year) +
fct_thm
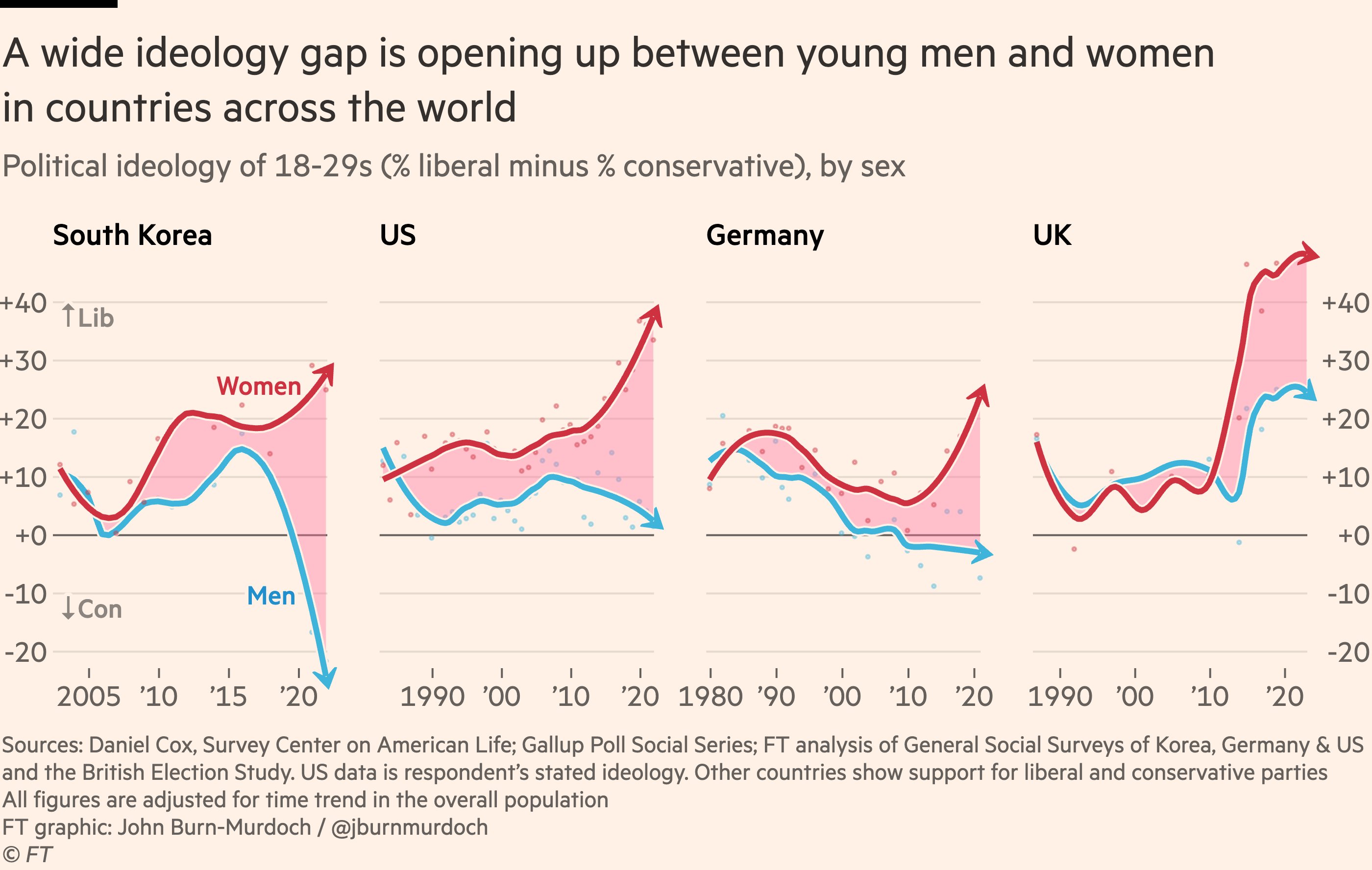
A recent example from the Financial Times:
Exercises
Which of the following channels are magnitude channels and which are identity channels?
Position on a common scale
Length
Color hue (red, green, etc.)
Symbol shape (dot, cross, etc.)
Consider the following visualizations of the 2017 Michelin star data:
Which plot makes it easier to compare the numbers of stars for different countries? Explain your conclusion by identifying the channels used and their relative strengths.
Identify the items, attributes, marks, channels, and mappings use in the following plot:
LS0tCnRpdGxlOiAiUGVyY2VwdGlvbiBhbmQgVmlzdWFsaXphdGlvbiIKb3V0cHV0OgogIGh0bWxfZG9jdW1lbnQ6CiAgICB0b2M6IHllcwogICAgY29kZV9mb2xkaW5nOiBzaG93CiAgICBjb2RlX2Rvd25sb2FkOiB0cnVlCi0tLQoKPGxpbmsgcmVsPSJzdHlsZXNoZWV0IiBocmVmPSJzdGF0NDU4MC5jc3MiIHR5cGU9InRleHQvY3NzIiAvPgoKYGBge3Igc2V0dXAsIGluY2x1ZGUgPSBGQUxTRX0Kc291cmNlKGhlcmU6OmhlcmUoInNldHVwLlIiKSkKa25pdHI6Om9wdHNfY2h1bmskc2V0KGNvbGxhcHNlID0gVFJVRSwgbWVzc2FnZSA9IEZBTFNFLAogICAgICAgICAgICAgICAgICAgICAgZmlnLmhlaWdodCA9IDUsIGZpZy53aWR0aCA9IDYsIGZpZy5hbGlnbiA9ICJjZW50ZXIiKQoKbGlicmFyeShsYXR0aWNlKQpsaWJyYXJ5KHRpZHl2ZXJzZSkKbGlicmFyeShncmlkRXh0cmEpCmxpYnJhcnkoc2NhbGVzKQpzZXQuc2VlZCgxMjM0NSkKYGBgCgoKIyMgU29tZSBSaXZlciBGbG93IERhdGEKCmBgYHtyLCBlY2hvID0gVFJVRX0Kcml2ZXIgPC0gc2NhbigiaHR0cHM6Ly93d3cuc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9yaXZlci5kYXQiKQpwbG90KHJpdmVyKQpgYGAKCgojIyBBIFNpbXBsZSBNb2RlbCBvZiBWaXN1YWwgUGVyY2VwdGlvbgoKVGhlIGV5ZXMgYWNxdWlyZSBhbiBpbWFnZSwgd2hpY2ggaXMgcHJvY2Vzc2VkIHRocm91Z2ggdGhyZWUgc3RhZ2VzIG9mCm1lbW9yeToKCiogSWNvbmljIG1lbW9yeTsKCiogV29ya2luZyBtZW1vcnksIG9yIHNob3J0LXRlcm0gbWVtb3J5OwoKKiBMb25nLXRlcm0gbWVtb3J5LgoKCiMjIyBJY29uaWMgTWVtb3J5CgpUaGUgZmlyc3QgcHJvY2Vzc2luZyBzdGFnZSBvZiBhbiBpbWFnZSBoYXBwZW5zIGluIGljb25pYyBtZW1vcnkuCgoqIEltYWdlcyByZW1haW4gaW4gaWNvbmljIG1lbW9yeSBmb3IgbGVzcyB0aGFuIGEgc2Vjb25kLgoKKiBQcm9jZXNzaW5nIGluIGljb25pYyBtZW1vcnkgaXMgbWFzc2l2ZWx5IHBhcmFsbGVsIGFuZCBhdXRvbWF0aWMuCgoqIFRoaXMgaXMgY2FsbGVkIF9wcmVhdHRlbnRpdmUgcHJvY2Vzc2luZ18uCgpQcmVhdHRlbnRpdmUgcHJvY2Vzc2luZyBpcyBhIGZhc3QgcmVjb2duaXRpb24gcHJvY2Vzcy4KCgojIyMgV29ya2luZyBNZW1vcnkKCk1lYW5pbmdmdWwgdmlzdWFsIGNodW5rcyBhcmUgbW92ZWQgZnJvbSBpY29uaWMgbWVtb3J5IHRvIHNob3J0IHRlcm0gbWVtb3J5LgoKVGhlc2UgY2h1bmtzIGFyZSB1c2VkIGJ5IGNvbnNjaW91cywgb3IgYXR0ZW50aXZlLCBwcm9jZXNzaW5nLgoKQXR0ZW50aXZlIHByb2Nlc3Npbmcgb2Z0ZW4gaW52b2x2ZXMgY29uc2Npb3VzIGNvbXBhcmlzb25zIG9yIHNlYXJjaC4KClNob3J0IHRlcm0gbWVtb3J5IGlzIGxpbWl0ZWQ6CgoqIGluZm9ybWF0aW9uIGlzIHJldGFpbmVkIGZvciBvbmx5IGEgZmV3IHNlY29uZHM7CgoqIG9ubHkgdGhyZWUgb3IgZm91cnMgY2h1bmtzIGNhbiBiZSBoZWxkIGF0IGEgdGltZS4KCkNodW5rcyBjYW4gYmUgb2YgdmFyeWluZyBzaXplOyBhIGNvaGVyZW50IHBhdHRlcm4gY2FuIGZvcm0gYSBzaW5nbGUKY2h1bmsgZXZlbiBpZiBpdCBpcyBxdWl0ZSBsYXJnZS4KCklmIG1vcmUgY2h1bmtzIGFyZSBuZWVkZWQgb3IgY2h1bmtzIGFyZSBuZWVkZWQgbG9uZ2VyIHRoZXkgbmVlZCB0bwpiZSByZWFjcXVpcmVkIG9yIHJldHJpZXZlZCBmcm9tIGxvbmcgdGVybSBtZW1vcnkuCgoKIyMjIExvbmcgVGVybSBNZW1vcnkKCkxvbmcgdGVybSB2aXN1YWwgbWVtb3J5IGlzIGJ1aWx0IHVwIG92ZXIgYSBsaWZldGltZSwgdGhvdWdoCmluZnJlcXVlbnRseSB1c2VkIHZpc3VhbCBjaHVua3MgbWF5IGJlY29tZSBsb3N0LgoKQ2h1bmtzIHByb2Nlc3NlZCByZXBlYXRlZGx5IGluIHdvcmtpbmcgbWVtb3J5IG1heSBiZSB0cmFuc2ZlcnJlZCB0bwpsb25nIHRlcm0gbWVtb3J5LgoKQ29tbW9uIHBhdHRlcm5zIGFuZCBjb250ZXh0dWFsIGluZm9ybWF0aW9uIGNhbiBiZSByZXRyaWV2ZWQgZnJvbQpsb25nIHRlcm0gbWVtb3J5IGZvciBhdHRlbnRpdmUgcHJvY2Vzc2luZyBpbiB3b3JraW5nIG1lbW9yeS4KCgojIyMgVmlzdWFsIERlc2lnbiBJbXBsaWNhdGlvbnMKClRyeSB0byBtYWtlIGFzIG11Y2ggdXNlIG9mIHByZWF0dGVudGl2ZSBmZWF0dXJlcyBhcyBwb3NzaWJsZS4KClJlY29nbml6ZSB3aGVuIHByZWF0dGVudGl2ZSBmZWF0dXJlcyBtaWdodCBtaXNsZWFkLgoKRm9yIGZlYXR1cmVzIHRoYXQgcmVxdWlyZSBhdHRlbnRpdmUgcHJvY2Vzc2luZyBrZWVwIGluIG1pbmQgdGhhdAp3b3JraW5nIG1lbW9yeSBpcyBsaW1pdGVkLgoKCiMjIFNvbWUgRXhhbXBsZXMgb2YgQ2hhbGxlbmdlcwoKCiMjIyBDb250ZXh0IE1hdHRlcnMKCldoaWNoIG9mIHRoZSBpbm5lciBjaXJjbGVzIGlzIGxhcmdlciwgb3IgYXJlIHRoZXkgdGhlIHNhbWUgc2l6ZT8KCjwhLS0KaHR0cDovL2p1bmtjaGFydHMudHlwZXBhZC5jb20vanVua19jaGFydHMvMjAxMi8wOS9pbnN1ZmZpY2llbmN5LWFuZC1pbGx1c2lvbnMuaHRtbAotLT4KCmBgYHtyLCBlY2hvID0gRkFMU0V9CmNpcmNsZSA8LSBsb2NhbCh7CiAgICBwaGkgPC0gc2VxKDAsIDIgKiBwaSwgbGVuZ3RoLm91dCA9IDEwMCkKICAgIHggPC0gY29zKHBoaSkKICAgIHkgPC0gc2luKHBoaSkKICAgIGZ1bmN0aW9uKGN4ID0gMCwgY3kgPSAwLCByID0gMSkgbGlzdCh4ID0gciAqIHggKyBjeCwgeSA9IHIgKiB5ICsgY3kpCn0pCnNldHVwIDwtIGZ1bmN0aW9uKHcgPSA1KQogICAgcGxvdCgwLCB0eXBlID0gIm4iLCBhc3AgPSAxLAogICAgICAgICB4bGltID0gYygtdywgdyksIHlsaW0gPSBjKC13LCB3KSwKICAgICAgICAgYXhlcyA9IEZBTFNFLCB4bGFiID0gIiIsIHlsYWIgPSAiIiwKICAgICAgICAgbWFyID0gYygwLCAwLCAwLCAwKSkKc2V0dXAoKQpwb2x5Z29uKGNpcmNsZSgtMiwgMCwgMykpCnBvbHlnb24oY2lyY2xlKC0yLCAwKSwgY29sID0gImJsYWNrIikKcG9seWdvbihjaXJjbGUoMywgMCwgMS4zKSkKcG9seWdvbihjaXJjbGUoMywgMCksIGNvbCA9ICJibGFjayIpCmBgYApgYGB7ciwgZWNobyA9IEZBTFNFfQpzZXR1cCgxMCkKeDEgPC0gLTQKeDIgPC0gNgpwb2x5Z29uKGNpcmNsZSh4MSwgMCkpCmZvciAoYSBpbiAoMiAqIHBpICogKDEgOiA2KSAvIDYpKQogICAgcG9seWdvbihjaXJjbGUoNCAqIGNvcyhhKSArIHgxLCA0ICogc2luKGEpLCAyKSkKcG9seWdvbihjaXJjbGUoeDIsIDApKQpmb3IgKGEgaW4gKDIgKiBwaSAqICgxIDogMTApIC8gMTApKQogICAgcG9seWdvbihjaXJjbGUoMS41ICogY29zKGEpICsgeDIsIDEuNSAqIHNpbihhKSwgMC41KSkKYGBgCgpXaGljaCBvZiB0aGUgbGluZXMgaXMgbG9uZ2VyLCBvciBhcmUgdGhleSB0aGUgc2FtZSBsZW5ndGg/CgpgYGB7ciwgZWNobyA9IEZBTFNFfQpzZXR1cCgpCnBvbHlnb24oY2lyY2xlKC00LCAtMikpCnBvbHlnb24oY2lyY2xlKDQsIC0yKSkKcG9seWdvbihjaXJjbGUoLTIsIDIpKQpwb2x5Z29uKGNpcmNsZSgyLCAyKSkKc2VnbWVudHMoLTMsIC0yLCAzLCAtMiwgbHdkID0gMykKc2VnbWVudHMoLTMsICsyLCAzLCArMiwgbHdkID0gMykKCndpZHRoIDwtIDMKYWggPC0gZnVuY3Rpb24oeCwgeSwgc2l6ZSA9IDEsIGRpciA9IDEpIHsKICAgIGF4IDwtIGMoLXNpemUgKiBkaXIsIDAsIC1zaXplICogZGlyKQogICAgYXkgPC0gYygtc2l6ZSwgMCwgc2l6ZSkKICAgIGxpbmVzKHggKyBheCwgeSArIGF5LCBsd2QgPSB3aWR0aCkKfQpgYGAKYGBge3IsIGVjaG8gPSBGQUxTRX0Kc2V0dXAoKQpzZWdtZW50cygtMywgLTIsIDMsIC0yLCBsd2QgPSB3aWR0aCkKYWgoMywgLTIpCmFoKC0zLCAtMiwgZGlyID0gLTEpCnNlZ21lbnRzKC0zLCArMiwgMywgKzIsIGx3ZCA9IHdpZHRoKQphaCgzLCAyLCBkaXIgPSAtMSkKYWgoLTMsIDIpCmBgYAoKVGhlIHNpbmUgSWxsdXNpb246IHdoaWNoIG9mIHRoZSBiYXJzIGFyZSBsb25nZXIsIG9yIGFyZSB0aGV5IHRoZSBzYW1lCmxlbmd0aD8KCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KeCA8LSBzZXEoMCwgNSAqIHBpLCBsZW5ndGgub3V0ID0gMTAwKQp3IDwtIDAuNQpwbG90KHgsIHNpbih4KSwgeWxpbSA9IGMoLTEsIDEgKyB3KSwgdHlwZSA9ICJuIikKc2VnbWVudHMoeDAgPSB4LCB5MCA9IHNpbih4KSwgeTEgPSBzaW4oeCkgKyB3LCBsd2QgPSAzKQpgYGAKCjwhLS0gaHR0cDovL3ZhbnNlb2Rlc2lnbi5jb20vd2ViLWRlc2lnbi9jb2xvci1sdW1pbmFuY2UvLS0+CgpXaGljaCBvZiB0aGUgc3F1YXJlcyBBIGFuZCBCIGlzIGRhcmtlciwgb3IgYXJlIHRoZXkgdGhlIHNhbWUgc2hhZGU/CgpgYGB7ciBlY2hvID0gRkFMU0V9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiY2hlc3MxLnBuZyIpKQpgYGAKYGBge3IgZWNobyA9IEZBTFNFfQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoImNoZXNzMi5wbmciKSkKYGBgCgoKIyMjIFNvbWUgT3B0aWNhbCBJbGx1c2lvbnMKCltSIGltcGxlbWVudGF0aW9uc10oaHR0cDovL3JwdWJzLmNvbS9rb2hza2UvUi1kZS1pbGx1c2lvbikgb2Ygc29tZQpvcHRpY2FsIGlsbHVzaW9ucyBieSBLb2hza2UgVGFrYWhhc2hpOgoKPCEtLQpTb21lIGFsc28gdXNlZCBpbgpodHRwczovL2NyYW4uci1wcm9qZWN0Lm9yZy93ZWIvcGFja2FnZXMva25pdHJCb290c3RyYXAvdmlnbmV0dGVzL2lsbHVzaW9ucy5odG1sCgpGaXJzdCBzYXcgdGhlc2UgaW4KaHR0cDovL2Jsb2cucmV2b2x1dGlvbmFuYWx5dGljcy5jb20vMjAxMi8xMi9jcmVhdGUtb3B0aWNhbC1pbGx1c2lvbnMtd2l0aC1yLmh0bWwKLS0+CgpBcmUgdGhlc2UgbGluZXMgcGFyYWxsZWw/CgpgYGB7ciwgZWNobyA9IEZBTFNFfQpsaWJyYXJ5KGdyaWQpCnJzIDwtIGV4cGFuZC5ncmlkKHggPSBzZXEoMCwgMSwgMSAvIDEwKSwgeSA9IHNlcSgwLCAxLCAxIC8gMTApKQpncmlkLnJlY3QocnMkeCwgcnMkeSwgMSAvIDEwIC8gMiwgMSAvIDEwIC8gMiwKICAgICAgICAgIGdwID0gZ3BhcihmaWxsID0gImJsYWNrIiwgY29sID0gTkEpKQpncmlkLnJlY3QocnMkeCArIDEgLyAxMCAvIDQsIHJzJHkgKyAxIC8gMTAgLyAyLCAxIC8gMTAgLyAyLCAxIC8gMTAgLyAyLAogICAgICAgICAgZ3AgPSBncGFyKGZpbGwgPSAiYmxhY2siLCBjb2wgPSBOQSkpCmxzIDwtIGV4cGFuZC5ncmlkKHggPSAwIDogMSwgeSA9IHNlcSgwLCAxLCAxIC8gMjApIC0gMSAvIDIwIC8gMikKZ3JpZC5wb2x5bGluZShscyR4LCBscyR5LCBpZCA9IGdsKG5yb3cobHMpIC8gMiwgMiksCiAgICAgICAgICAgICAgZ3AgPSBncGFyKGNvbCA9ICJncmV5NTAiLCBsd2QgPSAxKSkKYGBgCgpBZ2FpbiwgYXJlIHRoZXNlIGxpbmVzIHBhcmFsbGVsPwoKYGBge3IsIGVjaG8gPSBGQUxTRX0KZ3JpZC5uZXdwYWdlKCkKbiA8LSAxMDsgbnkgPC0gODsgTCA8LSAwLjAxCmMgPC0gc2VxKDAsIDEsIGxlbmd0aCA9IG4pOyBkIDwtIDEuMiAqIGRpZmYoYylbMV0gLyAyCmNvbCA8LSBjKCJibGFjayIsICJ3aGl0ZSIpCnggPC0gYyhjIC0gZCwgYywgYyArIGQsIGMpCnkgPC0gcmVwKGMoMCwgLWQsIDAsIGQpLCBlYWNoID0gbikKdyA8LSBjKGMgLSBkLCBjIC0gZCArIEwsIGMgKyBkLCBjICsgZCAtIEwpCnogPC0gYygwLCBMLCAwLCAtTCkKeXMgPC0gc2VxKDAsIDEsIGxlbmd0aCA9IG55KQpncmlkLnJlY3QoZ3AgPSBncGFyKGZpbGwgPSBncmF5KDAuNSksIGNvbCA9IE5BKSkKcGx5cjo6bF9wbHkoMSA6IG55LCBmdW5jdGlvbihpKSB7CiAgICBpZiAoaSAlJSAyID09IDApIHsKICAgICAgICBjbyA8LSByZXYoY29sKQogICAgICAgIHogPC0gLXoKICAgIH0gZWxzZQogICAgICAgIGNvIDwtIGNvbAogICAgZ3JpZC5wb2x5Z29uKHgsIHkgKyB5c1tpXSwgaWQgPSByZXAoMSA6IG4sIDQpLAogICAgICAgICAgICAgICAgIGdwID0gZ3BhcihmaWxsID0gY28sIGNvbCA9IE5BKSkKICAgIGdyaWQucG9seWdvbih3LCByZXAoeiwgZWFjaCA9IG4pICsgeXNbaV0sIGlkID0gcmVwKDEgOiBuLCA0KSwKICAgICAgICAgICAgICAgICBncCA9IGdwYXIoZmlsbCA9IHJldihjbyksIGNvbCA9IE5BKSkKfSkKYGBgCgpbU2NpbnRpbGxhdGluZyBncmlkCmlsbHVzaW9uXShodHRwczovL3BzeWNob2xvZ3kuZmFuZG9tLmNvbS93aWtpL0dyaWRfaWxsdXNpb24jU2NpbnRpbGxhdGluZ19ncmlkX2lsbHVzaW9uKToKQmxhY2sgZG90cyBhdCB0aGUgaW50ZXJzZWN0aW9ucyBhcHBlYXIgYW5kIGRpc2FwcGVhcjsgYXJlIHRoZXkgcmVhbD8KCjwhLS0gdGhlIGNpcmNsZXMgbmVlZCB0byBiZSBhIGxpdHRsZSBiaWdnZXIgdGhhbiB0aGUgbGluZXMgLS0+CgpgYGB7ciwgZWNobyA9IEZBTFNFfQpueCA8LSA2OyBueSA8LSA2OyBsd2QgPC0gMTA7IGNyIDwtIDEuMiAvIDEwMApncmlkLm5ld3BhZ2UoKQojIyBub2xpbnQgc3RhcnQKIyMgeGxpbSA8LSB5bGltIDwtIGMoMC4wNSwgMC45NSkKIyMgcHVzaFZpZXdwb3J0KHZpZXdwb3J0KCAjIGxpa2UgcGxvdC53aW5kb3coKQojIyAgICAgICAgIHg9MC41LCB5PTAuNSwgIyBhIGNlbnRlcmVkIHZpZXdwb3J0CiMjICAgICAgICAgd2lkdGg9dW5pdChtaW4oMSxkaWZmKHhsaW0pL2RpZmYoeWxpbSkpLCAic25wYyIpLCAjIGFzcGVjdCByYXRpbyBwcmVzZXJ2ZWQKIyMgICAgICAgIGhlaWdodD11bml0KG1pbigxLGRpZmYoeWxpbSkvZGlmZih4bGltKSksICJzbnBjIiksCiMjICAgICAgICB4c2NhbGU9eGxpbSwgIyBjZi4geGxpbQojIyAgICAgICAgeXNjYWxlPXlsaW0gICMgY2YuIHlsaW0KIyMpKQojIyBub2xpbnQgZW5kCmdyaWQucmVjdCgwLjUsIDAuNSwgMSwgMSwgZ3AgPSBncGFyKGZpbGwgPSAiYmxhY2siKSkKbHMgPC0gZXhwYW5kLmdyaWQoeCA9IDA6MSwgeSA9IHNlcSgwLCAxLCAxIC8gbnggLyAyKSAtIDEgLyBueCAvIDIgLyAyKQpncmlkLnBvbHlsaW5lKGxzJHgsIGxzJHksIGlkID0gZ2wobnJvdyhscykgLyAyLCAyKSwKICAgICAgICAgICAgICBncCA9IGdwYXIoY29sID0gImdyZXkiLCBsd2QgPSBsd2QpKQpscyA8LSBleHBhbmQuZ3JpZCh5ID0gMCA6IDEsIHggPSBzZXEoMCwgMSwgMSAvIG55IC8gMikgLSAxIC8gbnkgLyAyIC8gMikKZ3JpZC5wb2x5bGluZShscyR4LCBscyR5LCBpZCA9IGdsKG5yb3cobHMpIC8gMiwgMiksCiAgICAgICAgICAgICAgZ3AgPSBncGFyKGNvbCA9ICJncmV5IiwgbHdkID0gbHdkKSkKbHMgPC0gZXhwYW5kLmdyaWQoeCA9IHNlcSgwLCAxLCAxIC8gbnggLyAyKSAtIDEgLyBueCAvIDIgLyAyLAogICAgICAgICAgICAgICAgICB5ID0gc2VxKDAsIDEsIDEgLyBueSAvIDIpIC0gMSAvIG55IC8gMiAvIDIpCmdyaWQuY2lyY2xlKGxzJHgsIGxzJHksIHIgPSBjciwgZ3AgPSBncGFyKGNvbCA9IE5BLCBmaWxsID0gIndoaXRlIikpCmBgYAoKW0hlcm1hbm4gZ3JpZAppbGx1c2lvbl0oaHR0cHM6Ly9wc3ljaG9sb2d5LmZhbmRvbS5jb20vd2lraS9HcmlkX2lsbHVzaW9uI0hlcm1hbm5fZ3JpZF9pbGx1c2lvbik6CiJHaG9zdC1saWtlIiBncmV5IGJsb2JzIGF0IHRoZSBpbnRlcnNlY3Rpb25zIG9mIHdoaXRlIGxpbmVzLgoKYGBge3IsIGVjaG8gPSBGQUxTRX0KZ3JpZC5uZXdwYWdlKCkKZ3JpZC5yZWN0KDAuNSwgMC41LCAxLCAxLCBncCA9IGdwYXIoZmlsbCA9ICJibGFjayIpKQpncCA8LSBncGFyKGNvbCA9ICJ3aGl0ZSIsIGx3ZCA9IDIwKQpscyA8LSBleHBhbmQuZ3JpZCh4ID0gMCA6IDEsIHkgPSBzZXEoMCwgMSwgbGVuID0gbngpKQpncmlkLnBvbHlsaW5lKGxzJHgsIGxzJHksIGlkID0gZ2wobnJvdyhscykgLyAyLCAyKSwgZ3AgPSBncCkKZ3JpZC5wb2x5bGluZShscyR5LCBscyR4LCBpZCA9IGdsKG5yb3cobHMpIC8gMiwgMiksIGdwID0gZ3ApCmBgYAoKR3JpZCBpbGx1c2lvbiBpbiBhIGNhcnRvZ3JhbToKCjwhLS0gIyMgbm9saW50IHN0YXJ0OiBsaW5lX2xlbmd0aCAtLT4KPCEtLSBodHRwczovL3R3aXR0ZXIuY29tL2hyYnJtc3RyL3N0YXR1cy8xMjgxNjgxNDY5NDc2NDEzNDQ3IC0tPgpgYGB7ciwgZWNobyA9IEZBTFNFLCBtZXNzYWdlID0gRkFMU0UsIHdhcm5pbmcgPSBGQUxTRSwgb3V0LndpZHRoID0gIjYwJSJ9CmxpYnJhcnkoZ2d0ZXh0KQpsaWJyYXJ5KHN0YXRlYmlucykKbGlicmFyeShocmJydGhlbWVzKQpsaWJyYXJ5KHRpZHl2ZXJzZSkKCiMjIGpzb25saXRlOjpmcm9tSlNPTigKIyMgICAiaHR0cHM6Ly9zdGF0aWMwMS5ueXQuY29tL25ld3NncmFwaGljcy8yMDIwLzA2LzAyL3Rlc3RpbmctZGFzaGJvYXJkLzM2YTdmOWY3MWZiNjI3MTA3OGRmMzAxYjgwMTIxODUwMTZjODUxY2Yvc3RhdGVzLmpzb24iCiMjICkgLT4gY3ZkZgpjdmRmIDwtIGpzb25saXRlOjpmcm9tSlNPTihXTE5LKCJueXQtc3RhdGVzLTIwMjAtMDYtMDIuanNvbiIpKQoKY3ZkZiB8PgogIHVubmVzdChkYXRhKSB8PgogIG11dGF0ZShkYXRlID0gYXMuRGF0ZShkYXRlKSkgfD4KICBmaWx0ZXIoZGF0ZSA9PSBtYXgoZGF0ZSkpIHw+CiAgbXV0YXRlKHRlc3RfcGN0ID0gdGVzdHNfbmV3IC8gZXN0X3Rlc3RzX25lZWRlZCkgfD4KICBzZWxlY3QocG9zdGFsLCB0ZXN0X3BjdCkgfD4KICBtdXRhdGUoCiAgICBzdGF0dXMgPSBjYXNlX3doZW4oCiAgICAgIHRlc3RfcGN0ID4gMS4yIH4gImFib3ZlIiwKICAgICAgdGVzdF9wY3QgPCAwLjggfiAiYmVsb3ciLAogICAgICBUUlVFIH4gIm5lYXIiCiAgICApCiAgKSB8PgogIGdncGxvdCgpICsKICBnZW9tX3N0YXRlYmlucygKICAgIGFlcyhzdGF0ZSA9IHBvc3RhbCwgZmlsbCA9IHN0YXR1cykKICApICsKICBjb29yZF9maXhlZCgpICsKICBzY2FsZV9maWxsX21hbnVhbCgKICAgIG5hbWUgPSBOVUxMLAogICAgdmFsdWVzID0gYygKICAgICAgIm5lYXIiID0gIiNmZWJmODIiLAogICAgICAiYmVsb3ciID0gIiNjNzYxNWIiLAogICAgICAiYWJvdmUiID0gIiNiYWNmYTIiCiAgICApCiAgKSArCiAgbGFicygKICAgIHRpdGxlID0gIklzIFlvdXIgU3RhdGUgRG9pbmcgRW5vdWdoIENvcm9uYXZpcnVzIFRlc3Rpbmc/IiwKICAgIHN1YnRpdGxlID0gIjxzcGFuIHN0eWxlPSdjb2xvcjojYmFjZmEyO2ZvbnQtc2l6ZToxNXB0Oyc+KioxMioqPC9zcGFuPiBzdGF0ZXMgbWVldCB0aGUgdGVzdGluZyB0YXJnZXQ7PGJyPiA8c3BhbiBzdHlsZT0nY29sb3I6I2ZlYmY4Mjtmb250LXNpemU6MTVwdDsnPioqNSoqPC9zcGFuPiBhcmUgbmVhciB0aGUgdGFyZ2V0OyA8c3BhbiBzdHlsZT0nY29sb3I6I2M3NjE1Yjtmb250LXNpemU6MTVwdDsnPioqMzQqKjwvc3Bhbj4gYXJlIGJlbG93IHRoZSB0YXJnZXQ7IiwKICAgIGNhcHRpb24gPSAiRGF0YSBzb3VyY2U6IE5ZVGltZXMgPHd3dy5ueXRpbWVzLmNvbS9pbnRlcmFjdGl2ZS8yMDIwL3VzL2Nvcm9uYXZpcnVzLXRlc3RpbmcuaHRtbD4iCiAgKSArCiAgdGhlbWVfaXBzdW1fZXMoZ3JpZCA9ICIiLCBwbG90X3RpdGxlX3NpemUgPSAxNSwgY2FwdGlvbl9zaXplID0gNykgKwogIHRoZW1lKAogICAgcGxvdC50aXRsZSA9IGVsZW1lbnRfdGV4dChoanVzdCA9IDAuNSksCiAgICBwbG90LnN1YnRpdGxlID0gZWxlbWVudF9tYXJrZG93bihmYW1pbHkgPSBmb250X2VzLCBmYWNlID0gInBsYWluIiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGhqdXN0ID0gMC41LCBzaXplID0gMTApCiAgKSArCiAgdGhlbWUoYXhpcy50ZXh0LnggPSBlbGVtZW50X2JsYW5rKCksIGF4aXMudGV4dC55ID0gZWxlbWVudF9ibGFuaygpKSArCiAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gIm5vbmUiLCBwbG90Lm1hcmdpbiA9IHVuaXQoYygxLCAxLCAxLCAxLjUpLCAiY20iKSkKYGBgCjwhLS0gIyMgbm9saW50IGVuZCAtLT4KCkEgY2FzZSB3aGVyZSB0aGVyZSBhcmUgbW9yZSBkb3RzIHRoYW4gd2UgY2FuIHNlZSBhdCBvbmNlOgo8IS0taHR0cHM6Ly90d2l0dGVyLmNvbS90ZXNsYXBoeC9zdGF0dXMvMTM3MzQzNjcyNjcyNzc0NTUzNz9zPTExIC0tPgoKYGBge3IgZWNobyA9IEZBTFNFLCBvdXQud2lkdGggPSAiNDAlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJkaXNhcHBlYXJpbmctZG90cy5qcGVnIikpCmBgYAoKUmVkIGZyb20gYmxhY2sgYW5kIHdoaXRlOgoKPCEtLSBodHRwczovL3R3aXR0ZXIuY29tL0FraXlvc2hpS2l0YW9rYS9zdGF0dXMvMTU5MTc4NDg5NzI4MjQ3ODA4MCAtLT4KCmBgYHtyIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjUwJSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygicmVkX2Zyb21fYmxhY2tfYW5kX3doaXRlLmpwZWciKSkKYGBgCgpTb21lIGlsbHVzaW9ucyBpbiBwaWN0dXJlczoKCjwhLS0gaHR0cHM6Ly90d2l0dGVyLmNvbS9ueHRob21wc29uL3N0YXR1cy8xMzU3MTQ3OTY4MzI4MTE4MjcyP3M9MTEgLS0+CmBgYHtyIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjUwJSIsIGZpZy5jYXAgPSAiQSBtYW4gcnVubmluZyBpbnRvIHRoZSBzbm93In0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJtYW5faW5fc25vdy5qcGVnIikpCmBgYAo8IS0tIGh0dHBzOi8vdHdpdHRlci5jb20vbWFya3lzdW1tL3N0YXR1cy8xMzM3NzI1ODUxNzk5MDU2Mzg2P3M9MTEgLS0+CmBgYHtyIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjUwJSIsIGZpZy5jYXAgPSAiT25jZSB5b3Ugc2VlIENvb2tpZSBNb25zdGVyLCB5b3UgY2Fu4oCZdCB1bnNlZSBpdCJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiY29va2llLW1vbnN0ZXIuanBlZyIpKQpgYGAKCkEgbGFyZ2UgY29sbGVjdGlvbiBvZiBvcHRpY2FsIGlsbHVzaW9ucyBpcyBhdmFpbGFibGUgYXQKPGh0dHBzOi8vbWljaGFlbGJhY2guZGUvb3QvaW5kZXguaHRtbD4uCgo8IS0tCk90aGVyIGxpbmtzIHRvIG9wdGljYWwgaWxsdXNpb25zIGNhbiBiZSBmb3VuZCBbaGVyZV0oaHR0cHM6Ly9vbmxpbmVtYXN0ZXJzLm9oaW8uZWR1L21hc3RlcnMtaGVhbHRoLWFkbWluaXN0cmF0aW9uL2hlYWx0aC1icmFpbi1nYW1lcy1vcHRpY2FsLWlsbHVzaW9ucy8pLgotLT4KCgojIyMgTW90aW9uCgpgYGB7ciBjaHVuay1sYWJlbCwgZmlnLndpZHRoID0gMTAsIGZpZy5zaG93PSdhbmltYXRlJywgZmZtcGVnLmZvcm1hdD0nZ2lmJywgZGV2PSdqcGVnJywgaW50ZXJ2YWwgPSAwLjEsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpuIDwtIDUwCnggPC0gMiAqICgxIDogbikKeSA8LSByZXAoMiwgbikKbGltIDwtIGMobWluKHgpICsgMC4xICogKG1heCh4KSAtIG1pbih4KSksIG1heCh4KSAtIDAuMSAqIChtYXgoeCkgLSBtaW4oeCkpKQp2IDwtIFRSVUUKZm9yIChpIGluIDEgOiAyKSB7CiAgICBwbG90KHggKyB2LCB5LCB4bGltID0gbGltKQogICAgdiA8LSAhIHYKICAgIFN5cy5zbGVlcCgwLjEpCn0KYGBgCgo8IS0tIE1vcmUgbW90aW9uIGlsbHVzaW9uczoKICBodHRwczovL3R3aXR0ZXIuY29tL0FubmVMYXVyZV9EYXZpZC9zdGF0dXMvMTUxMzU5Nzk5MDY2OTI3MTA0NQogIGh0dHBzOi8vdHdpdHRlci5jb20vamFnYXJpa2luL3N0YXR1cy8xNTMxMTE1NzMxMjIzMzM5MDA4Ci0tPgoKYGBge3IsIGluY2x1ZGUgPSBGQUxTRX0KZ2lmX2ZpbGUgPC0gIjNkc2NhdHRlcl9wZXJjZXAuZ2lmIgppZiAoISBmaWxlLmV4aXN0cyhJTUcoZ2lmX2ZpbGUpKSkgewogICAgbGlicmFyeShyZ2wpCiAgICBkIDwtIGRhdGEuZnJhbWUoeCA9IHJub3JtKDEwMDApLCB5ID0gcm5vcm0oMTAwMCksIHogPSBybm9ybSgxMDAwKSkKICAgIHBvaW50czNkKGQpCiAgICBwYXIzZChGT1YgPSAxKSAgIyMgcmVtb3ZlcyBwZXJzcGVjdGl2ZSBkaXN0b3J0aW9uCiAgICBtb3ZpZTNkKAogICAgICAgIG1vdmllID0gc3ViKCJcXC4uKiIsICIiLCBnaWZfZmlsZSksCiAgICAgICAgc3BpbjNkKGF4aXMgPSBjKDAsIDAsIDEpLCBycG0gPSAyMCksCiAgICAgICAgZHVyYXRpb24gPSAzLAogICAgICAgIHR5cGUgPSAiZ2lmIiwKICAgICAgICBkaXIgPSBJTUcoIiIpLAogICAgICAgIGNsZWFuID0gVFJVRQogICAgKQogICAgIyMgcmUtc2F2ZSBzbyBpdCBsb29wcyBpbmRlZmluaXRlbHkKICAgIGltZyA8LSBtYWdpY2s6OmltYWdlX3JlYWQoSU1HKGdpZl9maWxlKSkKICAgIG1hZ2ljazo6aW1hZ2Vfd3JpdGUoaW1nLCBwYXRoID0gSU1HKGdpZl9maWxlKSkKfQpgYGAKYGBge3IsIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjc1JSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiM2RzY2F0dGVyX3BlcmNlcC5naWYiKSkKYGBgCgpJbWFnZXMgY29udGFpbiBubyBpbmZvcm1hdGlvbiBhYm91dCB0aGUgZGlyZWN0aW9uIG9mIHRoZSByb3RhdGlvbi4KCllvdXIgbWluZCBwaWNrcyBhIGRpcmVjdGlvbi4KCmBgYHtyLCBpbmNsdWRlID0gRkFMU0V9CmtuaXRyOjprbml0X2hvb2tzJHNldCh3ZWJnbCA9IHJnbDo6aG9va193ZWJnbCkKb3B0aW9ucyhyZ2wudXNlTlVMTCA9IFRSVUUpCmBgYApgYGB7ciwgd2ViZ2wgPSBUUlVFLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShyZ2wpCmQgPC0gZGF0YS5mcmFtZSh4ID0gcm5vcm0oMTAwMCksIHkgPSBybm9ybSgxMDAwKSwgeiA9IHJub3JtKDEwMDApKQpwb2ludHMzZChkKQpwYXIzZChGT1YgPSAxKSAgIyMgcmVtb3ZlcyBwZXJzcGVjdGl2ZSBkaXN0b3J0aW9uCmlmIChpbnRlcmFjdGl2ZSgpKQogICAgcGxheTNkKHNwaW4zZChheGlzID0gYygwLCAwLCAxKSwgcnBtID0gMzApLCBkdXJhdGlvbiA9IDIwKQpgYGAKCkludGVyYWN0aXZlIHJvdGF0aW9uIGNhbiBoZWxwLgoKRGVwdGggY3VlaW5nIGFuZCBwZXJzcGVjdGl2ZSBjYW4gYWxzbyBoZWxwLgoKCiMjIyBQb3BvdXQgYW5kIERpc3RyYWN0b3JzCgpXaGVyZSBpcyB0aGUgcmVkIGRvdDoKCmBgYHtyLCBlY2hvID0gRkFMU0V9CnRobSA8LSB0aGVtZV9jbGFzc2ljKCkKdGhtIDwtIGxpc3QodGhlbWVfdm9pZCgpLAogICAgICAgICAgICB0aGVtZShwYW5lbC5ib3JkZXIgPSBlbGVtZW50X3JlY3QoZmlsbCA9IE5BLCBjb2xvciA9ICJncmV5MjAiKSksCiAgICAgICAgICAgIGd1aWRlcyhjb2xvciA9ICJub25lIiwgc2hhcGUgPSAibm9uZSIpLAogICAgICAgICAgICBzY2FsZV9zaGFwZV9tYW51YWwodmFsdWVzID0gYyhBID0gMTYsIEIgPSAxNSkpLAogICAgICAgICAgICBjb29yZF9lcXVhbCgpLCB4bGltKGMoMCwgMSkpLCB5bGltKGMoMCwgMSkpKQoKcHRzIDwtIGZ1bmN0aW9uKG4sIHZlcnNpb24sIHN6ID0gMykgewogICAgaWR4IDwtIHNlcV9sZW4obikKICAgIGlmICh2ZXJzaW9uID09IDEpIHsKICAgICAgICB2MSA8LSBpZmVsc2UoaWR4ID09IDEsICJBIiwgIkIiKQogICAgICAgIHYyIDwtICJBIgogICAgfQogICAgZWxzZSBpZiAodmVyc2lvbiA9PSAyKSB7CiAgICAgICAgdjEgPC0gIkEiCiAgICAgICAgdjIgPC0gaWZlbHNlKGlkeCA9PSAxLCAiQSIsICJCIikKICAgIH0KICAgIGVsc2UgaWYgKHZlcnNpb24gPT0gMykgewogICAgICAgIHYxIDwtIGlmZWxzZShpZHggPT0gMSB8IGlkeCA+IChuIC8gMiksICJBIiwgIkIiKQogICAgICAgIHYyIDwtIGlmZWxzZShpZHggPD0gKG4gLyAyKSwgIkEiLCAiQiIpCiAgICB9CiAgICBkIDwtIGRhdGEuZnJhbWUoeCA9IHJ1bmlmKG4pLCB5ID0gcnVuaWYobiksIHYxID0gdjEsIHYyID0gdjIpCiAgICBnZ3Bsb3QoZCwgYWVzKHgsIHksIGNvbG9yID0gdjEsIHNoYXBlID0gdjIpKSArIGdlb21fcG9pbnQoc2l6ZSA9IHN6KSArIHRobQp9CgpwMSA8LSBwdHMoMTAsIDEpCnAyIDwtIHB0cygxMDAsIDEpCnAzIDwtIHB0cygxMCwgMikKcDQgPC0gcHRzKDEwMCwgMikKcDUgPC0gcHRzKDEwLCAzKQpwNiA8LSBwdHMoMTAwLCAzKQpgYGAKCmBgYHtyLCBlY2hvID0gRkFMU0UsIGRwaSA9IDMwMCwgb3V0LndpZHRoID0gIjYwJSJ9CmdyaWQuYXJyYW5nZShwMSwgcDIsIG5yb3cgPSAxKQpgYGAKClNoYXBlIG9ubHk6CgpgYGB7ciwgZWNobyA9IEZBTFNFLCBkcGkgPSAzMDAsIG91dC53aWR0aCA9ICI2MCUifQpncmlkLmFycmFuZ2UocDMsIHA0LCBucm93ID0gMSkKYGBgCgpTaGFwZXMgYW5kIGNvbG9yczoKCmBgYHtyLCBlY2hvID0gRkFMU0UsIGRwaSA9IDMwMCwgb3V0LndpZHRoID0gIjYwJSJ9CmdyaWQuYXJyYW5nZShwNSwgcDYsIG5yb3cgPSAxKQpgYGAKCgojIyBJdGVtcywgQXR0cmlidXRlcywgTWFya3MsIGFuZCBDaGFubmVscwoKVG8gZXZhbHVhdGUgb3IgZGVzaWduIGEgdmlzdWFsaXphdGlvbiBpdCBpcyB1c2VmdWwgdG8gaGF2ZSBzb21lIHRlcm1zCmZvciB0aGUgY29tcG9uZW50cy4KClNldmVyYWwgc2Nob29scyBoYXZlIGRldmVsb3BlZCBkaWZmZXJlbnQgYnV0IHNpbWlsYXIgc2V0cyBvZiB0ZXJtcy4KClNvbWUgUmVmZXJlbmNlczoKCiogQmVydGluLCBKLiAoMTk2NyksIF9UaGUgU2VtaW9sb2d5IG9mIEdyYXBoaWNzXy4KKiBDbGV2ZWxhbmQsIFcuIFMuICgxOTg4KSwgX1RoZSBFbGVtZW50cyBvZiBHcmFwaGluZyBEYXRhXy4KKiBDbGV2ZWxhbmQsIFcuIFMuICgxOTkzKSwgX1Zpc3VhbGl6aW5nIERhdGFfLgoqIEZldywgUy4gKDIwMTIpLCBfU2hvdyBNZSB0aGUgTnVtYmVyczogRGVzaWduaW5nIFRhYmxlcyBhbmQgR3JhcGhzIHRvCiAgRW5saWdodGVuXywgMm5kIGVkLgoqIE11bnpuZXIsIFQuICgyMDE0KSwgX1Zpc3VhbGl6YXRpb24gQW5hbHlzaXMgYW5kIERlc2lnbl8KKiBXYXJlLCBDLiAoMjAxMiksIF9JbmZvcm1hdGlvbiBWaXN1YWxpemF0aW9uOiBQZXJjZXB0aW9uIGZvciBEZXNpZ25fLCAzcmQgZWQuCiogV2lsa2luc29uLCBMLiAoMjAwNSksIF9UaGUgR3JhbW1hciBvZiBHcmFwaGljc18sIDJuZCBlZC4KCk11bnpuZXIgdXNlcyB0aGUgdGVybWlub2xvZ3kgb2YgX2l0ZW1zXywgX2F0dHJpYnV0ZXNfLCBfbGlua3NfLApfbWFya3NfLCBhbmQgX2NoYW5uZWxzXzoKCiogX0l0ZW1zXyBhcmUgdGhlIGJhc2ljIHVuaXRzIG9uIHdoaWNoIGRhdGEgaXMgY29sbGVjdGVkOiB0aGUgZW50aXRpZXMKICByZXByZXNlbnRlZCBieSB0aGUgcm93cyBpbiBhIF90aWR5XyBkYXRhIGZyYW1lLgoKKiBfQXR0cmlidXRlc18gYXJlIHRoZSBudW1lcmljYWwgb3IgY2F0ZWdvcmljYWwgZmVhdHVyZXMgb2YgdGhlIGRhdGEKICBpdGVtcyB3ZSB3YW50IHRvIHJlcHJlc2VudDsgdGhlIHZhcmlhYmxlcyBpbiBhIHRpZHkgZGF0YSBmcmFtZS4KCiogX0xpbmtzXyBhcmUgcmVsYXRpb25zIGFtb25nIGl0ZW1zOiBlLmcuIG1vbnRocyB3aXRoaW4gYSB5ZWFyLCBvcgogIGNvdW50cmllcyB3aXRoaW4gYSBjb250aW5lbnQuCgoqIF9NYXJrc18gYXJlIHRoZSBnZW9tZXRyaWMgZW50aXRpZXMgdXNlZCB0byByZXByZXNlbnQgaXRlbXM6IHBvaW50cywKICBsaW5lcywgYXJlYXMuIFRoZXNlIGNvcnJlc3BvbmQgdG8gdGhlIHNpbXBsZSBgZ2VvbWAgb2JqZWN0cyBpbgogIGBnZ3Bsb3RgLgoKKiBfVmlzdWFsIGNoYW5uZWxzXyBhcmUgZmVhdHVyZXMgb2YgbWFya3MgdGhhdCBjYW4gYmUgdXNlZCB0byByZWZsZWN0CiAgdmFsdWVzIG9mIGF0dHJpYnV0ZXMuCgpDaGFubmVscyBjb3JyZXNwb25kIGFwcHJveGltYXRlbHkgdG8gYWVzdGhldGljcyBpbiBgZ2dwbG90YCBidXQgYXJlCm1vcmUgZm9jdXNlZCBvbiB0aGUgdmlzdWFsIGFzcGVjdDoKCiogQW4gYHhgIGFlc3RoZXRpYyB0aGF0IGlzIHRyYW5zZm9ybWVkIHRvIHBvbGFyIGNvb3JkaW5hdGVzIGlzIGEKICBkaWZmZXJlbnQgY2hhbm5lbCB0aGFuIGFuIGB4YCBhZXN0aGV0aWMgcmVwcmVzZW50aW5nIGEgcG9zaXRpb24gb24gYQogIHN0YW5kYXJkIGxpbmVhciBzY2FsZS4KCkNoYW5uZWxzIGFyZSB1c2VkIHRvIF9lbmNvZGVfIGF0dHJpYnV0ZXMgKF9hZXN0aGV0aWMgbWFwcGluZ3NfKS4KCkEgc2luZ2xlIGF0dHJpYnV0ZSBjYW4gYmUgZW5jb2RlZCBpbiBzZXZlcmFsIGNoYW5uZWxzLgoKKiBUaGlzIG1ha2VzIHRoZSBhdHRyaWJ1dGUgZWFzaWVyIHRvIHBlcmNlaXZlLgoKKiBCdXQgaXQgYWxzbyB1c2VzIHVwIGF2YWlsYWJsZSBjaGFubmVscy4KClNvbWUgY2hhbm5lbHMgYXJlIHdlbGwgc3VpdGVkIHRvIGVuY29kZSBxdWFudGl0YXRpdmUgb3Igb3JkZXJlZAp2YWx1ZXM7IHRoZXkgYXJlIF9xdWFudGl0YXRpdmVseSBwZXJjZWl2ZWRfLgoKT3RoZXJzIGFyZSBvbmx5IHN1aXRlZCBmb3Igbm9taW5hbCB2YWx1ZXMuCgpBIHVzZWZ1bCBjbGFzc2lmaWNhdGlvbiwgYWRhcHRlZCBmcm9tIEZldygyMDEyKToKCnwgVHlwZSAgICAgfCAgQ2hhbm5lbCAgICB8ICBRdWFudGl0YXRpdmVseSBQZXJjZWl2ZWQ/ICB8Cnw6LS0tLS0tLS0tfDotLS0tLS0tLS0tLS18Oi0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLSB8CnwgRm9ybSAgICAgfCBMZW5ndGggICAgICB8IFllcyAgICAgICAgICAgICAgICAgICAgICAgICB8CnwgICAgICAgICAgfCBXaWR0aCAgICAgICB8IFllcywgYnV0IGxpbWl0ZWQgICAgICAgICAgICB8CnwgICAgICAgICAgfCBPcmllbnRhdGlvbiB8IE5vICAgICAgICAgICAgICAgICAgICAgICAgICB8CnwgICAgICAgICAgfCBTaXplICAgICAgICB8IFllcywgYnV0IGxpbWl0ZWQgICAgICAgICAgICB8CnwgICAgICAgICAgfCBTaGFwZSAgICAgICB8IE5vICAgICAgICAgICAgICAgICAgICAgICAgICB8CnwgQ29sb3IgICAgfCBIdWUgICAgICAgICB8IE5vICAgICAgICAgICAgICAgICAgICAgICAgICB8CnwgICAgICAgICAgfCBJbnRlbnNpdHkgICB8IFllcywgYnV0IGxpbWl0ZWQgICAgICAgICAgICB8CnwgUG9zaXRpb24gfCAyRCBwb3NpdGlvbiB8IFllcyAgICAgICAgICAgICAgICAgICAgICAgICB8CgpNdW56bmVyIHVzZXMgdGhlIHRlcm1zIF9tYWduaXR1ZGUgY2hhbm5lbHNfIGFuZCBfaWRlbnRpdHkgY2hhbm5lbHNfLgoKSWRlYWxseSwKCiogbnVtZXJpYyBhbmQgb3JkZXJlZCBhdHRyaWJ1dGVzIHNob3VsZCBiZSByZXByZXNlbnRlZCBieSBxdWFudGl0YXRpdmVseQogIHBlcmNlaXZlZCBjaGFubmVsczsKCiogdW5vcmRlcmVkIGNhdGVnb3JpY2FsIGF0dHJpYnV0ZXMgc2hvdWxkIGJlIHJlcHJlc2VudGVkIGJ5CiAgbm9uLXF1YW50aXRhdGl2ZSBjaGFubmVscy4KCkEgdXNlZnVsIHByaW5jaXBsZTogVGhlIG1vc3QgaW1wb3J0YW50IGF0dHJpYnV0ZXMgc2hvdWxkIGJlIG1hcHBlZCB0bwp0aGUgbW9zdCBlZmZlY3RpdmUgY2hhbm5lbHMuCgoKIyMgQ2hhbm5lbCBFZmZlY3RpdmVuZXNzCgpTb21lIHF1ZXN0aW9ucyBhYm91dCBjaGFubmVsczoKCiogV2hhdCBraW5kIGFuZCBob3cgbXVjaCBpbmZvcm1hdGlvbiBjYW4gYSBjaGFubmVsIGVuY29kZT8KCiogQXJlIHNvbWUgY2hhbm5lbHMgYmV0dGVyIHRoYW4gb3RoZXJzPwoKKiBDYW4gY2hhbm5lbHMgYmUgdXNlZCBpbmRlcGVuZGVudGx5LCBvciBkbyB0aGV5IGludGVyZmVyZT8KClNvbWUgY3JpdGVyaWEgZm9yIGV2YWx1YXRpbmcgY2hhbm5lbHM6CgoqIEFjY3VyYWN5OiBIb3cgd2VsbCBjYW4gYSB2aWV3ZXIgZGVjb2RlIHRoZSBpbmZvcm1hdGlvbiBpbiB0aGUgY2hhbm5lbD8KCiogRGlzY3JpbWluYWJpbGl0eTogSG93IGVhc2lseSBjYW4gZGlmZmVyZW5jZXMgYmV0d2VlbiBhdHRyaWJ1dGUKICBsZXZlbHMgYmUgcGVyY2VpdmVkPwoKKiBTZXBhcmFiaWxpdHk6IENhbiBjaGFubmVscyBiZSB1c2VkIGluZGVwZW5kZW50bHkgb3IgaXMgdGhlcmUKICBpbnRlcmZlcmVuY2U/CgoqIFBvcG91dDogY2FuIGEgY2hhbm5lbCBwcm92aWRlIF9wb3BvdXRfIHdoZXJlIGEgZGlmZmVyZW5jZSBpcyBwZXJjZWl2ZWQKICBwcmVhdHRlbnRpdmVseT8KCiogR3JvdXBpbmc6IGNhbiBhIGNoYW5uZWwgc2hvdyBwZXJjZXB0dWFsIGdyb3VwaW5nIG9mIGl0ZW1zPwoKCiMjIyBDaGFubmVsIEFjY3VyYWN5CgpTdGV2ZW5zICgxOTU3KSBhcmd1ZXMgdGhhdCBhY2N1cmFjeSBvZiBtYWduaXR1ZGUgY2hhbm5lbHMgY2FuIGJlCmRlc2NyaWJlZCBieSBhIHBvd2VyIGxhdzoKCiQkIFx0ZXh0e3BlcmNlaXZlZCBzZW5zYXRpb259ID0gKFx0ZXh0e3BoeXNpY2FsIGludGVuc2l0eX0pXlxnYW1tYSAkJAoKRXhwZXJpbWVudHMgYnkgU3RldmVucyBzdWdnZXN0IHRoZXNlIHZhbHVlcyBmb3Igc29tZSB2aXN1YWwgY2hhbm5lbHM6CgpgYGB7ciwgZWNobyA9IEZBTFNFLCBmaWcuaGVpZ2h0ID0gNH0KbiA8LSAxMDAKeCA8LSBzZXEoMCwgNSwgbGVuID0gbikKZ2FtbWEgPC0gYygwLjUsIDAuNjcsIDAuNywgMSwgMS43KQpjaGFuIDwtIGMoIkJyaWdodG5lc3MiLCAiRGVwdGgiLCAiQXJlYSIsICJMZW5ndGgiLCAiU3RhdHVyYXRpb24iKQpsYWJlbCA8LSBzcHJpbnRmKCIlcyAoJS4yZikiLCBjaGFuLCBnYW1tYSkKbmMgPC0gbGVuZ3RoKGdhbW1hKQpkIDwtIGRhdGEuZnJhbWUoSW50ZW5zaXR5ID0gcmVwKHgsIG5jKSwKICAgICAgICAgICAgICAgIGdhbW1hID0gcmVwKGdhbW1hLCBlYWNoID0gbiksCiAgICAgICAgICAgICAgICBsYWJlbCA9IHJlcChsYWJlbCwgZWFjaCA9IG4pKQpwIDwtIGdncGxvdChkLCBhZXMoeCA9IEludGVuc2l0eSwgeSA9IEludGVuc2l0eSBeIGdhbW1hKSkgKwogICAgZ2VvbV9saW5lKGFlcyhncm91cCA9IGdhbW1hLCBjb2xvciA9IGxhYmVsKSwKICAgICAgICAgICAgICBsaW5ld2lkdGggPSAxLjUpICsgeWxpbShjKDAsIDUpKSArCiAgICBsYWJzKHggPSAiUGhpc2ljYWwgSW50ZW5zaXR5IiwgeSA9ICJQZXJjZWl2ZWQgU2Vuc2F0aW9uIikgKwogICAgdGhlbWVfbWluaW1hbCgpICsKICAgIHRoZW1lKHBhbmVsLmJvcmRlciA9IGVsZW1lbnRfcmVjdChmaWxsID0gTkEsIGNvbG9yID0gImdyZXkyMCIpKQpzdXBwcmVzc1dhcm5pbmdzKHByaW50KHApKQpgYGAKCltPdGhlcnMgaGF2ZSByYWlzZWQgY29uY2VybnNdKGh0dHBzOi8vZW4ud2lraXBlZGlhLm9yZy93aWtpL1N0ZXZlbnMlMjdzX3Bvd2VyX2xhdykKYWJvdXQgdGhlIHZhbGlkaXR5IG9mIHRoZXNlIGZpbmRpbmdzLgoKPCEtLQoKIyMjIEFzcGVjdCBSYXRpbwpgYGB7ciwgZXZhbCA9IEZBTFNFfQpyaXZlciA8LSBzY2FuKCJodHRwczovL3d3dy5zdGF0LnVpb3dhLmVkdS9+bHVrZS9kYXRhL3JpdmVyLmRhdCIpCnBsb3Qocml2ZXIpCmBgYAoKKioqKiBtaXNsZWFkaW5nIGV4YW1wbGUgZnJvbSBIVzIgYXMgc2xvcGVzCi0tPgoKYGBge3IsIGVjaG8gPSBGQUxTRSwgZXZhbCA9IEZBTFNFfQojIyBDb2xvciB3aGVlbCBmb3IgaHVlOgpuIDwtIDcyCnBpZShyZXAoMSwgbiksIGNvbCA9IGhzdigoMSA6IG4pIC8gbiwgMSwgMSksIGJvcmRlciA9IE5BLCBsYWJlbHMgPSBOQSkKYGBgCgpgYGB7ciwgZWNobyA9IEZBTFNFLCBldmFsID0gRkFMU0V9CiMjIFZhbHVlIGFuZCBzYXR1cmF0aW9uCnBsb3QoMCwgdHlwZSA9ICJuIiwgYXNwID0gMSwKICAgICB4bGltID0gYygwLCAxKSwgeWxpbSA9IGMoMCwgMSksCiAgICAgYXhlcyA9IEZBTFNFLCB4bGFiID0gInZhbHVlL2xpZ2h0bmVzcyIsIHlsYWIgPSAic2F0dXJhdGlvbiIsCiAgICAgbWFyID0gYygwLCAwLCAwLCAwKSkKCm4gPC0gMzIKeCA8LSBzZXEoMCwgMSwgbGVuZ3RoLm91dCA9IG4pWy1uXQpodWUgPC0gcmdiMmhzdihjb2wycmdiKCJibHVlIikpW1siaCIsIDFdXQoKZGVseCA8LSBtZWFuKGRpZmYoeCkpCmRlbHkgPC0gMSAvIG4KZm9yIChpIGluIDEgOiBuKQogICAgcmVjdCh4LCBkZWx5ICogKGkgLSAxKSwgeCArIGRlbHgsIGRlbHkgKiBpLAogICAgICAgICBjb2wgPSBoc3YoaHVlLCBkZWx5ICogaSwgeCArIGRlbHgpLCBib3JkZXIgPSBOQSkKYGBgCgpgYGB7ciwgZWNobyA9IEZBTFNFLCBldmFsID0gRkFMU0V9CiMjIEFub3RoZXIgYXBwcm9hY2gKb3BhciA8LSBwYXIobWZyb3cgPSBjKDIsIDEpKQpuIDwtIDY0CnggPC0gc2VxKDAsIDEsIGxlbmd0aC5vdXQgPSBuKVstbl0KaHVlIDwtIHJnYjJoc3YoY29sMnJnYigiYmx1ZSIpKVtbImgiLCAxXV0KZGVseCA8LSBtZWFuKGRpZmYoeCkpCgpwbG90KDAsIHR5cGUgPSAibiIsIHhsaW0gPSBjKDAsIDEpLCB5bGltID0gYygwLCAxKSwKICAgICBheGVzID0gRkFMU0UsIHhsYWIgPSAiIiwgeWxhYiA9ICIiLCBtYXIgPSBjKDAsIDAsIDAsIDApKQpyZWN0KHgsIDAuMiwgeCArIGRlbHgsIDAuNywgY29sID0gaHN2KGh1ZSwgeCwgMSksIGJvcmRlciA9IE5BKQp0aXRsZSgiU2F0dXJhdGlvbiIpCgpwbG90KDAsIHR5cGUgPSAibiIsIHhsaW0gPSBjKDAsIDEpLCB5bGltID0gYygwLCAxKSwKICAgICBheGVzID0gRkFMU0UsIHhsYWIgPSAiIiwgeWxhYiA9ICIiLCBtYXIgPSBjKDAsIDAsIDAsIDApKQpyZWN0KHgsIDAuMiwgeCArIGRlbHgsIDAuNywgY29sID0gaHN2KGh1ZSwgMSwgeCksIGJvcmRlciA9IE5BKQp0aXRsZSgiVmFsdWUiKQoKcGFyKG9wYXIpCmBgYAoKQW5vdGhlciBhcHByb2FjaCBoYXMgdXNlZCBjb250cm9sbGVkIGV4cGVyaW1lbnRzIHRvIGFzc2VzcyBhY2N1cmFjeSBvZgp2YXJpb3VzIGNoYW5uZWxzIHVzZWQgaW4gdmlzdWFsaXphdGlvbnM6CgoqIFdpbGxpYW0gUy4gQ2xldmVsYW5kIGFuZCBSb2JlcnQgTWNHaWxsICgxOTg0KSwgIkdyYXBoaWNhbAogIFBlcmNlcHRpb246IFRoZW9yeSwgRXhwZXJpbWVudGF0aW9uLCBhbmQgQXBwbGljYXRpb24gdG8gdGhlCiAgRGV2ZWxvcG1lbnQgb2YgR3JhcGhpY2FsIE1ldGhvZHMsIiBfSm91cm5hbCBvZiB0aGUgQW1lcmljYW4KICBTdGF0aXN0aWNhbCBBc3NvY2lhdGlvbl8gNzksIDUzMeKAkzU1NC4KCiogV2lsbGlhbSBTLiBDbGV2ZWxhbmQgYW5kIFJvYmVydCBNY0dpbGwgKDE5ODcpLCAiR3JhcGhpY2FsCiAgUGVyY2VwdGlvbjogVGhlIFZpc3VhbCBEZWNvZGluZyBvZiBRdWFudGl0YXRpdmUgSW5mb3JtYXRpb24gb24KICBHcmFwaGljYWwgRGlzcGxheXMgb2YgRGF0YSIgX0pvdXJuYWwgb2YgdGhlIFJveWFsIFN0YXRpc3RpY2FsCiAgU29jaWV0eS4gU2VyaWVzIEFfLCAxOTItMjI5LgoKKiBKZWZmcmV5IEhlZXIgYW5kIE1pY2hhZWwgQm9zdG9jayAoMjAxMCkgIkNyb3dkc291cmNpbmcgR3JhcGhpY2FsCiAgUGVyY2VwdGlvbjogVXNpbmcgTWVjaGFuaWNhbCBUdXJrIHRvIEFzc2VzcyBWaXN1YWxpemF0aW9uIERlc2lnbiwiCiAgX1Byb2NlZWRpbmdzIG9mIHRoZSBTSUdDSElfLCAyMDMtMjEyLgoKTXVuem5lcidzIG9yZGVyaW5nIGJ5IGFjY3VyYWN5OgoKYGBge3IsIGVjaG8gPSBGQUxTRX0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJ0bW1jaGFubmVscy5qcGVnIikpCmBgYApUaGlzIG9yZGVyaW5nIGlzIHNvbWV0aW1lcyByZWZlcnJlZCB0byBhcyBhIF9wZXJjZXB0dWFsIGxhZGRlcl8uCgo8IS0tCk1hZ25pdHVkZSBDaGFubmVscyAoT3JkZXJlZCwgTnVtZXJpY2FsKSAgICBJZGVudGl0eSBDaGFubmVscyAoQ2F0ZWdvcmljYWwpCi0tLS0tLS0tLS0gICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAtLS0tLQpQb3NpdGlvbiBvbiBjb21tb24gc2NhbGUgICAgICAgICAgICAgICAgICAgU3BhdGlhbCBncm91cGluZwpQb3NpdGlvbiBvbiB1bmFsaWduZWQgc2NhbGUgICAgICAgICAgICAgICAgQ29sb3IgaHVlCkxlbmd0aCAoMUQgc2l6ZSkgICAgICAgICAgICAgICAgICAgICAgICAgICBTaGFwZQpUaWx0LCBhbmdsZQpBcmVhICgyRCBzaXplKQpEZXB0aCAoM0QgcG9zaXRpb24pCkNvbG9yIGx1bWluYW5jZSwgc2F0dXJhdGlvbgpDdXJ2YXR1cmUsIHZvbHVtZSAoM0Qgc2l6ZSkKLS0+CgpMaW5lIHdpZHRoIGlzIGFub3RoZXIgY2hhbm5lbDsgbm90IHN1cmUgdGhlcmUgaXMgYWdyZWVtZW50IG9uIGl0cwphY2N1cmFjeSwgYnV0IGl0IGlzIG5vdCBoaWdoLgoKCiMjIyBEaXNjcmltaW5hYmlsaXR5CgpNYW55IGNoYW5uZWxzLCBpbiBwYXJ0aWN1bGFyIGlkZW50aXR5IGNoYW5uZWxzLCBjYW4gb25seSBzdXBwb3J0IGEKbGltaXRlZCBudW1iZXIgb2YgZGlzY3JpbWluYWJsZSBsZXZlbHMuCgoqIExpbmUgd2lkdGggaXMgb25lIG9mIHRoZSBtb3N0IGxpbWl0ZWQgd2l0aCBwZXJoYXBzIDMgbGV2ZWxzLgoKKiBVc2luZyBtb3JlIHRoYW4gNSBvciA2IGNvbG9yIGh1ZXMgaXMgbm90IHJlY29tbWVuZGVkLgoKKiBTaW1pbGFybHksIHVzaW5nIG1vcmUgdGhhbiA1IG9yIDYgc3ltYm9sIHNoYXBlcyBjYW4gY3JlYXRlIGRpZmZpY3VsdGllcy4KCklmIHRoZSBudW1iZXIgb2YgbGV2ZWxzIHRoYXQgY2FuIGJlIHJlcHJlc2VudGVkIGJ5IGEgY2hhbm5lbCBpcwpzbWFsbGVyIHRoYW4gdGhlIG51bWJlciBvZiBhdHRyaWJ1dGUgbGV2ZWxzIHRoZW4gc29tZSBmb3JtIG9mCm1lYW5pbmdmdWwgYWdncmVnYXRpb24gaXMgbmVlZGVkLgoKCiMjIyBTZXBhcmFiaWxpdHkKClNvbWUgZW5jb2RpbmdzIGNhbiBiZSB1c2VkIGluZGVwZW5kZW50bHkgb2YgZWFjaCBvdGhlcjsgb3RoZXJzCmludGVyZmVyZSB3aXRoIGVhY2ggb3RoZXIgdG8gc29tZSBkZWdyZWUuCgo8IS0tICoqKiogc29tZXRoaW5nIGxpa2UgTXVuem5lciBGaWcgNS4xMCAtLT4KYGBge3IsIGVjaG8gPSBGQUxTRSwgb3V0LndpZHRoID0gIjU1JSJ9CmtuaXRyOjppbmNsdWRlX2dyYXBoaWNzKElNRygiVE1maWc1LjEwLmpwZyIpKQpgYGAKCiogVmVydGljYWwgYW4gaG9yaXpvbnRhbCBwb3NpdGlvbiBjYW4gYmUgdXNlZCBpbmRlcGVuZGVudGx5LgoKKiBDb2xvciAoaHVlKSBhbmQgcG9zaXRpb24gY2FuIGJlIHVzZWQgaW5kZXBlbmRlbnRseQoKKiBTaXplIGFuZCBodWUgaW50ZXJmZXJlIHNvbWV3aGF0OyBodWUgaXMgaGFyZGVyIHRvIHBlcmNlaXZlIG9uCiAgc21hbGxlciBvYmplY3RzLgoKKiBXaWR0aCBhbmQgaGVpZ2h0IGRvIG5vdCBmdW5jdGlvbiB3ZWxsIGluZGVwZW5kZW50bHk7IHRoZSByZXN1bHQgaXMKICBwZXJjZWl2ZWQgcHJpbWFyaWx5IGFzIHNoYXBlLgoKKiBFbmNvZGluZyB0d28gZGlmZmVyZW50IHZhbHVlcyBpbiB0aGUgcmVkIGFuZCBncmVlbiBjaGFubmVscyBhcyBhIGh1ZQogIGRvZXMgbm90IHdvcmsgYXQgYWxsLgoKCiMjIyBQb3BvdXQKCk1hbnkgY2hhbm5lbHMgc3VwcG9ydCBfdmlzdWFsIHBvcG91dF86IGhhdmluZyBvbmUgaXRlbSBvciBhIGZldyBpdGVtcwppbW1lZGlhdGVseSBzdGFuZCBvdXQgZnJvbSB0aGUgb3RoZXJzLgoKKiBDb2xvciAoaHVlIGFuZCBpbnRlbnNpdHkpIGRvIHRoaXMgd2VsbC4KCiogU2hhcGUgYW5kIHNpemUgY2FuIGFsc28gYmUgdXNlZCBlZmZlY3RpdmVseSB0byBjcmVhdGUgcG9wb3V0LgoKQW5ub3RhdGlvbiBjYW4gYWxzbyBiZSB1c2VkIHRvIGNyZWF0ZSBwb3BvdXQuCgoKIyMjIEdyb3VwaW5nCgpQZXJjZXB0dWFsIGdyb3VwaW5nIGNhbiBiZSBhY2hpZXZlZCBpbiBzZXZlcmFsIHdheXM6CgoqIFVzaW5nIGFuIGlkZW50aXR5IGNoYW5uZWwgdG8gdG8gcmVwcmVzZW50IGl0ZW1zIGFzIGEgZ3JvdXAuCgoqIFVzaW5nIF9saW5rIG1hcmtzXy4KCiogQnkgX2VuY2xvc3VyZV8uCgoqIEJ5IHNwYXRpYWwgcHJveGltaXR5LgoKYGBge3IsIGVjaG8gPSBGQUxTRX0KZDEgPC0gZGF0YS5mcmFtZSh4ID0gYygxLCAyLCAzLCA0LCAxLCAyLCAzLCA0KSwKICAgICAgICAgICAgICAgICB5ID0gYygxLCAyLCAxLCAxLjUsIDYsIDUuNSwgNiwgNSksCiAgICAgICAgICAgICAgICAgdiA9IHJlcChjKCJBIiwgIkIiKSwgZWFjaCA9IDQpKQpwMSA8LSBnZ3Bsb3QoZDEsIGFlcyh4LCB5LCBjb2xvciA9IHYpKSArIGdlb21fcG9pbnQoc2l6ZSA9IDQpICsKICAgIHRoZW1lX3ZvaWQoKSArIGd1aWRlcyhjb2xvciA9ICJub25lIikgKwogICAgdGhlbWUocGFuZWwuYm9yZGVyID0gZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwgY29sb3IgPSAiZ3JleTIwIikpCmBgYAoKYGBge3IsIGVjaG8gPSBGQUxTRX0KZDEgPC0gZGF0YS5mcmFtZSh4ID0gYygxLCAyLCAzLCA0LCAxLCAyLCAzLCA0KSwKICAgICAgICAgICAgICAgICB5ID0gYygxLCAyLCAxLCAxLjUsIDYsIDUuNSwgNiwgNSksCiAgICAgICAgICAgICAgICAgdiA9IHJlcChjKCJBIiwgIkIiKSwgZWFjaCA9IDQpKQpwMiA8LSBnZ3Bsb3QoZDEsIGFlcyh4LCB5LCBjb2xvciA9IHYpKSArCiAgICBnZW9tX2xpbmUoYWVzKGdyb3VwID0gdiksIGNvbG9yID0gImJsYWNrIikgKwogICAgZ2VvbV9wb2ludChzaXplID0gNCkgKyB0aGVtZV92b2lkKCkgKyBndWlkZXMoY29sb3IgPSAibm9uZSIpICsKICAgIHRoZW1lKHBhbmVsLmJvcmRlciA9IGVsZW1lbnRfcmVjdChmaWxsID0gTkEsIGNvbG9yID0gImdyZXkyMCIpKQpgYGAKCmBgYHtyLCBlY2hvID0gRkFMU0V9CmQzIDwtIGRhdGEuZnJhbWUoeCA9IGMoMSwgMSwgMywgMyksCiAgICAgICAgICAgICAgICAgeSA9IGMoMSwgLTEsIDEsIC0xKSwKICAgICAgICAgICAgICAgICBzID0gYyg1LCAxMCwgMTAsIDUpKQpkMyRpIDwtIGZhY3RvcihzZXFfYWxvbmcoZDMkeCkgJSUgMikKcDMgPC0gZ2dwbG90KGQzKSArCiAgICBhbm5vdGF0ZSgicmVjdCIsIHhtaW4gPSAwLjYsIHltaW4gPSAtMS41LCB4bWF4ID0gMS41LCB5bWF4ID0gMS41LAogICAgICAgICAgICAgZmlsbCA9ICJncmF5IikgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IHgsIHkgPSB5LCBzaXplID0gcywgY29sb3IgPSBpKSkgKwogICAgc2NhbGVfc2l6ZV9hcmVhKG1heF9zaXplID0gMTApICsKICAgIGd1aWRlcyhzaXplID0gIm5vbmUiLCBjb2xvciA9ICJub25lIikgKyB0aGVtZV92b2lkKCkgKwogICAgeGxpbShjKDAsIDQpKSArIHlsaW0oYygtMiwgMikpICsKICAgIHRoZW1lKHBhbmVsLmJvcmRlciA9IGVsZW1lbnRfcmVjdChmaWxsID0gTkEsIGNvbG9yID0gImdyZXkyMCIpKQpgYGAKCmBgYHtyLCBlY2hvID0gRkFMU0V9CmQ0IDwtIGRhdGEuZnJhbWUoeCA9IGMoMSwgMiwgMywgMTAsIDEwLCAxMiksCiAgICAgICAgICAgICAgICAgeSA9IGMoMSwgLTEsIDEsIDYsIDgsIDYpLAogICAgICAgICAgICAgICAgIHMgPSBjKDUsIDEwLCAxMCwgNSwgNSwgMTApKQpkNCRpIDwtIGZhY3RvcihzZXFfYWxvbmcoZDQkeCkgJSUgMikKcDQgPC0gZ2dwbG90KGQ0KSArIGdlb21fcG9pbnQoYWVzKHggPSB4LCB5ID0geSwgc2l6ZSA9IHMsIGNvbG9yID0gaSkpICsKICAgIHNjYWxlX3NpemVfYXJlYShtYXhfc2l6ZSA9IDE1KSArCiAgICBndWlkZXMoc2l6ZSA9ICJub25lIiwgY29sb3IgPSAibm9uZSIpICsgdGhlbWVfdm9pZCgpICsKICAgIHlsaW0oYygtMiwgOSkpICsgeGxpbShjKDAsIDEzKSkgKwogICAgdGhlbWUocGFuZWwuYm9yZGVyID0gZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwgY29sb3IgPSAiZ3JleTIwIikpCmBgYAoKYGBge3IsIGVjaG8gPSBGQUxTRX0KZ3JpZC5hcnJhbmdlKHAxLCBwMiwgcDMsIHA0LCBucm93ID0gMikKYGBgCgoKIyMgRXhwZXJpbWVudGFsIEV2aWRlbmNlCgoKIyMjIENsZXZlbGFuZC1NY0dpbGwKClRoZSAxOTg0IHBhcGVyIGlzIGF2YWlsYWJsZSBmcm9tCltKU1RPUl0oaHR0cHM6Ly93d3cuanN0b3Iub3JnL3N0YWJsZS8yMjg4NDAwKS4KClRoZSBwYXBlciBmb3JtdWxhdGVzIGEgdGhlb3J5IGZvciByYW5raW5nIF9FbGVtZW50YXJ5IFBlcmNlcHR1YWwKVGFza3NfOyB0aGVzZSBjb3JyZXNwb25kIHRvIGNoYW5uZWwgbWFwcGluZ3MuCgpTb21lIG9yZGVyaW5ncyB3ZXJlIGFkZHJlc3NlZCBieSBpbmZvcm1hbCBleHBlcmltZW50cyAob2J2aW91cyB0byB0aGUKYXV0aG9ycyBhdCBsZWFzdCkuCgpPdGhlcnMgd2VyZSBhc3Nlc3NlZCBieSBmb3JtYWwgZXhwZXJpbWVudHMgd2l0aCBhYm91dCA1MCBzdWJqZWN0cy4KCkV4cGVyaW1lbnRzIGZvY3VzZWQgb24gYWNjdXJhY3kgb2YgZGVjb2RpbmcsIHRob3VnaCB0aGlzIGlzIG5vdCB2aWV3ZWQKYXMgdGhlIHByaW1hcnkgcHVycG9zZSBvZiBhIGdyYXBoOgoKPiBPbmUgbXVzdCBiZSBjYXJlZnVsIG5vdCB0byBmYWxsIGludG8gYSBjb25jZXB0dWFsIHRyYXAgb2YgYWRvcHRpbmcKPiBhY2N1cmFjeSBhcyBhIGNyaXRlcmlvbi4gLi4uIFRoZSBwb3dlciBvZiBhIGdyYXBoIGlzIGl0cyBhYmlsaXR5IHRvCj4gZW5hYmxlIG9uZSB0byB0YWtlIGluIHRoZSBxdWFudGl0YXRpdmUgaW5mb3JtYXRpb24sIG9yZ2FuaXplIGl0LCBhbmQKPiBzZWUgcGF0dGVybnMgYW5kIHN0cnVjdHVyZSBub3QgcmVhZGlseSByZXZlYWxlZCBieSBvdGhlciBtZWFucyBvZgo+IHN0dWR5aW5nIHRoZSBkYXRhLgoKVGhlaXIgcHJlbWlzZToKCj4gQSBncmFwaGljYWwgZm9ybSB0aGF0IGludm9sdmVzIGVsZW1lbnRhcnkgcGVyY2VwdHVhbCB0YXNrcyB0aGF0IGxlYWQKPiB0byBtb3JlIGFjY3VyYXRlIGp1ZGdtZW50cyB0aGFuIGFub3RoZXIgZ3JhcGhpY2FsIGZvcm0gKHdpdGggdGhlCj4gc2FtZSBxdWFudGl0YXRpdmUgaW5mb3JtYXRpb24pIHdpbGwgcmVzdWx0IGluIGJldHRlciBvcmdhbml6YXRpb24KPiBhbmQgaW5jcmVhc2UgdGhlIGNoYW5jZXMgb2YgYSBjb3JyZWN0IHBlcmNlcHRpb24gb2YgcGF0dGVybnMgYW5kCj4gYmVoYXZpb3IuIgoKVGhlIHRhc2tzOiBGb3IgZWFjaCBzZXR0aW5nCgoqIElkZW50aWZ5IHdoaWNoIG9mIHR3byBtYXJrZWQgaXRlbXMgaXMgc21hbGxlci4KCiogRXN0aW1hdGUgdGhlIHBlcmNlbnRhZ2UgdGhlIHNtYWxsZXIgaXMgb2YgdGhlIGxhcmdlci4KCiFbXShgciBJTUcoIkNNMS5qcGciKWApCgohW10oYHIgSU1HKCJDTTIucG5nIilgKQoKUmVzdWx0czoKClBlcmNlbnQgbGFyZ2UgZXJyb3JzOgoKIVtdKGByIElNRygiQ01MRS5qcGciKWApCgpBYnNvbHV0ZSBlcnJvcjoKCiFbXShgciBJTUcoImNsZXZlbGFuZC1yZXN1bHRzLnBuZyIpYCkKCgojIyMgSGVlciBhbmQgQm9zdG9jawoKW0hlZXIgYW5kIEJvc3RvY2sKICAoMjAxMCldKGh0dHBzOi8vaWRsLnV3LmVkdS9wYXBlcnMvY3Jvd2Rzb3VyY2luZy1ncmFwaGljYWwtcGVyY2VwdGlvbikKc2V0IG91dCB0byByZXBsaWNhdGUgdGhlIENsZXZlbGFuZCBNY0dpbGwgZXhwZXJpbWVudCB1c2luZyBjcm93ZApzb3VyY2luZyB2aWEgW0FtYXpvbiBNZWNoYW5pY2FsIFR1cmtdKGh0dHBzOi8vd3d3Lm10dXJrLmNvbS8pCgpUaGV5IHVzZWQgdGhlIGZpdmUgcG9zaXRpb24gc3RpbXVsaSBmcm9tIENsZXZlbGFuZCBhbmQgTWNHaWxsIGFuZApzb21lIG5ldyBvbmVzOgoKIVtdKGByIElNRygiaGVlci1ib3N0b2NrLXRhc2tzLnBuZyIpYCkKCjUwIHN1YmplY3RzIHdlcmUgcmVjcnVpdGVkIGZvciBlYWNoIHRhc2suCgpSZXN1bHRzIHdlcmUgY29uc2lzdGVudCB3aXRoIENsZXZlbGFuZC1NY0dpbGwgcmVzdWx0czoKCiFbXShgciBJTUcoIkhCMS5qcGVnIilgKQoKVXNlIG9mIE1lY2hhbmljYWwgVHVyayB3YXMgZGVlbWVkIGEgc3VjY2Vzcy4KCgojIyMgUGllIENoYXJ0IEV4cGVyaW1lbnRzCgpbUGllIGNoYXJ0c10oaHR0cHM6Ly9lYWdlcmV5ZXMub3JnL3BpZS1jaGFydHMpIGFyZSBwb3B1bGFyIGJ1dApzb21ld2hhdCBjb250cm92ZXJzaWFsLgoKKiBQaWUgY2hhcnRzIGFyZSBpbmZlcmlvciBmb3IgY29tcGFyaXNvbnMgdG8gYmFyIGNoYXJ0cy4KCiogUGllIGNoYXJ0cyBhcmUgcXVpdGUgZ29vZCBhdCByZXByZXNlbnRpbmcgcGFydC13aG9sZSByZWxhdGlvbnNoaXBzLgoKKiBDbGV2ZWxhbmQgYW5kIE1jR2lsbCBzdWdnZXN0ZWQgcGllIGNoYXJ0cyBhcmUgcmVhZCBieSBhbmdsZS4KCiogW0tvc2FyYSBhbmQgU2thdV0oaHR0cHM6Ly9lYWdlcmV5ZXMub3JnL3BhcGVycy9hLXBhaXItb2YtcGllLWNoYXJ0LXBhcGVycykKICByZXBvcnQgZXhwZXJpbWVudHMgdGhhdCBzdWdnZXN0IHRoaXMgaXMgbm90IHRoZSBjYXNlLgoKKiBJZiBpdCB3ZXJlLAogIFtfZG9udXQgY2hhcnRzX10oaHR0cHM6Ly9kYXRhdml6Y2F0YWxvZ3VlLmNvbS9tZXRob2RzL2RvbnV0X2NoYXJ0Lmh0bWwpCiAgd291bGQgYmUgZXZlbiBsZXNzIGVmZmVjdGl2ZSwgYnV0IHRoZXkgc2VlbSB0byBiZSB2ZXJ5IGNvbXBhcmFibGUuCgoqIFtLb3NhcmEncyBibG9nXShodHRwczovL2VhZ2VyZXllcy5vcmcpIHByb3ZpZGVzIGEKICBbcmV2aWV3XShodHRwczovL2VhZ2VyZXllcy5vcmcvYmxvZy8yMDE2L2FuLWlsbHVzdHJhdGVkLXRvdXItb2YtdGhlLXBpZS1jaGFydC1zdHVkeS1yZXN1bHRzKQogICAgICBvZiBvdGhlciBwaWUgY2hhcnQgc3R1ZGllcy4KCgojIyBJbXByb3ZpbmcgU29tZSBDb21tb24gQ2hhcnRzCgpDbGV2ZWxhbmQgYW5kIE1jR2lsbCBzZXQgb3V0IHRvIHN1Z2dlc3QgaW1wcm92ZW1lbnRzIHRvIHNvbWUgY29tbW9uIGNoYXJ0cy4KVGhpcyBpcyBhIHNlbGVjdGlvbiBvZiB0aGVpciBleGFtcGxlcy4KCgojIyMgRG90IENoYXJ0cwoKQ2xldmVsYW5kIGFuZCBNY0dpbGwgdXNlIHRoZWlyIHBlcmNlcHR1YWwgbGFkZGVyIHRvIGFyZ3VlIHN0cm9uZ2x5IGZvcgp1c2luZyBkb3QgY2hhcnRzIGluIHBsYWNlIG9mIGJhciBjaGFydHMgYW5kIHBpZSBjaGFydHMuCgoKIyMjIFBsYXlmYWlyJ3MgQmFsYW5jZSBvZiBUcmFkZSBwbG90cwoKUGxheWZhaXIgcHJlc2VudGVkIGEgbnVtYmVyIG9mIHBsb3RzIHNob3dpbmcgaW1wb3J0cyBhbmQgZXhwb3J0cwpiZXR3ZWVuIEVuZ2xhbmQgYW5kIG90aGVyIG5hdGlvbnMuCgpBIHByaW1hcnkgZ29hbCB3YXMgdG8gc2hvdyB0aGUgYmFsYW5jZSBvZiB0cmFkZSwgdGhlIGRpZmZlcmVuY2UKYmV0d2VlbiBleHBvcnRzIGFuZCBpbXBvcnRzOgoKIVtdKGByIElNRygiUGxheWZhaXJfRXhwb3J0c19JbXBvcnRzLmpwZyIpYCkKCkFzc2Vzc2luZyB0aGUgZGlmZmVyZW5jZXMgZnJvbSBhIHBsb3Qgc2hvd2luZyBleHBvcnRzIGFuZCBpbXBvcnRzIGFzCnNlcGFyYXRlIGN1cnZlcyByZXF1aXJlcyBsZW5ndGgganVkZ21lbnRzLCB3aGljaCBhcmUgbGVzcyBhY2N1cmF0ZQp0aGFuIGNvbXBhcmlzb25zIHRvIGEgY29tbW9uIHN0YWxlLgoKPCEtLQpkYXRhOgpodHRwczovL3Jhdy5naXRodWJ1c2VyY29udGVudC5jb20vamVubnliYy9yLWdyYXBoLWNhdGFsb2cvbWFzdGVyL2ZpZ3VyZXMvZmlnMDItMTRfcGxheWZhaXItcy1iYWxhbmNlLW9mLXRyYWRlLWRhdGEvZmlnMDItMTRfcGxheWZhaXItcy1iYWxhbmNlLW9mLXRyYWRlLWRhdGEudHN2Ci0tPgoKYGBge3IsIGluY2x1ZGUgPSBGQUxTRX0KIyBub2xpbnQgc3RhcnQKaWYgKCEgZmlsZS5leGlzdHMoInBsYXlmYWlyLWJhbGFuY2Utb2YtdHJhZGUtZGF0YS50c3YiKSkKICAgIGRvd25sb2FkLmZpbGUoImh0dHA6Ly93d3cuc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9wbGF5ZmFpci1iYWxhbmNlLW9mLXRyYWRlLWRhdGEudHN2IiwKICAgICAgICAgICAgICAgICAgInBsYXlmYWlyLWJhbGFuY2Utb2YtdHJhZGUtZGF0YS50c3YiKQojIG5vbGludCBlbmQKYGBgCgpgYGB7ciwgZWNobyA9IEZBTFNFfQpwaW1leCA8LSByZWFkLmRlbGltKCJwbGF5ZmFpci1iYWxhbmNlLW9mLXRyYWRlLWRhdGEudHN2IikKcHAxIDwtIG11dGF0ZShwaW1leCwgZGlmZmVyZW5jZSA9IE5VTEwpIHw+CiAgICBwaXZvdF9sb25nZXIoLXllYXIsIG5hbWVzX3RvID0gIndoaWNoIiwgdmFsdWVzX3RvID0gInRyYWRlIikgfD4KICAgIGdncGxvdChhZXMoeCA9IHllYXIsIHkgPSB0cmFkZSwgZ3JvdXAgPSB3aGljaCwgY29sb3IgPSB3aGljaCkpICsKICAgIGdlb21fbGluZSgpICsKICAgIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZShwYW5lbC5ib3JkZXIgPSBlbGVtZW50X3JlY3QoZmlsbCA9IE5BLCBjb2xvciA9ICJncmV5MjAiKSkKcHAxCmBgYAoKUGxvdHRpbmcgdGhlIGRpZmZlcmVuY2UgbWFrZXMgdGhlIGJhbGFuY2Ugb2YgdHJhZGUgbXVjaCBlYXNpZXIgdG8gYXNzZXNzOgoKYGBge3IsIGVjaG8gPSBGQUxTRX0KcHAyIDwtIGdncGxvdChwaW1leCkgKyBnZW9tX2xpbmUoYWVzKHggPSB5ZWFyLCB5ID0gaW1wb3J0cyAtIGV4cG9ydHMpKSArCiAgICB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUocGFuZWwuYm9yZGVyID0gZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwgY29sb3IgPSAiZ3JleTIwIikpCnBwMgpgYGAKCkFuIF9lbnNlbWJsZSBwbG90XyBzaG93aW5nIGJvdGggdmlld3MgbWF5IGFsc28gaGVscC4KCmBgYHtyLCBlY2hvID0gRkFMU0UsIGZpZy5oZWlnaHQgPSA2fQpsaWJyYXJ5KHBhdGNod29yaykKcHAxIC8gcHAyCmBgYAoKCiMjIyBGcmFtZWQgVW5hbGlnbmVkIEJhcnMKCkl0IGlzIGRpZmZpY3VsdCB0byBjb21wYXJlIGxlbmd0aHMgb2YgdW5hbGlnbmVkIHJlY3RhbmdsZXMgd2hlbiB0aGUKbGVuZ3RocyBhcmUgY2xvc2UuCgpgYGB7ciwgZWNobyA9IEZBTFNFfQpoMSA8LSA3LjQKaDIgPC0gNi43CmhiIDwtIDEwCm9mZiA8LSAzCnAxIDwtIGdncGxvdCgpICsKICAgIGdlb21fcmVjdChhZXMoeG1pbiA9IDAsIHltaW4gPSAwLCB4bWF4ID0gMSwgeW1heCA9IGgxKSwKICAgICAgICAgICAgICBmaWxsID0gbXV0ZWQoImJsdWUiKSkgKwogICAgZ2VvbV9yZWN0KGFlcyh4bWluID0gMiwgeW1pbiA9IG9mZiwgeG1heCA9IDMsIHltYXggPSBvZmYgKyBoMiksCiAgICAgICAgICAgICAgZmlsbCA9IG11dGVkKCJibHVlIikpICsKICAgIHRoZW1lX3ZvaWQoKSArCiAgICB5bGltKGMoLTEsIG9mZiArIGhiICsgMSkpICsgeGxpbShjKC0yLCA1KSkKcDEKYGBgCgpBZGRpbmcgYSBmcmFtZSBtb3ZlcyB0aGUgdGFzayB1cCB0aGUgcGVyY2VwdHVhbCBsYWRkZXIgdG8gYW4gdW5hbGlnbmVkCmNvbXBhcmlzb24gYWdhaW5zdCBhIGNvbW1vbiBzY2FsZS4KCmBgYHtyLCBlY2hvID0gRkFMU0V9CnAxICsgZ2VvbV9yZWN0KGFlcyh4bWluID0gMCwgeW1pbiA9IDAsIHhtYXggPSAxLCB5bWF4ID0gaGIpLAogICAgICAgICAgICAgICBmaWxsID0gTkEsIGNvbG9yID0gImJsYWNrIikgKwogICAgZ2VvbV9yZWN0KGFlcyh4bWluID0gMiwgeW1pbiA9IG9mZiwgeG1heCA9IDMsIHltYXggPSBvZmYgKyBoYiksCiAgICAgICAgICAgICAgY29sb3IgPSAiYmxhY2siLCBmaWxsID0gTkEpCmBgYAoKQ29tcGFyaW5nIHRvIGEgY29tbW9uIHNjYWxlIGlzIHN0aWxsIHRoZSBtb3N0IGVmZmVjdGl2ZSBhcHByb2FjaDoKCmBgYHtyLCBlY2hvID0gRkFMU0V9CmdncGxvdCgpICsKICAgIGdlb21fcmVjdChhZXMoeG1pbiA9IDAsIHltaW4gPSAwLCB4bWF4ID0gMSwgeW1heCA9IGgxKSwKICAgICAgICAgICAgICBmaWxsID0gbXV0ZWQoImJsdWUiKSkgKwogICAgZ2VvbV9yZWN0KGFlcyh4bWluID0gMiwgeW1pbiA9IDAsIHhtYXggPSAzLCB5bWF4ID0gaDIpLAogICAgICAgICAgICAgIGZpbGwgPSBtdXRlZCgiYmx1ZSIpKSArIHRoZW1lX3ZvaWQoKSArCiAgICB5bGltKGMoLTEsIG9mZiArIGhiICsgMSkpICsgeGxpbShjKC0yLCA1KSkKYGBgCgpCdXQgdGhpcyBkb2VzIHN1Z2dlc3QgdGhhdCB1c2luZyB1bmFsaWduZWQgZnJhbWVkIHJlY3RhbmdsZXMgdG8gZW5jb2RlCmEgX3RoaXJkXyB2YXJpYWJsZSwgd2l0aCBwb3NpdGlvbiBlbmNvZGluZyB0aGUgdHdvIHByaW1hcnkgdmFyaWFibGVzCm1heSBiZSBlZmZlY3RpdmUuCgoKIyMjIEZyYW1lZCBSZWN0YW5nbGUgTWFwcwoKQSBfY2hvcm9wbGV0aCBtYXBfIGlzIGEgY29tbW9uIHdheSB0byBkZXBpY3QgYSBxdWFudGl0YXRpdmUgdmFyaWFibGUgaW4KYSBnZW9ncmFwaGljIGNvbnRleHQuCgpTaGFkaW5nIGlzIHF1aXRlIGxvdyBvbiB0aGUgcGVyY2VwdHVhbCBsYWRkZXIuCgpDbGV2ZWxhbmQgYW5kIE1jR2lsbCBzdWdnZXN0IHRoZSB1c2Ugb2YgZnJhbWVkIHJlY3RhbmdsZXMgcG9zaXRpb25lZApvbiB0aGUgbWFwIGFzIGFuIGFsdGVybmF0aXZlLgoKVGhpcyBkb2VzIG5vdCBzZWVtIHRvIGhhdmUgY2F1Z2h0IG9uIHNvIGZhciwgdGhvdWdoIHlvdSBkbyBzb21ldGltZXMKc2VlIHRoZSB1c2Ugb2Ygb3RoZXIgZ2x5cGhzLCBzdWNoIGFzIHBpZSBjaGFydHMuCgo8IS0tICFbXShodHRwOi8vbGg0LmdncGh0LmNvbS9fTGVuQ1pseXphMjAvVFI4eWFIbXN5ekkvQUFBQUFBQUFKUjgveVR2bDdhd2RreXMvdG1wMTQ4MTZfdGh1bWIxX3RodW1iMS5qcGc/aW1nbWF4PTgwMCkgLS0+CmBgYHtyLCBlY2hvID0gRkFMU0UsIG91dC53aWR0aCA9ICI5MCUifQprbml0cjo6aW5jbHVkZV9ncmFwaGljcyhJTUcoIkNNbWFwLmpwZyIpKQpgYGAKCgojIyBBbmFseXppbmcgYSBEZXNpZ24KCkdyYXBoIGxheW91dCBpbnZvbHZlcyBzZXZlcmFsIGxldmVsczoKCiogUHJpbWFyeSBkYXRhIHJlcHJlc2VudGF0aW9uCgogICogaXRlbXMsIGF0dHJpYnV0ZXMKICAqIG1hcmtzLCBjaGFubmVscwoKKiBTdXBwb3J0aW5nIGZlYXR1cmVzCgogICogdHJlbmQgbGluZXMsIHJlZmVyZW5jZSBsaW5lcywgYW5ub3RhdGlvbnMKICAqIGF4ZXMsIGxlZ2VuZHMKCkEgdXNlZnVsIHN0cnVjdHVyZSBmb3IgZGVzY3JpYmluZyB0aGUgcHJpbWFyeSBmZWF0dXJlczoKCiogV2hhdCBhcmUgdGhlIGRhdGEgaXRlbXM/CiogV2hhdCBhcmUgdGhlIGF0dHJpYnV0ZXM/CiogV2hhdCBtYXJrcyBhcmUgdXNlZD8KKiBXaGF0IGNoYW5uZWxzIGFyZSB1c2VkPwoqIFdoaWNoIGF0dHJpYnV0ZSBpcyBtYXRjaGVkIHRvIGNoYW5uZWwgMQoqIFdoaWNoIGF0dHJpYnV0ZSBpcyBtYXRjaGVkIHRvIGNoYW5uZWwgMgoqIC4uLgoKVXNlZnVsIHF1ZXN0aW9uczoKCiogQXJlIHRoZSBtb3N0IGltcG9ydGFudCBhdHRyaWJ1dGVzIG1hcHBlZCB0byB0aGUgc3Ryb25nZXN0IGNoYW5uZWxzPwoqIERvIHRoZSBtYXBwaW5ncyBkbyBhIGdvb2Qgam9iIG9mIGNvbnZleWluZyB0aGUgcHJpbWFyeSBtZXNzYWdlPwoqIElmIG5vdCwgY2FuIHRoZSBncmFwaCBiZSBpbXByb3ZlZCBieSBhZGp1c3RpbmcgdGhlIG1hcHBpbmdzPwoKCiMjIyBBIEdhcG1pbmRlciBQbG90CgpPbmUgb2YgdGhlIGZyYW1lcyBvZiBhIHBsb3QgZnJvbSB0aGUgW0dhcE1pbmRlcgpzaXRlXShodHRwczovL3d3dy5nYXBtaW5kZXIub3JnKToKCiFbXShgciBJTUcoImdhcG1pbmRlcjIucG5nIilgKQoKKiBJdGVtcyBhcmUgY291bnRyaWVzIChpbiBhIHBhcnRpY3VsYXIgeWVhcikKCiogQXR0cmlidXRlcyBpbiB0aGUgcGxvdDoKICAgICogbGlmZSBleHBlY3RhbmN5CiAgICAqIGluY29tZSBwZXIgcGVyc29uCiAgICAqIHBvcHVsYXRpb24KICAgICogY29udGluZW50CiAgICAqIGNvdW50cnkgbmFtZQogICAgKiB5ZWFyCgoqIE1hcmtzOiBwb2ludHMgKG9yIGJ1YmJsZXMpLgoKKiBDaGFubmVscyBhbmQgbWFwcGluZ3M6CiAgICAqIGhvcml6b250YWwgcG9zaXRpb24sIG1hcHBlZCB0byBsb2cgaW5jb21lCiAgICAqIHZlcnRpY2FsIHBvc2l0aW9uLCBtYXBwZWQgdG8gbGlmZSBleHBlY3RhbmN5CiAgICAqIGFyZWEsIG1hcHBlZCB0byBwb3B1bGF0aW9uCiAgICAqIGNvbG9yIChodWUpLCBtYXBwZWQgdG8gY29udGluZW50CiAgICAqIGludGVyYWN0aXZlOiBtb3VzZS1vdmVyLCBtYXBwZWQgdG8gY291bnRyeSBuYW1lCiAgICAqIGludGVyYWN0aXZlOiB0aW1lIChvciBmcmFtZSksIG1hcHBlZCB0byB5ZWFyCgpUaGUgYmFzaWMgcGxvdCBjYW4gYmUgY3JlYXRlZCB3aXRoIGBnZ3Bsb3RgIGFuZCBhZXN0aGV0aWMgbWFwcGluZ3M6CgpgYGB7ciBnYXBtaW5kZXItYmFzaWMsIGV2YWwgPSBGQUxTRX0KbGlicmFyeShnYXBtaW5kZXIpCmdtMjAwNyA8LSBmaWx0ZXIoZ2FwbWluZGVyLCB5ZWFyID09IDIwMDcpCmdncGxvdChnbTIwMDcpICsKICAgIGdlb21fcG9pbnQoYWVzKHggPSBnZHBQZXJjYXAsCiAgICAgICAgICAgICAgICAgICB5ID0gbGlmZUV4cCwKICAgICAgICAgICAgICAgICAgIHNpemUgPSBwb3AsCiAgICAgICAgICAgICAgICAgICBjb2xvciA9IGNvbnRpbmVudCkpICsKICAgIHNjYWxlX3hfbG9nMTAoKSArCiAgICB5bGltKGMoMjAsIDg1KSkKYGBgCmBgYHtyIGdhcG1pbmRlci1iYXNpYywgZWNobyA9IEZBTFNFfQpgYGAKClRoZSBkYXRhIGluIHRoZSBgZ2FwbWluZGVyYCBwYWNrYWdlIGRpZmZlciBzb21ld2hhdCBmcm9tIHRoZSBkYXRhIHVzZWQKYnkgdGhlIEdhcG1pbmRlciBzaXRlLCBidXQgb3ZlcmFsbCB0aGUgcGxvdCBkZXNpZ25zIGFyZSB2ZXJ5IGNsb3NlLgoKV2l0aCBzb21lIGFkanVzdG1lbnRzIHRoZSBiYXNpYyBwbG90IGNhbiBiZSBicm91Z2h0IGNsb3NlIHRvIHRoZQpHYXBtaW5kZXIgdmVyc2lvbiBpbiBhcHBlYXJhbmNlOgoKYGBge3IgZ2FwbWluZGVyLWZ1bGwsIGV2YWwgPSBGQUxTRX0KZ20yMDA3IDwtIGZpbHRlcihnYXBtaW5kZXIsIHllYXIgPT0gMjAwNykgfD4KICAgIGFycmFuZ2UoZGVzYyhwb3ApKSAjIyBzb3J0IHRvIGF2b2lkIG92ZXItcGxvdHRpbmcKZ2dwbG90KGdtMjAwNykgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IGdkcFBlcmNhcCwKICAgICAgICAgICAgICAgICAgIHkgPSBsaWZlRXhwLAogICAgICAgICAgICAgICAgICAgc2l6ZSA9IHBvcCwKICAgICAgICAgICAgICAgICAgIGZpbGwgPSBjb250aW5lbnQpLAogICAgICAgICAgICAgICBzaGFwZSA9IDIxKSArICMjIHRvIGFsbG93IHRoZSB1c2luZyBgZmlsbGAgYWVzdGhldGljCiAgICBzY2FsZV94X2xvZzEwKGxhYmVscyA9IGNvbW1hKSArCiAgICB5bGltKGMoMjAsIDg1KSkgKwogICAgc2NhbGVfc2l6ZV9hcmVhKG1heF9zaXplID0gMjAsCiAgICAgICAgICAgICAgICAgICAgbGFiZWxzID0gY29tbWEsCiAgICAgICAgICAgICAgICAgICAgYnJlYWtzID0gYygwLjI1ICogMTAgXiA5LCAwLjUgKiAxMCBeIDksIDEwIF4gOSkpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKHZhbHVlcyA9IGMoQWZyaWNhID0gImRlZXBza3libHVlIiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgQXNpYSA9ICJyZWQiLAogICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBBbWVyaWNhcyA9ICJncmVlbiIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIEV1cm9wZSA9ICJnb2xkIiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgT2NlYW5pYSA9ICJicm93biIpKSArCiAgICBsYWJzKHggPSAiSW5jb21lIiwgeSA9ICJMaWZlIGV4cGVjdGFuY3kiKSArCiAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxNikpICsKICAgIGd1aWRlcyhmaWxsID0gZ3VpZGVfbGVnZW5kKHRpdGxlID0gIkNvbnRpbmVudCIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICBvdmVycmlkZS5hZXMgPSBsaXN0KHNpemUgPSA1KSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIG9yZGVyID0gMSksCiAgICAgICAgICAgc2l6ZSA9IGd1aWRlX2xlZ2VuZCh0aXRsZSA9ICJQb3B1bGF0aW9uIiwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGxhYmVsLmhqdXN0ID0gMSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIG9yZGVyID0gMikpICsKICAgIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZShwYW5lbC5ib3JkZXIgPSBlbGVtZW50X3JlY3QoZmlsbCA9IE5BLCBjb2xvciA9ICJncmV5MjAiKSkKYGBgCmBgYHtyIGdhcG1pbmRlci1mdWxsLCBlY2hvID0gRkFMU0UsIGZpZy5oZWlnaHQgPSA2LCBmaWcud2lkdGggPSA4fQpgYGAKClNvbWUgbm90ZXM6CgoqIFVzaW5nIGxhcmdlciBidWJibGVzIG1ha2VzIHRoZSBwbG90IG1vcmUgZW5nYWdpbmcuCgoqIFVzaW5nIGxhcmdlciBidWJibGVzIG1ha2VzIGRpZmZlcmVuY2VzIGluIHBvcHVsYXRpb24gZWFzaWVyIHRvCiAgYXNzZXNzLCBidXQgbWFrZXMgdGhlIHN0cmVuZ3RoIG9mIHRoZSByZWxhdGlvbnNoaXAgYmV0d2VlbiBsaWZlCiAgZXhwZWN0YW5jeSBhbmQgaW5jb21lIGhhcmRlciB0byBhc3Nlc3MuCgoqIFVzaW5nIGxhcmdlciBidWJibGVzIGFsc28gaW5jcmVhc2VzIHRoZSByaXNrIG9mCiAgb3Zlci1wbG90dGluZy4gU29ydGluZyB0aGUgcm93cyBzbyBsYXJnZXIgYnViYmxlIGFyZSBkcmF3biBmaXJzdAogIGhlbHBzIHJlZHVjZSB0aGUgcmlzayBzb21ld2hhdC4KClRoZXNlIHBsb3RzIHNob3cgYSBmYWlybHkgc3Ryb25nIG1hcmdpbmFsIGFzc29jaWF0aW9uIGJldHdlZW4gbGlmZQpleHBlY3RhbmN5IGFuZCBpbmNvbWUuCgpUaGVyZSBkb2VzIG5vdCBzZWVtIHRvIGJlIGEgc3Ryb25nIGFzc29jaWF0aW9uIG9mIHBvcHVsYXRpb24gd2l0aCB0aGUKb3RoZXIgdHdvIHZhcmlhYmxlcywgYnV0IHRoZXNlIHBsb3RzIGFyZSBub3QgaWRlYWwgZm9yIHRoYXQgYXNzZXNzbWVudC4KClRvIGp1ZGdlIHRoZSBtYXJnaW5hbCBhc3NvY2lhdGlvbiBiZXR3ZWVuIGxpZmUgZXhwZWN0YW5jeSBhbmQKcG9wdWxhdGlvbiBzaXplIHdlIGNhbiBjaGFuZ2UgdGhlIGNoYW5uZWwgbWFwcGluZzoKCiogbWFwIHRoZSBob3Jpem9udGFsIGF4aXMgdG8gcG9wdWxhdGlvbjsKKiBtYXAgYXJlYSB0byBpbmNvbWUuCgpgYGB7ciBnYXBtaW5kZXItbGlmZXBvcCwgZXZhbCA9IEZBTFNFfQpnZ3Bsb3QoZmlsdGVyKGdhcG1pbmRlciwgeWVhciA9PSAyMDA3KSkgKwogICAgZ2VvbV9wb2ludChhZXMoeCA9IHBvcCwKICAgICAgICAgICAgICAgICAgIHkgPSBsaWZlRXhwLAogICAgICAgICAgICAgICAgICAgc2l6ZSA9IGdkcFBlcmNhcCkpICsKICAgIHNjYWxlX3hfbG9nMTAoKSArCiAgICB5bGltKGMoMjAsIDg1KSkgKwogICAgdGhlbWVfbWluaW1hbCgpICsKICAgIHRoZW1lKHBhbmVsLmJvcmRlciA9CiAgICAgICAgICAgICAgZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgY29sb3IgPSAiZ3JleTIwIikpCmBgYApgYGB7ciBnYXBtaW5kZXItbGlmZXBvcCwgZWNobyA9IEZBTFNFfQpgYGAKClRoaXMgY29uZmlybXMgdGhhdCB0aGVyZSBpcyB2ZXJ5IGxpdHRsZSBhc3NvY2lhdGlvbiBiZXR3ZWVuIGxpZmUKZXhwZWN0YW5jeSBhbmQgcG9wdWxhdGlvbi4KClRoZSBhc3NvY2lhdGlvbiBiZXR3ZWVuIGxpZmUgZXhwZWN0YW5jeSBhbmQgaW5jb21lIGlzIHN0aWxsIHZpc2libGUsCmJ1dCBpcyBlYXNpZXIgdG8gYXNzZXNzIHdoZW4gdGhlc2UgdHdvIHZhcmlhYmxlcyBhcmUgbWFwcGVkIHRvIDJECnBvc2l0aW9uLgoKCiMjIyBNaWNoZWxpbiBTdGFycwoKVGhpcyBpbWFnZSwgZnJvbSBhCltibG9nIHBvc3RdKGh0dHA6Ly9jcmVhdGVodG1sNW1hcC5jb20vaW50ZXJhY3RpdmUtbWFwLWJsb2cvaW50ZXJhY3RpdmUtYnViYmxlLWNoYXJ0LWNvdW50cmllcy1yZWNlaXZlLXRoZS1tb3N0LW1pY2hlbGluLXN0YXJzLWVhY2gteWVhci8pLApzaG93cyB0aGUgdG90YWwgbnVtYmVyIG9mIHN0YXJzIGZvciBkaWZmZXJlbnQgY291bnRyaWVzOgoKIVtdKGByIElNRygibWljaGVsaW4tc3RhcnMucG5nIilgKQoKKiBJdGVtczogQ291bnRyaWVzIChpbiBhIHBhcnRpY3VsYXIgeWVhcikKCiogQXR0cmlidXRlczoKICAgICogY291bnRyeSBuYW1lCiAgICAqIG51bWJlciBvZiBzdGFycwoKKiBNYXJrczogYnViYmxlcywgdGV4dAoKKiBDaGFubmVscyBhbmQgbWFwcGluZ3M6CiAgICAqIGJ1YmJsZSBjb2xvciwgbWFwcGVkIHRvIGNvdW50cnkKICAgICogYnViYmxlIGFyZWEsIG1hcHBlZCB0byBudW1iZXIgb2Ygc3RhcnMKICAgICogdGV4dCwgbWFwcGVkIHRvIGNvdW50cnkgbmFtZSAod2hlcmUgcG9zc2libGUpCiAgICAqIHRleHQsIG1hcHBlZCB0byBudW1iZXIgb2Ygc3RhcnMgKHdoZXJlIHBvc3NpYmxlKQoKPCEtLSBzZXBhcmF0ZSBuZXh0IGxpbmUgLS0+CgpPYnNlcnZhdGlvbnM6CgoqIE5vbmUgb2YgdGhlIGNoYW5uZWxzIGFyZSB2ZXJ5IHN0cm9uZy4KCiogVGhlIHN0cm9uZ2VzdCBjaGFubmVscywgMkQgcG9zaXRpb24sIGFyZSBub3QgdXNlZC4KCiogVGhlIG51bWJlciBvZiBjb2xvcnMgdXNlZCBpcyB0b28gaGlnaC4KCkEgc2ltcGxlIF9kb3QgcGxvdF8gd291bGQgY29udmV5IHRoZSBkaXN0cmlidXRpb24gYmV0dGVyLgoKQSBkb3QgcGxvdCB1c2luZyBbMjAxNyBkYXRhXShtaWNoZWxpbi5kYXQpIGZyb20gYW4KW2FydGljbGVdKGh0dHBzOi8vd3d3LnRlbGVncmFwaC5jby51ay90cmF2ZWwvbWFwcy1hbmQtZ3JhcGhpY3MvbWFwLW1pY2hlbGluLXN0YXItcmVzdGF1cmFudHMtY291bnRyaWVzLXdpdGgtdGhlLW1vc3QvKQppbiBUaGUgVGVsZWdyYXBoOgoKYGBge3J9Cm1pY2hlbGluIDwtIHJlYWQudGFibGUoV0xOSygibWljaGVsaW4uZGF0IiksCiAgICAgICAgICAgICAgICAgICAgICAgaGVhZCA9IFRSVUUpCm1pY2hlbGluIDwtIG11dGF0ZShtaWNoZWxpbiwKICAgICAgICAgICAgICAgICAgIHN0YXJzID0gb25lICsgMiAqIHR3byArIDMgKiB0aHJlZSwKICAgICAgICAgICAgICAgICAgIGNvdW50cnkgPSByZW9yZGVyKGNvdW50cnksIHN0YXJzKSkKZ2dwbG90KG1pY2hlbGluLCBhZXMoeCA9IHN0YXJzLCB5ID0gY291bnRyeSkpICsKICAgIGdlb21fcG9pbnQoKSArCiAgICBsYWJzKHggPSAiU3RhcnMiLCB5ID0gTlVMTCkgKwogICAgdGhlbWVfbWluaW1hbCgpICsKICAgIHRoZW1lKHRleHQgPSBlbGVtZW50X3RleHQoc2l6ZSA9IDE2KSkgKwogICAgdGhlbWUocGFuZWwuYm9yZGVyID0KICAgICAgICAgICAgICBlbGVtZW50X3JlY3QoZmlsbCA9IE5BLAogICAgICAgICAgICAgICAgICAgICAgICAgICBjb2xvciA9ICJncmV5MjAiKSkKYGBgCgpFdmVuIGlmIGEgYnViYmxlIHBsb3QgaXMgZGVzaXJlZCBmb3IgYWVzdGhldGljIHJlYXNvbnMsIHBvc2l0aW9uCmNvdWxkIGJlIHVzZWQgdG8KCiogZ3JvdXAgY291bnRyaWVzIGJ5IGNvbnRpbmVudDsKKiBzaG93IGNvdW50cmllcyBvbiBhIG1hcC4KCkEgcGxvdCBsaWtlIHRoZSBvcmlnaW5hbCBjYW4gYmUgY29uc3RydWN0ZWQgYnkKCiogY29tcHV0aW5nIGxvY2F0aW9ucyBmb3IgYSBzZXQgb2YgcGFja2VkIHNwaGVyZXMgd2l0aCBzcGVjaWZpZWQgcmFkaWk7CiogdXNpbmcgYGdlb21fcG9pbnRgIGFuZCBgZ2VvbV90ZXh0YC4KCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KIyMgY3JlYXRlIHJhbmRvbWx5IGxvY2F0ZWQgIHBhY2tlZCBzcGhlcmVzIHdpdGggc3BlY2lmaWVkIGFyZWFzCmxpYnJhcnkocGFja2NpcmNsZXMpCnNldC5zZWVkKDU0MzIxKQpwYWNraW5nIDwtIGNpcmNsZVByb2dyZXNzaXZlTGF5b3V0KG1pY2hlbGluJHN0YXJzKQoKIyMgbWVyZ2UgY2lyY2xlIGxvY2F0aW9ucyB3aXRoIHN0YXJ0cyBkYXRhCm1jaXJjIDwtIGJpbmRfY29scyhwYWNraW5nLCBtaWNoZWxpbikgfD4KICAgIG11dGF0ZShjb3VudHJ5ID0gZmFjdG9yKGNvdW50cnkpKSAjIyBjbGVhbiBvdXQgc3RyYXkgYXR0cmlidXRlcwoKIyMgY29tcHV0ZSBzb21lIGNvbG9ycyB0byB1c2UKbnIgPC0gbnJvdyhtY2lyYykKcGFsIDwtIGNvbG9yUmFtcFBhbGV0dGUoUkNvbG9yQnJld2VyOjpicmV3ZXIucGFsKDksICJTZXQxIikpCmNvbHMgPC0gc2FtcGxlKHBhbChuciksIG5yKQoKIyMgdGhlc2UgbmVlZCB0dW5pbmcgZm9yIHRoZSBzY3JlZW4gb3IgUiBtYXJrZG93bgpjc2l6ZSA8LSA0NQp0c2l6ZSA8LSAyLjUKCiMjIHRoZSBiYXNpYyBwbG90CiMjIHVzZXMgc2hhcGUgPSAxOSBhbmQgYGNvbG9yYCBhZXN0aGV0aWMKcCA8LSBnZ3Bsb3QobWNpcmMsIGFlcyh4ID0geCwgeSA9IHkpKSArCiAgICBnZW9tX3BvaW50KGFlcyhzaXplID0gcmFkaXVzIF4gMiwgY29sb3IgPSBjb3VudHJ5KSwgc2hhcGUgPSAxOSkgKwogICAgc2NhbGVfc2l6ZV9hcmVhKG1heF9zaXplID0gY3NpemUpICsKICAgIGdlb21fdGV4dChhZXMobGFiZWwgPSBwYXN0ZShjb3VudHJ5LCBzdGFycywgc2VwID0gIlxuIikpLAogICAgICAgICAgICAgIGRhdGEgPSBmaWx0ZXIobWNpcmMsIHN0YXJzID49IDEyMCksCiAgICAgICAgICAgICAgc2l6ZSA9IHRzaXplKSArCiAgICBjb29yZF9maXhlZCgpCgojIyBhZGp1c3RtZW50cwpwICsgZ3VpZGVzKHNpemUgPSAibm9uZSIpICsKICAgIHNjYWxlX2NvbG9yX21hbnVhbCh2YWx1ZXMgPSBjb2xzKSArCiAgICB4bGltKHdpdGgobWNpcmMsIHJhbmdlKHgpICsgYygtMSwgMSkgKiBtYXgocmFkaXVzKSkpICsKICAgIHlsaW0od2l0aChtY2lyYywgcmFuZ2UoeSkgKyBjKC0xLCAxKSAqIG1heChyYWRpdXMpKSkgKwogICAgdGhlbWVfdm9pZCgpCmBgYAoKQSBzb21ld2hhdCBtb3JlIHJvYnVzdCBhcHByb2FjaAoKICAqIGNyZWF0ZXMgdmVydGV4IGRhdGEgZm9yIHBvbHlnb24gYXBwcm94aW1hdGlvbnMgdG8gdGhlIGNpcmNsZXM7CiAgKiBtZXJnZXMgdGhlIHN0YXJzIGRhdGEgd2l0aCB0aGUgcG9seWdvbiBkYXRhOwogICogdXNlcyBgZ2VvbV9wb2x5Z29uYCBhbmQgYGdlb21fdGV4dGAuCgpUaGlzIGlzIHZlcnkgc2ltaWxhciB0byB0aGUgd2F5IHNpbXBsZSBfY2hvcm9wbGV0aCBtYXBzXyBhcmUgY3JlYXRlZC4KCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KIyMgY29tcHV0ZSBwb2x5Z29uIGFwcHJveGltYXRpb25zIHRvIHNwaGVyZXMKbWNpcmNwb2x5IDwtIGNpcmNsZUxheW91dFZlcnRpY2VzKG1jaXJjLCBpZGNvbCA9ICJjb3VudHJ5IiwgbnBvaW50cyA9IDEwMCkgfD4KICAgIHJlbmFtZShjb3VudHJ5ID0gaWQpCgojIyBtZXJnZSB0aGUgc3RhcnMgZGF0YSBpbnRvIHRoZSBwb2x5Z29uIGRhdGEKc3R0YWIgPC0gc2VsZWN0KG1pY2hlbGluLCBjb3VudHJ5LCBzdGFycykKbWNpcmNwb2x5IDwtIGxlZnRfam9pbihtY2lyY3BvbHksIHN0dGFiLCAiY291bnRyeSIpCgojIyBjcmVhdGUgdGhlIHBsb3QKZ2dwbG90KG1jaXJjcG9seSwgYWVzKHggPSB4LCB5ID0geSkpICsKICAgIGdlb21fcG9seWdvbihhZXMoZmlsbCA9IGNvdW50cnkpKSArCiAgICBnZW9tX3RleHQoYWVzKGxhYmVsID0gcGFzdGUoY291bnRyeSwgc3RhcnMsIHNlcCA9ICJcbiIpKSwKICAgICAgICAgICAgICBkYXRhID0gZmlsdGVyKG1jaXJjLCBzdGFycyA+PSAxMjApLAogICAgICAgICAgICAgIHNpemUgPSB0c2l6ZSkgKwogICAgY29vcmRfZml4ZWQoKSArCiAgICBzY2FsZV9maWxsX21hbnVhbCh2YWx1ZXMgPSBjb2xzKSArCiAgICB0aGVtZV92b2lkKCkKYGBgCgoKIyMgQXNwZWN0IFJhdGlvIGFuZCBQZXJjZXB0aW9uCgpUaGUgcml2ZXIgZmxvdyBkYXRhIHNob3dzIGhvdyBpbXBvcnRhbnQgYXNwZWN0IHJhdGlvIGNhbiBiZSB0byBvdXIKYWJpbGl0eSB0byBkZXRlY3QgcGF0dGVybnM6CgpgYGB7ciwgZWNobyA9IEZBTFNFfQpsaWJyYXJ5KGdyaWRFeHRyYSkKcml2ZXIgPC0gc2NhbigiaHR0cHM6Ly93d3cuc3RhdC51aW93YS5lZHUvfmx1a2UvZGF0YS9yaXZlci5kYXQiKQpyIDwtIGRhdGEuZnJhbWUoZmxvdyA9IHJpdmVyLCBtb250aCA9IHNlcV9hbG9uZyhyaXZlcikpCgpwMCA8LSBnZ3Bsb3QociwgYWVzKHggPSBtb250aCwgeSA9IGZsb3cpKSArCiAgICB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUocGFuZWwuYm9yZGVyID0gZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwgY29sb3IgPSAiZ3JleTIwIikpCnAxIDwtIHAwICsgZ2VvbV9wb2ludCgpCgpncmlkLmFycmFuZ2UocDEgKyBjb29yZF9maXhlZChyYXRpbyA9IDM1KSwKICAgICAgICAgICAgIHAxICsgY29vcmRfZml4ZWQocmF0aW8gPSA0KSwgaGVpZ2h0cyA9IGMoMywgMSkpCmBgYAoKVXNpbmcgYSBsaW5lIHBsb3QgdGhlIGJhc2ljIHBlcmlvZGljaXR5IGJlY29tZXMgYXBwYXJlbnQgZXZlbiBpbiB0aGUKZmlyc3QgYXNwZWN0IHJhdGlvLgoKYGBge3IsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwMiA8LSBwMCArIGdlb21fbGluZSgpCnAyICsgY29vcmRfZml4ZWQocmF0aW8gPSAzNSkKYGBgCgpCdXQgdGhlIHN0ZWVwZXIgaW5jcmVhc2Uvc2hhbGxvd2VyIGRlY3JlYXNlIG9mIG1vc3QgcGVyaW9kcyBpcyBlYXNpZXIKdG8gc2VlIGluIHRoZSBzZWNvbmQgYXNwZWN0IHJhdGlvOgoKYGBge3IsIGZpZy5oZWlnaHQgPSAyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KcDIgKyBjb29yZF9maXhlZChyYXRpbyA9IDQpCmBgYAoKVGhlIGFzcGVjdCByYXRpbyBhbHNvIGluZmx1ZW5jZXMgaW50ZXJwcmV0YXRpb24gb2YgcmVzdWx0cy4KClNvbWUgYWx0ZXJuYXRpdmUgdmlld3Mgb2YgKHN1c3BlY3QpIGRhdGEgb24gdGhlIG51bWJlciBvZiBwZW9wbGUgb24KZ292ZXJubWVudCBhc3Npc3RhbmNlIG92ZXIgYSB0aW1lIHBlcmlvZDoKCmBgYHtyLCBtZXNzYWdlID0gRkFMU0UsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpsaWJyYXJ5KHJlYWRyKQp3IDwtIHJlYWRfY3N2KFdMTksoImh3Mi13ZWxmYXJlLmNzdiIpKQp3IDwtIG11dGF0ZSh3LCBvbkFzc2lzdGFuY2UgPSBvbkFzc2lzdGFuY2UgLyAxMCBeIDYpCncgPC0gbXV0YXRlKHcsCiAgICAgICAgICAgIGRhdGUgPSBzZXEoYXMuRGF0ZSgiMjAwOS0wMS0wMSIpLCBieSA9ICJxdWFydGVyIiwgbGVuZ3RoLm91dCA9IDEwKSkKCnAwIDwtIGdncGxvdCh3LCBhZXMoeCA9IGRhdGUsIHkgPSBvbkFzc2lzdGFuY2UpKSArCiAgICB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUocGFuZWwuYm9yZGVyID0gZWxlbWVudF9yZWN0KGZpbGwgPSBOQSwgY29sb3IgPSAiZ3JleTIwIikpCgpwMSA8LSBwMCArIGdlb21fbGluZShhZXMoZ3JvdXAgPSAxKSkKCmdyaWQuYXJyYW5nZShwMSwgcDEgKyBjb29yZF9maXhlZChyYXRpbyA9IDgpLAogICAgICAgICAgICAgcDEgKyB5bGltKDAsIG1heCh3JG9uQXNzaXN0YW5jZSkpLAogICAgICAgICAgICAgcDAgKyBnZW9tX2NvbCh3aWR0aCA9IDQwKSwgbmNvbCA9IDIpCmBgYAoKU29tZSBub3RlczoKCiogQXV0b21hdGVkIGNob2ljZXMgb2YgYXhpcyBzY2FsaW5nIGNhbiBhZmZlY3QgdGhlIGFzcGVjdCByYXRpbyBvZgogIHRoZSBjb250ZW50IG9mIGEgcGxvdC4KCiogQSB6ZXJvIGJhc2UgbGluZSBzdXBwb3J0cyByYXRpbyBjb21wYXJpc29ucy4KCiogVGhlIHByZWF0dGVudGl2ZSByZXNwb25zZSB0byBiYXIgY2hhcnRzIGlzIGFsd2F5cyB0byBjb21wYXJlCiAgcmF0aW9zLCBzbyB1c2luZyBhIHplcm8gYmFzZSBsaW5lIGlzIGltcG9ydGFudC4KCiogVXNpbmcgYSBub24temVybyBiYXNlIGxpbmUgZm9yIGxpbmUgcGxvdHMgYW5kIHNjYXR0ZXIgcGxvdHMKICBlbmNvdXJhZ2VzIGludGVydmFsLCBvciBkaWZmZXJlbmNlLCBjb21wYXJpc29ucy4KCiogUmVzZWFyY2ggb24gdGhlIGVmZmVjdCBvZiBhc3BhY3QgcmF0aW8gb24gcGVyY2VwdGlvbiBoYXMgZm9jdXNlZAogIG9uIGFjY3VyYWN5IG9mIHNsb3BlIGNvbXBhcmlzb25zLgoKKiBUaGUgZ2VuZXJhbCBtZXNzYWdlIGlzIHRoYXQga2VlcGluZyBhd2F5IGZyb20gc2xvcGVzIHRoYXQgYXJlIHRvbwogIHN0ZWVwIG9yIHRvbyBzaGFsbG93IGlzIGJlc3QuCgoqIF9CYW5raW5nIHRvIDQ1IGRlZ3JlZXNfLCBvciBjaG9vc2luZyBhbiBhc3BlY3QgcmF0aW8gc28gdGhlIHNsb3BlCiAgbWFnbml0dWRlcyBhcmUgZGlzdHJpYnV0ZWQgYXJvdW5kIDQ1IGRlZ3JlZXMgaXMgb2Z0ZW4gcmVjb21tZW5kZWQuCgoqIFRoaXMgYWxzbyB0ZW5kcyB0byBiZSBhIHVzZWZ1bCAibmV1dHJhbCBncm91bmQiIHdoZW4gcG9saXRpY2FsCiAgaW1wbGljYXRpb25zIGFyZSBpbnZvbHZlZC4KClNvbWUgcmVmZXJlbmNlczoKCiogQSBbYmxvZyBwb3N0XShodHRwczovL2VhZ2VyZXllcy5vcmcvYmFzaWNzL2JhbmtpbmctNDUtZGVncmVlcykgYnkKICBSb2JlcnQgS29zYXJhLgoKKiBXaWxsaWFtIFMuIENsZXZlbGFuZCwgTWFyeWx5biBFLiBNY0dpbGwgYW5kIFJvYmVydCBNY0dpbGwgKDE5ODgpLAogICJUaGUgU2hhcGUgUGFyYW1ldGVyIG9mIGEgVHdvLVZhcmlhYmxlIEdyYXBoIiwgX0pvdXJuYWwgb2YgdGhlCiAgQW1lcmljYW4gU3RhdGlzdGljYWwgQXNzb2NpYXRpb25fCiAgKFtKU1RPUl0oaHR0cDovL3d3dy5qc3Rvci5vcmcvc3RhYmxlLzIyODg4NDM/c2VxPTEjcGFnZV9zY2FuX3RhYl9jb250ZW50cykpCgoqIEp1c3RpbiBUYWxib3QsIEpvaG4gR2VydGgsIFBhdCBIYW5yYWhhbiAoMjAxMiksICJBbiBFbXBpcmljYWwgTW9kZWwKICBvZiBTbG9wZSBSYXRpbyBDb21wYXJpc29ucyIsIF9JRUVFIFRyYW5zLiBWaXN1YWxpemF0aW9uICYKICBDb21wLiBHcmFwaGljcyAoUHJvYy4gSW5mb1ZpcylfCiAgKFtQREZdKGh0dHA6Ly92aXMuc3RhbmZvcmQuZWR1L2ZpbGVzLzIwMTItU2xvcGVDb21wYXJpc29uLUluZm9WaXMucGRmKSkKCjwhLS0KQ2hlY2sgdGhpcyBvdXQ6Cmh0dHA6Ly90aW1lbHlwb3J0Zm9saW8uZ2l0aHViLmlvL2J1aWxkaW5nd2lkZ2V0cy93ZWVrMTEvZXhhbXBsZV8wNy5odG1sCi0tPgoKPCEtLQpNb3JlIGZyb20gaGVyZToKaHR0cDovL2Vucmljby5iZXJ0aW5pLmlvL3RlYWNoaW5nLwotLT4KCgojIyBFbnNlbWJsZSBQbG90cyBhbmQgRmFjZXRpbmcKClVzaW5nIG11bHRpcGxlIGNoYW5uZWxzIGFsbG93cyBhIHNpbmdsZSBwbG90IHRvIHNob3cgYSBsb3Qgb2YgaW5mb3JtYXRpb24uCgpCdXQgb3Zlci1wbG90dGluZyBhbmQgaW50ZXJmZXJlbmNlIGNhbiBiZWNvbWUgcHJvYmxlbXMuCgpPbmUgYWx0ZXJuYXRpdmUgaXMgdG8gdXNlIHNldmVyYWwgcmVsYXRlZCB2aWV3cyBpbiBhIHVzZWZ1bCBhcnJhbmdlbWVudC4KClN1Y2ggYXJyYW5nZW1lbnRzIGFyZSBzb21ldGltZXMgY2FsbGVkIF9lbnNlbWJsZSBwbG90c18uCgpUaGVyZSBhcmUgYSBudW1iZXIgb2YgdmFyaWF0aW9uczsgYSBmZXcgYXJlIGludHJvZHVjZWQgYmVsb3cuCgoKIyMjIFNpbWlsYXIgUGxvdHMgd2l0aCBEaWZmZXJlbnQgVmFyaWFibGVzIGFuZCBTaGFyZWQgRW5jb2RpbmdzCgpPbmUgd2F5IHRvIHNob3cgdGhyZWUgY29udGludW91cyB2YXJpYWJsZXMgaXMgd2l0aCB0d28gcGxvdHMgdGhhdApzaGFyZSBhbiBheGlzOgoKYGBge3IsIGZpZy5oZWlnaHQgPSAzLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KbGlicmFyeShwYXRjaHdvcmspCnBlX3RobSA8LSB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUocGFuZWwuYmFja2dyb3VuZCA9IGVsZW1lbnRfcmVjdChjb2xvciA9ICJibGFjayIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGxpbmV3aWR0aCA9IDAuNSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgZmlsbCA9IE5BKSkKCnAxIDwtIGdncGxvdChnbTIwMDcsIGFlcyh4ID0gZ2RwUGVyY2FwLCB5ID0gbGlmZUV4cCwgY29sb3IgPSBjb250aW5lbnQpKSArCiAgICBnZW9tX3BvaW50KCkgKwogICAgc2NhbGVfeF9sb2cxMCgpICsKICAgIGd1aWRlcyhjb2xvciA9ICJub25lIikgKwogICAgcGVfdGhtCnAyIDwtIGdncGxvdChnbTIwMDcsIGFlcyh4ID0gcG9wIC8gMTAgXiA2LCB5ID0gbGlmZUV4cCwgY29sb3IgPSBjb250aW5lbnQpKSArCiAgICBnZW9tX3BvaW50KCkgKwogICAgc2NhbGVfeF9sb2cxMCgpICsKICAgIHBlX3RobSArCiAgICB0aGVtZShheGlzLnRpdGxlLnkgPSBlbGVtZW50X2JsYW5rKCksCiAgICAgICAgICBheGlzLnRleHQueSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGlja3MueSA9IGVsZW1lbnRfYmxhbmsoKSkKcDEgKyBwMgpgYGAKCkxpZmUgZXhwZWN0YW5jeSBpcyBtYXBwZWQgdG8gdGhlIHZlcnRpY2FsIHBvc2l0aW9uIGluIGJvdGggcGxvdHMuCgpDb250aW5lbnQgaXMgbWFwcGVkIHRvIGNvbG9yIGluIGJvdGggcGxvdHMuCgpHdWlkZXMgY2FuIGJlIHNoYXJlZCB3aGVuIGVuY29kaW5ncyBhcmUgc2hhcmVkLgoKCiMjIyBEaWZmZXJlbnQgUGxvdHMgd2l0aCBTaGFyZWQgRW5jb2RpbmdzCgpNdWx0aXBsZSB2aWV3cyBvZiB0aGUgZGF0YSBhcmUgb2Z0ZW4gaGVscGZ1bC4KClNoYXJpbmcgZW5jb2RpbmdzIG1ha2VzIHRoZSByZWxhdGlvbnMgYmV0d2VlbiB2aWV3cyBlYXNpZXIgdG8gcGVyY2VpdmUuCgpgYGB7ciwgZmlnLmhlaWdodCA9IDMsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpwMyA8LSBnZ3Bsb3QoZ20yMDA3LAogICAgICAgICAgICAgYWVzKHggPSBwb3AgLyAxMCBeIDYsCiAgICAgICAgICAgICAgICAgeSA9IHJlb3JkZXIoY29udGluZW50LCBwb3AsIEZVTiA9IHN1bSksCiAgICAgICAgICAgICAgICAgZmlsbCA9IGNvbnRpbmVudCkpICsKICAgIGdlb21fY29sKCkgKwogICAgeWxhYihOVUxMKSArCiAgICBwZV90aG0KcDEgKyBwMwpgYGAKCgojIyMgU21hbGwgTXVsdGlwbGVzCgpfU21hbGwgbXVsdGlwbGVzXyByZWZlcnMgdG8gYSBjb2xsZWN0aW9uIG9mIHBsb3RzIHdpdGggaWRlbnRpY2FsCnN0cnVjdHVyZSBzaG93aW5nIGRpZmZlcmVudCBzdWJzZXRzIG9mIHRoZSBkYXRhIGFuZCBvcmdhbml6ZWQgaW4gYQp1c2VmdWwgd2F5LgoKVGhlc2UgcGxvdCBjb2xsZWN0aW9ucyBhcmUgYWxzbyBjYWxsZWQgX3RyZWxsaXMgcGxvdHNfLCBfbGF0dGljZQpwbG90c18sIG9yIF9mYWNldGVkIHBsb3RzXy4KCkEgcGxvdCBvZiBsaWZlIGV4cGVjdGFuY3kgYWdhaW5zdCBpbmNvbWUgcGVyIGNhcGl0YSBpbiAyMDA3IGZhY2V0ZWQgYnkKY29udGluZW50OgoKYGBge3IsIGZpZy53aWR0aCA9IDgsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZCA8LSBmaWx0ZXIoZ2FwbWluZGVyLCB5ZWFyICVpbiUgYygxOTc3LCAxOTg3LCAxOTk3LCAyMDA3KSkKZ2QyMDA3IDwtIGZpbHRlcihnYXBtaW5kZXIsIHllYXIgPT0gMjAwNykKZmN0X3RobSA8LSB0aGVtZV9taW5pbWFsKCkgKwogICAgdGhlbWUocGFuZWwuYmFja2dyb3VuZCA9IGVsZW1lbnRfcmVjdChjb2xvciA9ICJibGFjayIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIGxpbmV3aWR0aCA9IDAuNSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgZmlsbCA9IE5BKSkKZ2dwbG90KGdkMjAwNywgYWVzKHggPSBnZHBQZXJjYXAsIHkgPSBsaWZlRXhwLCBjb2xvciA9IGNvbnRpbmVudCkpICsKICAgIGdlb21fcG9pbnQoc2l6ZSA9IDIuNSkgKwogICAgc2NhbGVfeF9sb2cxMCgpICsKICAgIGZhY2V0X3dyYXAofiBjb250aW5lbnQpICsKICAgIGZjdF90aG0KYGBgCgpBIHVzZWZ1bCB2YXJpYXRpb24gaXMgdG8gc2hvdyBhIG11dGVkIHZpZXcgb2YgdGhlIGZ1bGwgZGF0YSBpbiB0aGUKYmFja2dyb3VuZDoKCmBgYHtyLCBmaWcud2lkdGggPSA4LCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGdkMjAwNywgYWVzKHggPSBnZHBQZXJjYXAsIHkgPSBsaWZlRXhwLCBjb2xvciA9IGNvbnRpbmVudCkpICsKICAgIGdlb21fcG9pbnQoZGF0YSA9IG11dGF0ZShnZDIwMDcsIGNvbnRpbmVudCA9IE5VTEwpLCBjb2xvciA9ICJncmV5ODAiKSArCiAgICBnZW9tX3BvaW50KHNpemUgPSAyLjUpICsKICAgIHNjYWxlX3hfbG9nMTAoKSArCiAgICBmYWNldF93cmFwKH4gY29udGluZW50KSArCiAgICBmY3RfdGhtCmBgYAoKRGF0YSBjYW4gYmUgZmFjZXRldCBvbiB0d28gdmFyaWFibGVzLgoKVGhpcyBwbG90IHNob3dzIHRoZSBmdWxsIGRhdGEKZmFjZXRlZCBieSBib3RoIGNvbnRpbmVudCBhbmQgYSBzZXQgb2YgeWVhcnM6CgpgYGB7ciwgZmlnLndpZHRoID0gNywgZmlnLmhlaWdodCA9IDcsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZ2QsIGFlcyh4ID0gZ2RwUGVyY2FwLCB5ID0gbGlmZUV4cCwgY29sb3IgPSBjb250aW5lbnQpKSArCiAgICBnZW9tX3BvaW50KHNpemUgPSAyLjUpICsKICAgIHNjYWxlX3hfbG9nMTAoKSArCiAgICBmYWNldF9ncmlkKGNvbnRpbmVudCB+IHllYXIpICsKICAgIGZjdF90aG0KYGBgCgpBZGRpbmcgbXV0ZWQgZGF0YSBmb3IgZWFjaCB5ZWFyIGhlbHBzIHJlZ29uaXppbmcgd2hlcmUgZWFjaApjb250aW5lbnQgZ3JvdXAgZml0cyB3aXRoaW4gYSB5ZWFyCgpgYGB7ciwgZmlnLndpZHRoID0gNywgZmlnLmhlaWdodCA9IDcsIGNsYXNzLnNvdXJjZSA9ICJmb2xkLWhpZGUifQpnZ3Bsb3QoZ2QsIGFlcyh4ID0gZ2RwUGVyY2FwLCB5ID0gbGlmZUV4cCwgY29sb3IgPSBjb250aW5lbnQpKSArCiAgICBnZW9tX3BvaW50KGRhdGEgPSBtdXRhdGUoZ2QsIGNvbnRpbmVudCA9IE5VTEwpLCBjb2xvciA9ICJncmV5ODAiKSArCiAgICBnZW9tX3BvaW50KHNpemUgPSAyLjUpICsKICAgIHNjYWxlX3hfbG9nMTAoKSArCiAgICBmYWNldF9ncmlkKGNvbnRpbmVudCB+IHllYXIpICsKICAgIGZjdF90aG0KYGBgCgpBIFtyZWNlbnQgZXhhbXBsZV0oCmh0dHBzOi8vd3d3LmZ0LmNvbS9jb250ZW50LzI5ZmQ5YjVjLTJmMzUtNDFiZi05ZDRjLTk5NGRiNGUxMjk5OCkgZnJvbQp0aGUgRmluYW5jaWFsIFRpbWVzOgoKYGBge3IgZWNobyA9IEZBTFNFLCBvdXQud2lkdGggPSAiNzAlIn0Ka25pdHI6OmluY2x1ZGVfZ3JhcGhpY3MoSU1HKCJGVC1nZW5kZXItcG9saXRpY3MuanBlZyIpKQpgYGAKCgojIyBSZWFkaW5nCgpTZWN0aW9uIFtfUGVyY2VwdGlvbiBhbmQgRGF0YQpWaXN1YWxpemF0aW9uX10oaHR0cHM6Ly9zb2N2aXouY28vbG9va2F0ZGF0YS5odG1sI3BlcmNlcHRpb24tYW5kLWRhdGEtdmlzdWFsaXphdGlvbikKaW4gW19EYXRhIFZpc3VhbGl6YXRpb25fXShodHRwczovL3NvY3Zpei5jby8pLgoKQ2hhcHRlciBbX0RhdGEgdmlzdWFsaXphdGlvbgpwcmluY2lwbGVzX10oaHR0cHM6Ly9yYWZhbGFiLmRmY2kuaGFydmFyZC5lZHUvZHNib29rLXBhcnQtMS9kYXRhdml6L2RhdGF2aXotcHJpbmNpcGxlcy5odG1sKQppbiBbX0ludHJvZHVjdGlvbiB0byBEYXRhIFNjaWVuY2U6IERhdGEgQW5hbHlzaXMgYW5kIFByZWRpY3Rpb24KQWxnb3JpdGhtcyB3aXRoIFJfXShodHRwczovL3JhZmFsYWIuZGZjaS5oYXJ2YXJkLmVkdS9kc2Jvb2stcGFydC0xLykuCgoKIyMgRXhlcmNpc2VzCgoxLiBXaGljaCBvZiB0aGUgZm9sbG93aW5nIGNoYW5uZWxzIGFyZSBtYWduaXR1ZGUgY2hhbm5lbHMgYW5kIHdoaWNoCiAgIGFyZSBpZGVudGl0eSBjaGFubmVscz8KCiAgICBhLiBQb3NpdGlvbiBvbiBhIGNvbW1vbiBzY2FsZQogICAgYi4gTGVuZ3RoCiAgICBjLiBDb2xvciBodWUgKHJlZCwgZ3JlZW4sIGV0Yy4pCiAgICBkLiBTeW1ib2wgc2hhcGUgKGRvdCwgY3Jvc3MsIGV0Yy4pCgoyLiBDb25zaWRlciB0aGUgZm9sbG93aW5nIHZpc3VhbGl6YXRpb25zIG9mIHRoZSAyMDE3IE1pY2hlbGluIHN0YXIKICAgZGF0YToKCmBgYHtyLCBpbmNsdWRlID0gRkFMU0V9CnBsb3QubmV3KCkKbWljaGVsaW4gPC0gcmVhZC50YWJsZShXTE5LKCJtaWNoZWxpbi5kYXQiKSwKICAgICAgICAgICAgICAgICAgICAgICBoZWFkID0gVFJVRSkKbWljaGVsaW4gPC0gbXV0YXRlKG1pY2hlbGluLAogICAgICAgICAgICAgICAgICAgc3RhcnMgPSBvbmUgKyAyICogdHdvICsgMyAqIHRocmVlLAogICAgICAgICAgICAgICAgICAgIyMgR2V0IHN0cndpZHRoIGZyb20gYmFzZSBncmFwaGljcy4KICAgICAgICAgICAgICAgICAgICMjIE5vdCByaWdodCBidXQgbWF5IGJlIE9LIGZvciB3dWljayB1c2UuCiAgICAgICAgICAgICAgICAgICBzdHJ3aWR0aCA9IDUwMCAqIHN0cndpZHRoKGNvdW50cnksICJpbmNoZXMiKSwKICAgICAgICAgICAgICAgICAgIGNvdW50cnkgPSByZW9yZGVyKGNvdW50cnksIHN0YXJzKSkKYGBgCmBgYHtyLCBlY2hvID0gRkFMU0V9CmxpYnJhcnkoZHBseXIsIHdhcm4uY29uZmxpY3RzID0gRkFMU0UpCmxpYnJhcnkoZ2dwbG90MikKCnAxIDwtIGdncGxvdChtaWNoZWxpbiwgYWVzKHggPSAwLCB5ID0gY291bnRyeSwgbGFiZWwgPSBjb3VudHJ5KSkgKwogICAgZ2VvbV90ZXh0KGhqdXN0ID0gMCwgc2l6ZSA9IDQpICsKICAgIGdlb21fdGlsZShhZXMoeCA9IHN0cndpZHRoICsgc3RhcnMgLyAyLAogICAgICAgICAgICAgICAgICB3aWR0aCA9IHN0YXJzKSwKICAgICAgICAgICAgICBoZWlnaHQgPSAwLjUsCiAgICAgICAgICAgICAgZmlsbCA9ICJkZWVwc2t5Ymx1ZSIpICsKICAgIHhsaW0oYygwLCAxMDAwKSkgKwogICAgdGhlbWVfbWluaW1hbCgpICsKICAgIHRoZW1lKHRleHQgPSBlbGVtZW50X3RleHQoc2l6ZSA9IDE0KSwKICAgICAgICAgIGF4aXMudGV4dC55ID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgYXhpcy50aWNrcy55ID0gZWxlbWVudF9ibGFuaygpKSArCiAgICB5bGFiKE5VTEwpICsKICAgIHhsYWIoTlVMTCkgKwogICAgZ2d0aXRsZSgiUGxvdCBBIikKCnAyIDwtIGdncGxvdChtaWNoZWxpbiwgYWVzKHggPSBzdGFycywgeSA9IGNvdW50cnksIGxhYmVsID0gY291bnRyeSkpICsKICAgIGdlb21fdGlsZShhZXMoeCA9IHN0YXJzIC8gMiwKICAgICAgICAgICAgICAgICAgd2lkdGggPSBzdGFycyksCiAgICAgICAgICAgICAgaGVpZ2h0ID0gMC41LAogICAgICAgICAgICAgIGZpbGwgPSAiZGVlcHNreWJsdWUiKSArCiAgICBnZW9tX3RleHQoaGp1c3QgPSAwLCBzaXplID0gNCwgbnVkZ2VfeCA9IDMwKSArCiAgICB4bGltKGMoMCwgMTAwMCkpICsKICAgIHRoZW1lX21pbmltYWwoKSArCiAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxNCksCiAgICAgICAgICBheGlzLnRleHQueSA9IGVsZW1lbnRfYmxhbmsoKSwKICAgICAgICAgIGF4aXMudGlja3MueSA9IGVsZW1lbnRfYmxhbmsoKSkgKwogICAgeWxhYihOVUxMKSArCiAgICB4bGFiKE5VTEwpICsKICAgIGdndGl0bGUoIlBsb3QgQiIpCgpwMSArIHAyCmBgYAoKV2hpY2ggcGxvdCBtYWtlcyBpdCBlYXNpZXIgdG8gY29tcGFyZSB0aGUgbnVtYmVycyBvZiBzdGFycyBmb3IKZGlmZmVyZW50IGNvdW50cmllcz8gRXhwbGFpbiB5b3VyIGNvbmNsdXNpb24gYnkgaWRlbnRpZnlpbmcgdGhlCmNoYW5uZWxzIHVzZWQgYW5kIHRoZWlyIHJlbGF0aXZlIHN0cmVuZ3Rocy4KCjMuIElkZW50aWZ5IHRoZSBpdGVtcywgYXR0cmlidXRlcywgbWFya3MsIGNoYW5uZWxzLCBhbmQgbWFwcGluZ3MgdXNlCiAgIGluIHRoZSBmb2xsb3dpbmcgcGxvdDoKCmBgYHtyLCBlY2hvID0gRkFMU0V9CmxpYnJhcnkoZHBseXIsIHdhcm4uY29uZmxpY3RzID0gRkFMU0UpCmxpYnJhcnkoZ2dwbG90MikKCm11dGF0ZShtcGcsIGN5bCA9IGZhY3RvcihjeWwpKSB8PgogICAgZ3JvdXBfYnkoY3lsLCB5ZWFyKSB8PgogICAgc3VtbWFyaXplKGh3eSA9IG1lYW4oaHd5KSwgY3R5ID0gbWVhbihjdHkpLCBDb3VudCA9IG4oKSkgfD4KICAgIHVuZ3JvdXAoKSB8PgogICAgbXV0YXRlKGN5bCA9IGZhY3RvcihjeWwpLCB5ZWFyID0gZmFjdG9yKHllYXIpKSB8PgogICAgZ2dwbG90KGFlcyh4ID0geWVhciwgeSA9IGh3eSwgc2l6ZSA9IENvdW50LCBjb2xvciA9IGN5bCkpICsKICAgIGdlb21fcG9pbnQoKSArCiAgICBzY2FsZV9zaXplX2FyZWEobWF4X3NpemUgPSAxNSkgKwogICAgdGhlbWVfbWluaW1hbCgpICsgc2NhbGVfY29sb3JfdmlyaWRpc19kKCkKYGBgCg==
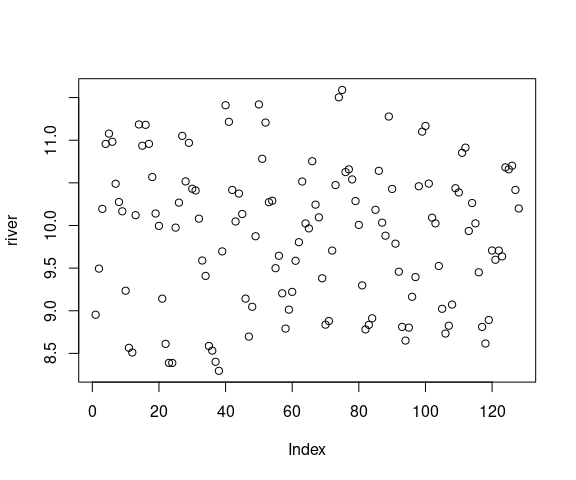
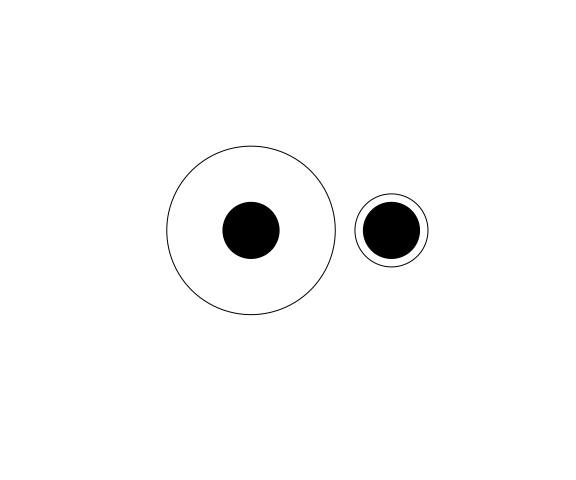


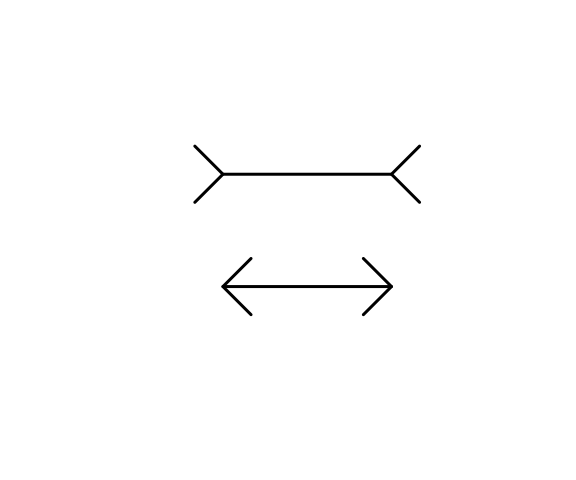

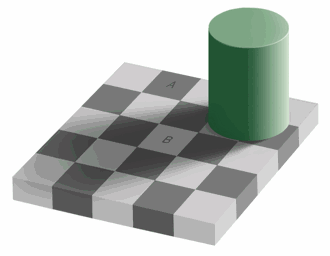





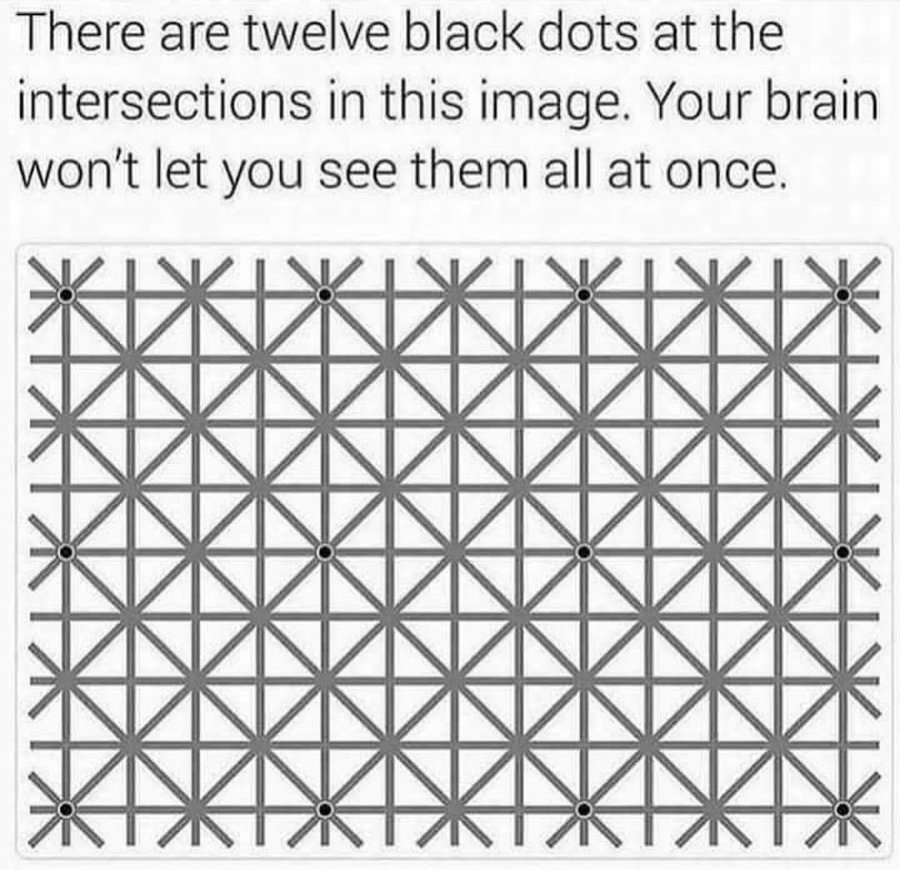








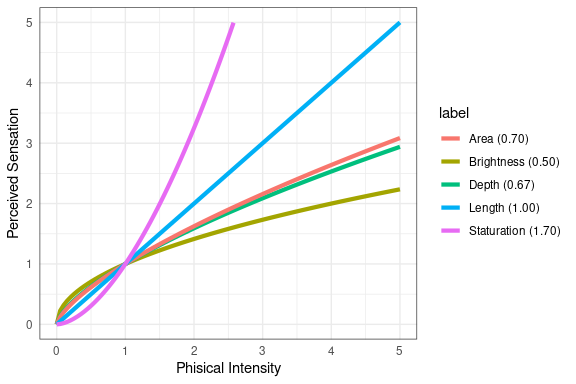
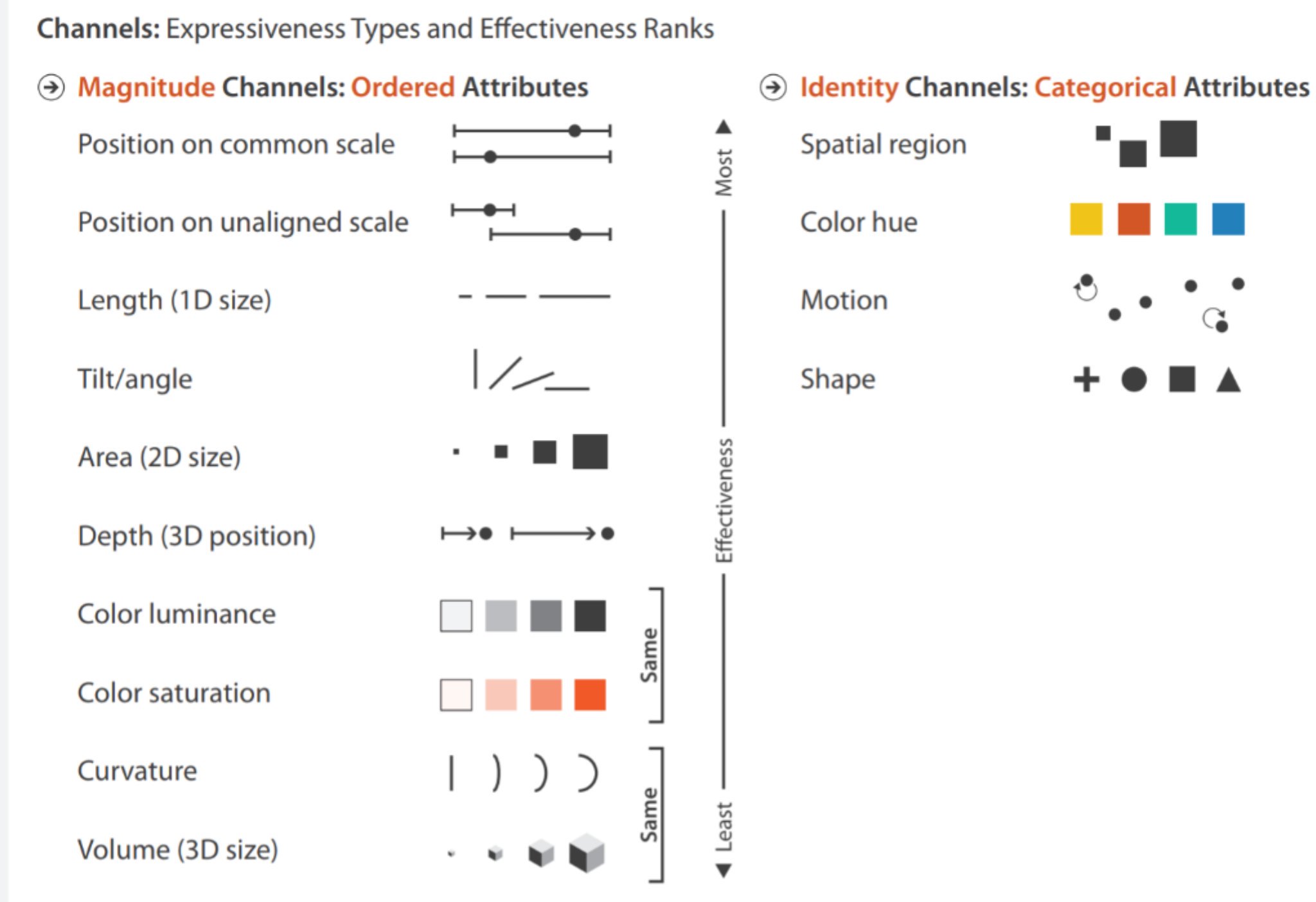 This ordering is sometimes referred to as a perceptual ladder.
This ordering is sometimes referred to as a perceptual ladder.