University of Iowa

College of Liberal Arts and Sciences

• STAT:4580
• Syllabus
• Outline
• Homework
• Notes
• Resources
-->

ECDF, QQ, and PP Plots

Cumulative Distribution and Survival Functions

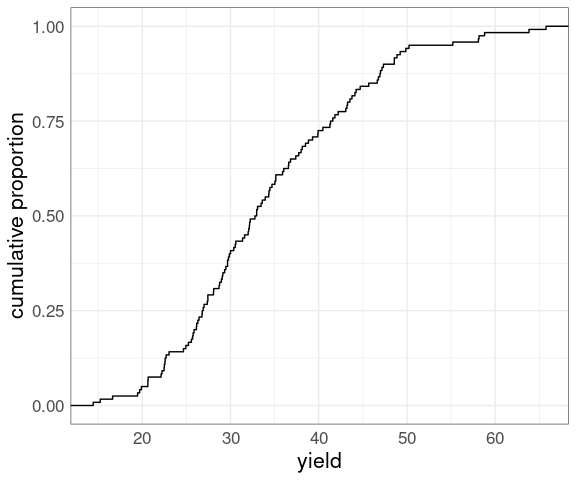
The empirical cumulative distribution function (ECDF) of a numeric sample computes the proportion of the sample at or below a specified value.

For the yields of the barley data:

library(ggplot2)
data(barley, package = "lattice")
thm <- theme_minimal() +
    theme(text = element_text(size = 16)) +
    theme(panel.border =
          element_rect(color = "grey30",
                       fill = NA))
p <- ggplot(barley) +
    stat_ecdf(aes(x = yield)) +
    ylab("cumulative proportion") +
    thm
p

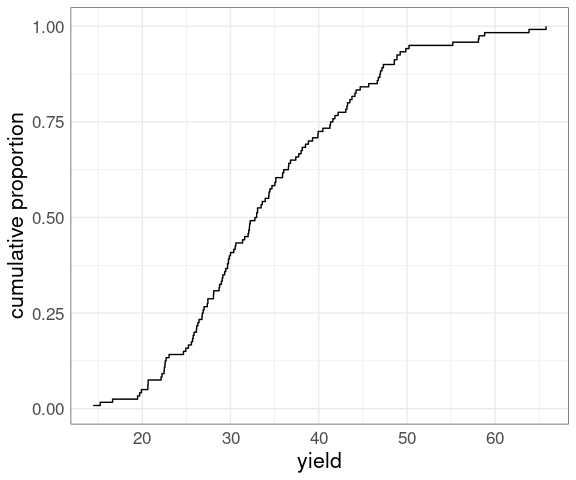
Flipping the axes produces an empirical quantile plot:

p + coord_flip()

Both make it easy to look up:

• medians, quartiles, and other quantiles;

• the proportion of the sample below a particular value;

• the proportion above a particular value (one minus the proportion below).

An ECDF plot can also be constructed as a step function plot of the relative rank (rank over sample size) against the observed values:

ggplot(barley) +
    geom_step(
        aes(x = yield,
            y = rank(yield) /
                length(yield))) +
    ylab("cumulative proportion") +
    thm

Reversing the relative ranks produces a plot of the empirical survival function:

ggplot(barley) +
    geom_step(
        aes(x = yield,
            y = rank(-yield) /
                length(yield))) +
    ylab("surviving proportion") +
    thm

Survival plots are often used for data representing time to failure in engineering or time to death or disease recurrence in medicine.

For a highly skewed distribution, such as the distribution of price in the diamonds data, transforming the axis to a square root or log scale may help.

library(patchwork)
p1 <- ggplot(diamonds) +
    stat_ecdf(aes(x = price)) +
    ylab("cumulative proportion") +
    thm
p2 <- p1 + scale_x_log10()
p1 + p2

There is a downside: Interpolating on a non-linear scale is much harder.

QQ Plots

Basics

One way to assess how well a particular theoretical model describes a data distribution is to plot data quantiles against theoretical quantiles.

This corresponds to transforming the ECDF horizontal axis to the scale of the theoretical distribution.

The result is a plot of sample quantiles against theoretical quantiles, and should be close to a 45-degree straight line if the model fits the data well.

Such a plot is called a quantile-quantile plot, or a QQ plot for short.

Usually a QQ plot

• uses points rather than a step function, and

• 1/2 is subtracted from the ranks before calculating relative ranks (this makes the rank range more symmetric):

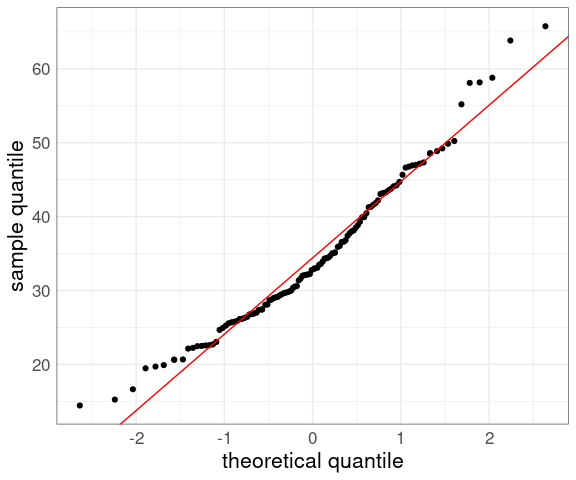
For the barley data:

p <- ggplot(barley) +
    geom_point(
        aes(y = yield,
            x = qnorm((rank(yield) - 0.5) /
                      length(yield)))) +
    xlab("theoretical quantile") +
    ylab("sample quantile") +
    thm
p

For a location-scale family of models, like the normal family, a QQ plot against standard normal quantiles should be close to a straight line if the model is a good fit.

For the normal family the intercept will be the mean and the slope will be the standard deviation.

Adding a line can help judge the quality of the fit:

p + geom_abline(aes(intercept = mean(yield),
                    slope = sd(yield)),
                color = "red")

ggplot provides geom_qq that makes this a little easier; base graphics provides qqnorm and lattice has qqmath.

Some Examples

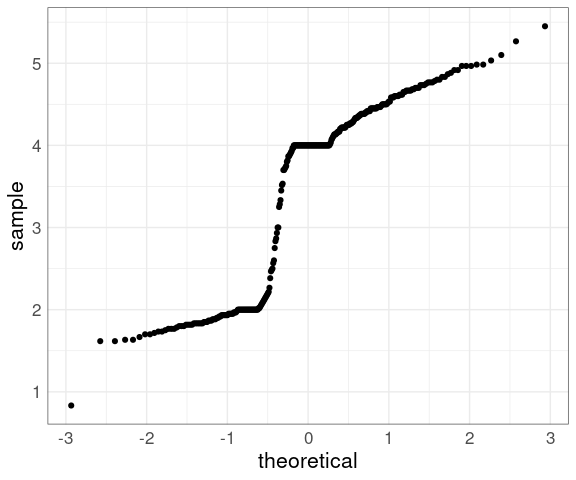
The histograms and density estimates for the duration variable in the geyser data set showed that the distribution is far from a normal distribution, and the normal QQ plot shows this as well:

data(geyser, package = "MASS")
ggplot(geyser) +
    geom_qq(aes(sample = duration)) +
    thm

Except for rounding the parent heights in the Galton data seemed not too far from normally distributed:

data(Galton, package = "HistData")
ggplot(Galton) +
    geom_qq(aes(sample = parent)) +
    thm

• Rounding interferes more with this visualization than with a histogram or a density plot.

• Rounding is more visible with this visualization than with a histogram or a density plot.

Another Gatlton dataset available in the UsingR package with less rounding is father.son:

data(father.son, package = "UsingR")
ggplot(father.son) +
    geom_qq(aes(sample = fheight)) +
    thm

The middle seems to be fairly straight, but the ends are somewhat wiggly.

How can you calibrate your judgment?

Calibrating the Variability

One approach is to use simulation, sometimes called a graphical bootstrap.

The nboot function will simulate R samples from a normal distribution that match a variable x on sample size, sample mean, and sample SD.

The result is returned in a data frame suitable for plotting:

library(dplyr)
nsim <- function(n, m = 0, s = 1) {
    z <- rnorm(n)
    m + s * ((z - mean(z)) / sd(z))
}

nboot <- function(x, R) {
    n <- length(x)
    m <- mean(x)
    s <- sd(x)
    sim <- function(i) {
        xx <- sort(nsim(n, m, s))
        p <- (seq_along(x) - 0.5) / n
        data.frame(x = xx, p = p, sim = i)
    }
    bind_rows(lapply(1 : R, sim))
}

Plotting these as lines shows the variability in shapes we can expect when sampling from the theoretical normal distribution:

gb <- nboot(father.son$fheight, 50)
ggplot() +
    geom_line(aes(x = qnorm(p),
                  y = x,
                  group = sim),
              color = "gray", data = gb) +
    thm

We can then insert this simulation behind our data to help calibrate the visualization:

ggplot(father.son) +
    geom_line(aes(x = qnorm(p),
                  y = x,
                  group = sim),
              color = "gray", data = gb) +
    geom_qq(aes(sample = fheight)) +
    thm

Scalability

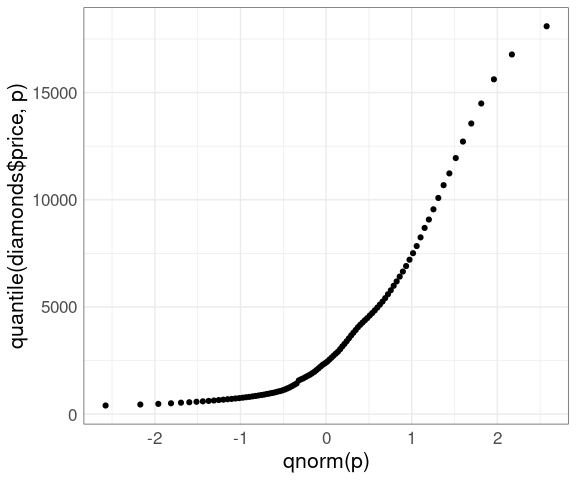
For large sample sizes, such as price from the diamonds data, overplotting will occur:

ggplot(diamonds) +
    geom_qq(aes(sample = price)) +
    thm

This can be alleviated by using a grid of quantiles:

nq <- 100
p <- ((1 : nq) - 0.5) / nq
ggplot() +
    geom_point(aes(x = qnorm(p),
                   y = quantile(diamonds$price, p))) +
    thm

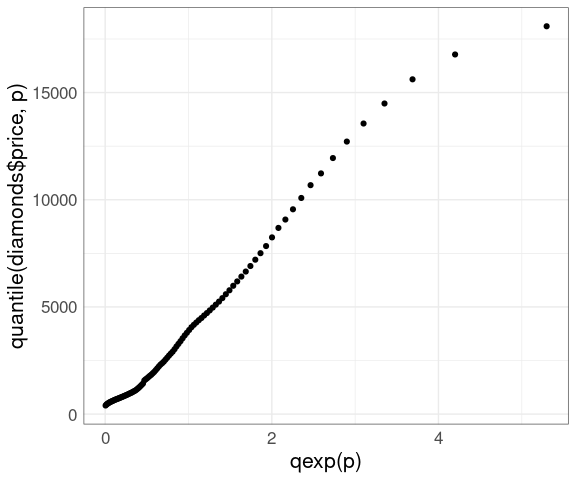
A more reasonable model might be an exponential distribution:

ggplot() +
    geom_point(aes(x = qexp(p), y = quantile(diamonds$price, p))) +
    thm

Comparing Two Distributions

The QQ plot can also be used to compare two distributions based on a sample from each.

If the samples are the same size then this is just a plot of the ordered sample values against each other.

Choosing a fixed set of quantiles allows samples of unequal size to be compared.

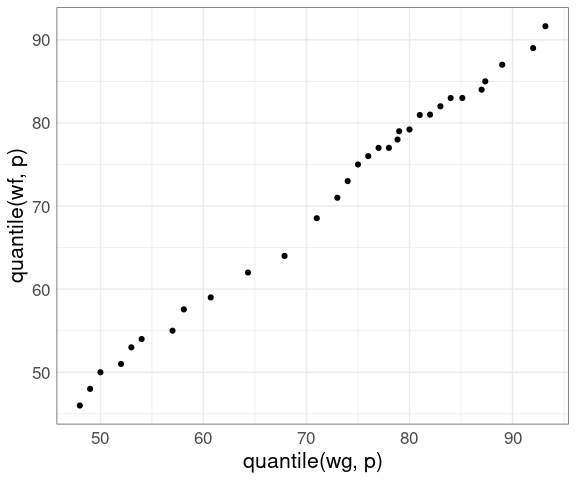
Using a small set of quantiles we can compare the distributions of waiting times between eruptions of Old Faithful from the two different data sets we have looked at:

nq <- 31
p <- (1 : nq) / nq - 0.5 / nq
wg <- geyser$waiting
wf <- faithful$waiting
ggplot() +
    geom_point(aes(x = quantile(wg, p),
                   y = quantile(wf, p))) +
    thm

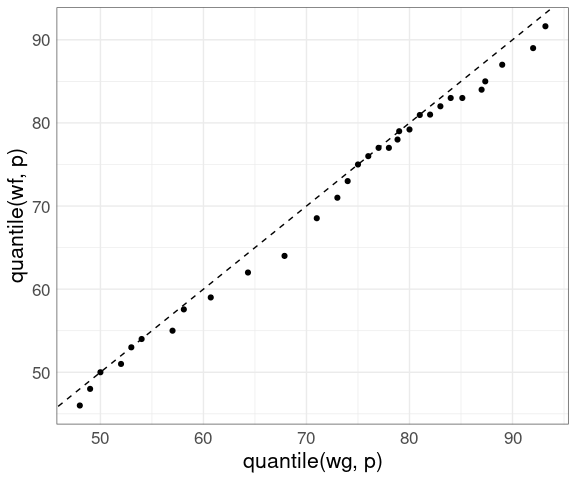
Adding a 45-degree line:

ggplot() +
    geom_abline(intercept = 0, slope = 1, lty = 2) +
    geom_point(aes(x = quantile(wg, p), y = quantile(wf, p))) +
    thm

PP Plots

The PP plot for comparing a sample to a theoretical model plots the theoretical proportion less than or equal to each observed value against the actual proportion.

For a theoretical cumulative distribution function \(F\) this means plotting

\[ F(x_i) \sim p_i \]

with

\[ p_i = \frac{r_i - 1/2}{n} \]

where \(r_i\) is the \(i\)-th observation’s rank.

For the fheight variable in the father.son data:

m <- mean(father.son$fheight)
s <- sd(father.son$fheight)
n <- nrow(father.son)
p <- (1 : n) / n - 0.5 / n
ggplot(father.son) +
    geom_point(aes(x = p,
                   y = sort(pnorm(fheight, m, s)))) +
    thm

• The values on the vertical axis are the probability integral transform of the data for the theoretical distribution.

• If the data are a sample from the theoretical distribution then these transforms would be uniformly distributed on \([0, 1]\).

• The PP plot is a QQ plot of these transformed values against a uniform distribution.

• The PP plot goes through the points \((0, 0)\) and \((1, 1)\) and so is much less variable in the tails.

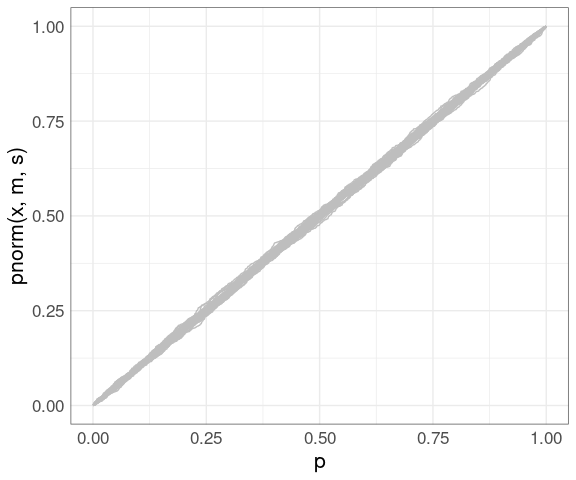
Using the simulated data:

pp <- ggplot() +
    geom_line(aes(x = p,
                  y = pnorm(x, m, s),
                  group = sim),
              color = "gray",
              data = gb) +
    thm
pp

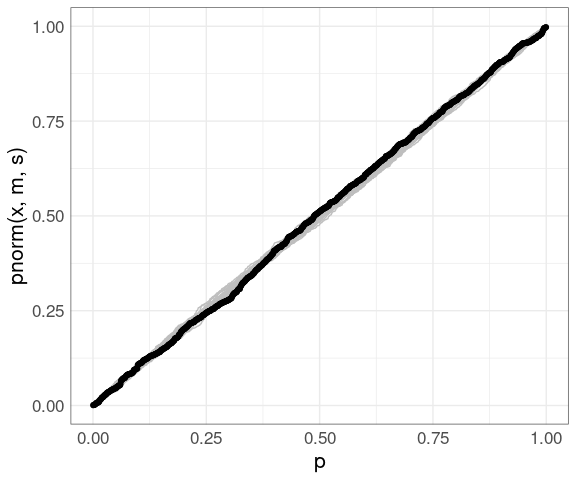
Adding the father.son data:

pp +
    geom_point(aes(x = p, y = sort(pnorm(fheight, m, s))), data = (father.son))

The PP plot is also less sensitive to deviations in the tails.

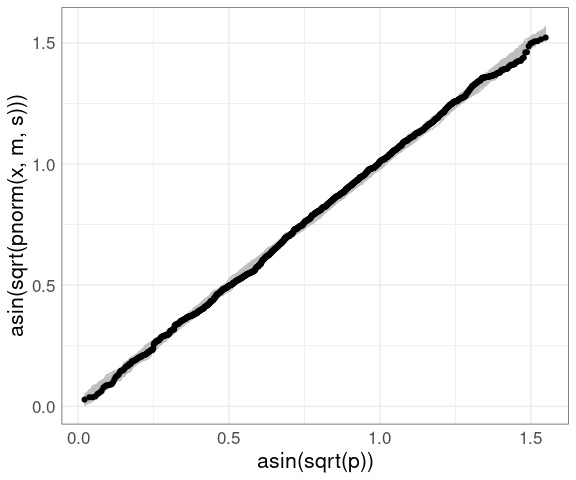
A compromise between the QQ and PP plots uses the arcsine square root variance-stabilizing transformation, which makes the variability approximately constant across the range of the plot:

vpp <- ggplot() +
    geom_line(aes(x = asin(sqrt(p)),
                  y = asin(sqrt(pnorm(x, m, s))),
                  group = sim),
              color = "gray", data = gb) +
    thm
vpp

Adding the data:

vpp +
    geom_point(
        aes(x = asin(sqrt(p)),
            y = sort(asin(sqrt(pnorm(fheight, m, s))))),
        data = (father.son))

Plots For Assessing Model Fit

Both QQ and PP plots can be used to asses how well a theoretical family of models fits your data, or your residuals.

To use a PP plot you have to estimate the parameters first.

For a location-scale family, like the normal distribution family, you can use a QQ plot with a standard member of the family.

Some other families can use other transformations that lead to straight lines for family members.

The Weibull family is widely used in reliability modeling; its CDF is

\[ F(t) = 1 - \exp\left\(-\left(\frac{t}{b}\right)^a\right\)\]

The logarithms of Weibull random variables form a location-scale family.

Special paper used to be available for Weibull probability plots.

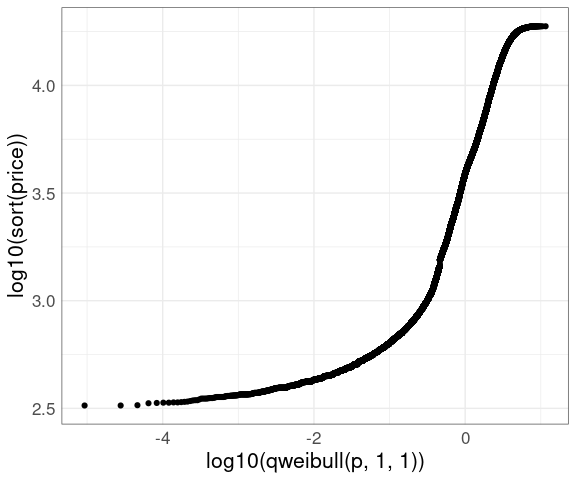
A Weibull QQ plot for price in the diamonds data:

n <- nrow(diamonds)
p <- (1 : n) / n - 0.5 / n
ggplot(diamonds) +
    geom_point(aes(x = log10(qweibull(p, 1, 1)), y = log10(sort(price)))) +
    thm

The lower tail does not match a Weibull distribution.

Is this important?

In engineering applications it often is.

In selecting a reasonable model to capture the shape of this distribution it may not be.

QQ plots are helpful for understanding departures from a theoretical model.

No data will fit a theoretical model perfectly.

Case-specific judgment is needed to decide whether departures are important.

George Box: All models are wrong but some are useful.

Some References

Adam Loy, Lendie Follett, and Heike Hofmann (2016), “Variations of Q–Q plots: The power of our eyes!”, The American Statistician; (preprint).

John R. Michael (1983), “The stabilized probability plot,” Biometrika JSTOR.

M. B. Wilk and R. Gnanadesikan (1968), “Probability plotting methods for the analysis of data,” Biometrika JSTOR.

Box, G. E. P. (1979), “Robustness in the strategy of scientific model building”, in Launer, R. L.; Wilkinson, G. N., Robustness in Statistics, Academic Press, pp. 201–236.

Thomas Lumley (2019), “What have I got against the Shapiro-Wilk test?”

Readings

Chapter Visualizing distributions: Empirical cumulative distribution functions and q-q plots in Fundamentals of Data Visualization.

Exercises

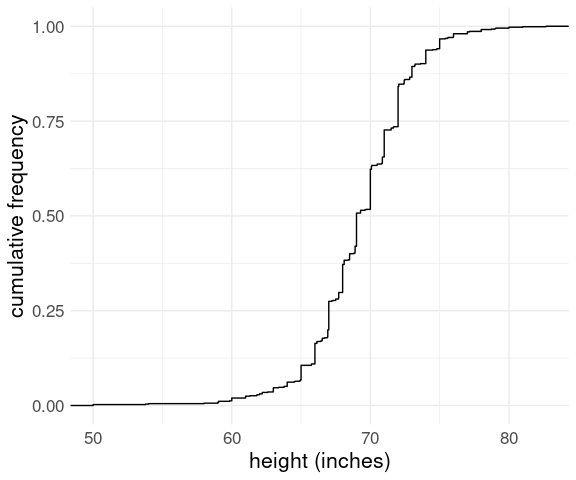
1. The data set heights in package dslabs contains self-reported heights for a number of female and male students. The plot below shows the empirical CDF for male heights:

   

   Based on the plot, what percentage of males are taller than 75 inches?

   1. 100%
   2. 15%
   3. 20%
   4. 3%

2. Consider the following normal QQ plots.

   library(dplyr)
   library(ggplot2)
   library(patchwork)
   thm <- theme_minimal() + theme(text = element_text(size = 16))
   data(heights, package = "dslabs")
   set.seed(12345)
   p1 <- ggplot(NULL, aes(sample = rnorm(200))) +
       geom_qq() +
       labs(title = "Sample 1",
            x = "theoretical quantile",
            y = "sample quantile") +
       thm
   p2 <- ggplot(faithful, aes(sample = eruptions)) +
       geom_qq() +
       labs(title = "Sample 2",
            x = "theoretical quantile",
            y = "sample quantile") +
       thm
   p1 + p2

   

   Would a normal distribution be a reasonable model for either of these samples?

   1. No for Sample 1. Yes for Sample 2.
   2. Yes for Sample 1. No for Sample 2.
   3. Yes for both.
   4. No for both.

This work is licensed under the CC BY-NC 3.0 Creative Commons License.