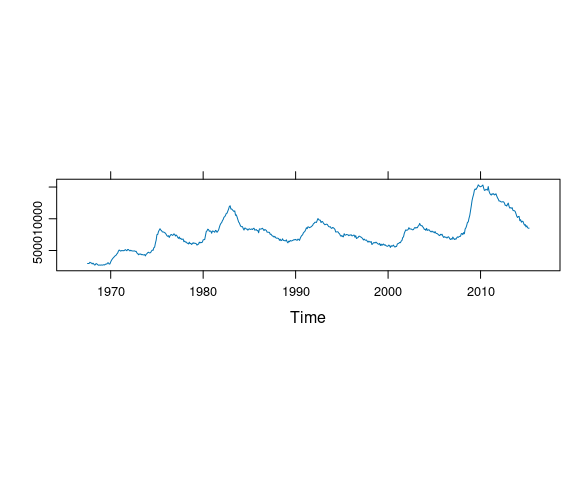
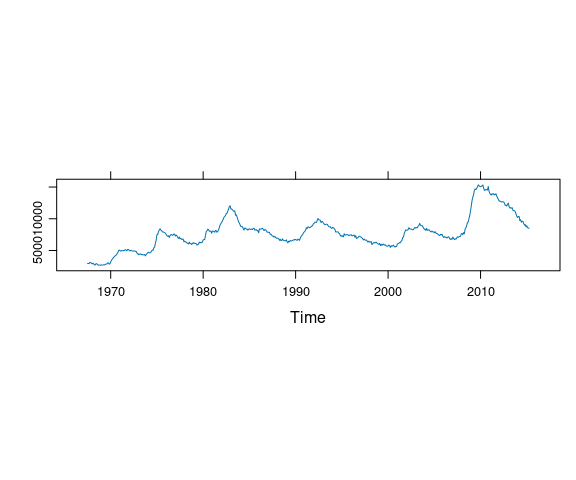
Time Series Data
A lot of data is collected over time:
The objectives can be
understanding the past – how we got where we are;
understanding patterns in variation;
forecasting what will happen next.
Even if time is not of primary interest, data are often collected with a time stamp.
Examining the behavior over time can reveal interesting features that may hint at confounding variables:
Time series data can be collected at regularly spaced intervals:
yearly, e.g. the gapminder data
monthly, e.g. the river data
daily, e.g. high temperatures.
Data might be missing
irregularly, e.g. faulty instrument, holidays;
regularly, e.g. weekends.
Time series can also be recorded at irregular times:
blood pressure at doctor visits;
Variables recorded over time can be numerical or categorical.
Time Series Objects
Time series data can be represented as regular data frames with a time variable.
There are also a number of specialized object classes for dealing with time series.
A number of packages provide plot or autoplot methods and other utilities for these objects.
Some of the most useful:
ts, mtsbaseregular series; methods for plot and lines.
forecastmethods for autoplot and autolayer.
zoozooirregular and regular series; autoplot support.
broomtidy for converting to tidy data frames.
autoplot and autolayerMany data structures provide methods for autoplot and autolayer.
From the autoplot help page:
autoplot uses ggplot2 to draw a particular plot for an object of a particular class in a single command. This defines the S3 generic that other classes and packages can extend.
From the autolayer help page:
autolayer uses ggplot2 to draw a particular layer for an object of a particular class in a single command. This defines the S3 generic that other classes and packages can extend.
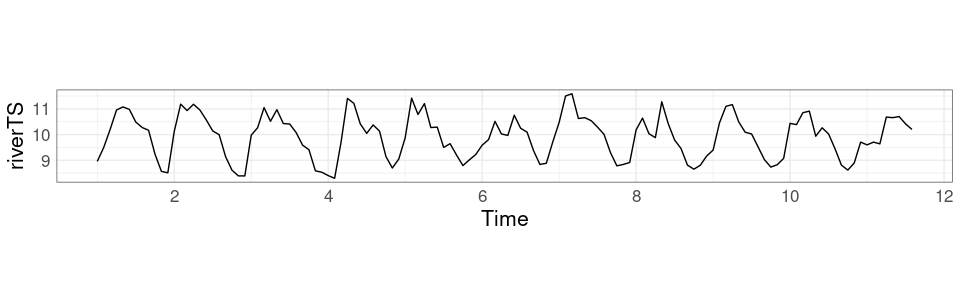
Example: River Data
Creating a ts object for the river data:
river <- scan("https://www.stat.uiowa.edu/~luke/data/river.dat")
(riverTS <- ts(river))
## Time Series:
## Start = 1
## End = 128
## Frequency = 1
## [1] 8.95361 9.49409 10.19430 10.95660 11.07770 10.98170 10.48970 10.27540
## [9] 10.16620 9.23484 8.56537 8.51064
## [ reached getOption("max.print") -- omitted 116 entries ]Or, since the data were collected monthly:
(riverTS <- ts(river, frequency = 12))
## Jan Feb Mar Apr May Jun Jul Aug
## 1 8.95361 9.49409 10.19430 10.95660 11.07770 10.98170 10.48970 10.27540
## Sep Oct Nov Dec
## 1 10.16620 9.23484 8.56537 8.51064
## [ reached getOption("max.print") -- omitted 10 rows ]Using tidy from package broom to create a data frame from the ts object:
riverDF <- broom::tidy(riverTS)
head(riverDF, 3)
## # A tibble: 3 × 2
## index value
## <dbl> <dbl>
## 1 1 8.95
## 2 1.08 9.49
## 3 1.17 10.2Change to more convenient names:
riverDF <- rename(riverDF, time = index, flow = value)
head(riverDF, 3)
## # A tibble: 3 × 2
## time flow
## <dbl> <dbl>
## 1 1 8.95
## 2 1.08 9.49
## 3 1.17 10.2
Basic Plots for a Single Numeric Time Series
Numeric time series are usually plotted as a line chart .
This is what the autoplot method for ts objects provided by package forecast does.
For the river flow data:
library(forecast)
p <- autoplot(riverTS)
pUsing symbols in addition to lines is sometimes useful:
p + geom_point()
Aspect Ratio
Aspect ratio has a significant effect on how well we perceive slope differences.
Controlling the aspect ratio:
For base graphics use the asp argument to plot.
lattice uses the aspect argument.
For ggplot use the ratio argument to coord_fixed.
p + coord_fixed(ratio = 1 / 3)
Lattice supports several aspect ratio strategies:
"fill" to avoid unused white space;
"xy" to use a 45 degree banking rule;
"iso" for isometric scales, e.g. distances.
Some work may be needed to avoid excess white space around figures.
Using multiple panels can help.
In an interactive setting, zoom and pan support can help.
Multiple panels:
mutate(riverDF,
period = cut(time, breaks = 3)) |>
ggplot(aes(time, flow)) +
geom_line() +
facet_wrap(~ period,
scales = "free_x",
ncol = 1)Adding zoom and pan support using plotly
library(plotly)
pp <- p + geom_line() + coord_fixed(ratio = 1 / 3)
ggplotly(pp)
There is not always a single best aspect ratio.
The co2 data set in the datasets package contains monthly concentrations of CO2 for the years 1959 to 1997 recorded at the Mauna Loa observatory.
The co2 data is stored as an object of class ts:
str(co2)
## Time-Series [1:468] from 1959 to 1998: 315 316 316 318 318 ...plot and xyplot have methods for ts objects that simplify time series plotting.
Two aspect ratios:
xyplot(co2)
xyplot(co2, aspect = "xy")
A graph with more recent data is available .
The full data is available as well.
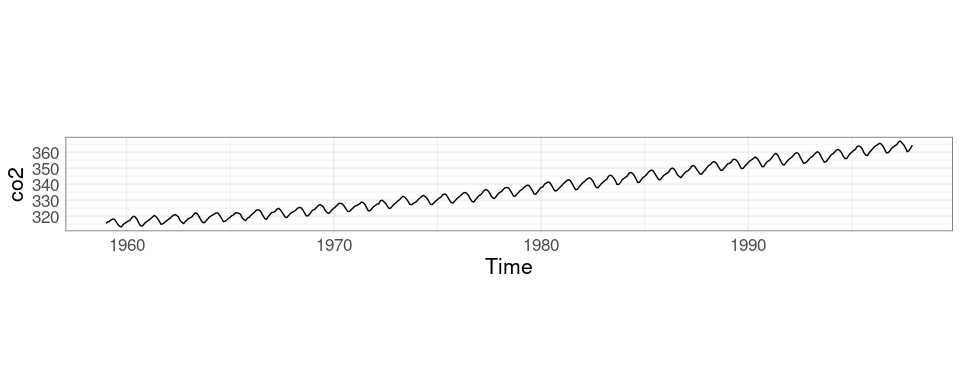
autoplot does not yet provide an easy way to bank to 45 degrees; you need to experiment or calculate an appropriate aspect ratio yourself.
The default autoplot:
library(forecast)
autoplot(co2)Aspect ratio adjusted with coord_fixed:
r45 <- median(diff(time(co2))) / median(abs(diff(co2)))
autoplot(co2) + coord_fixed(ratio = r45)
Updated Mauna Loa CO2 Data
Downloading and reading in the data:
library(lubridate)
url <- "https://gml.noaa.gov/webdata/ccgg/trends/co2/co2_mm_mlo.txt"
if (! file.exists("co2new.dat") ||
now() > file.mtime("co2new.dat") + weeks(4))
download.file(url, "co2new.dat")
co2new <- read.table("co2new.dat")Clean up the variable names:
head(co2new)
## V1 V2 V3 V4 V5 V6 V7 V8
## 1 1958 3 1958.203 315.71 314.44 -1 -9.99 -0.99
## 2 1958 4 1958.288 317.45 315.16 -1 -9.99 -0.99
## 3 1958 5 1958.370 317.51 314.69 -1 -9.99 -0.99
## 4 1958 6 1958.455 317.27 315.15 -1 -9.99 -0.99
## 5 1958 7 1958.537 315.87 315.20 -1 -9.99 -0.99
## 6 1958 8 1958.622 314.93 316.21 -1 -9.99 -0.99
names(co2new) <- c("year", "month", "decimal_date", "average",
"deseason", "ndays", "stdd", "umm")An initial look:
ggplot(co2new, aes(decimal_date, average)) + geom_line()
Missing values are encoded as -9.99 or -99.99.
If there are any such values they need to be replaced with R’s missing value representation:
filter(co2new, average < -9)
## [1] year month decimal_date average deseason
## [6] ndays stdd umm
## <0 rows> (or 0-length row.names)
co2new <- mutate(co2new, average = ifelse(average < -9, NA, average))This produces a reasonable plot:
ggplot(co2new, aes(decimal_date, average)) +
geom_line()
The plot would show gaps for the missing values.
Missing values could also be interpolated with na.interp from package forecast.
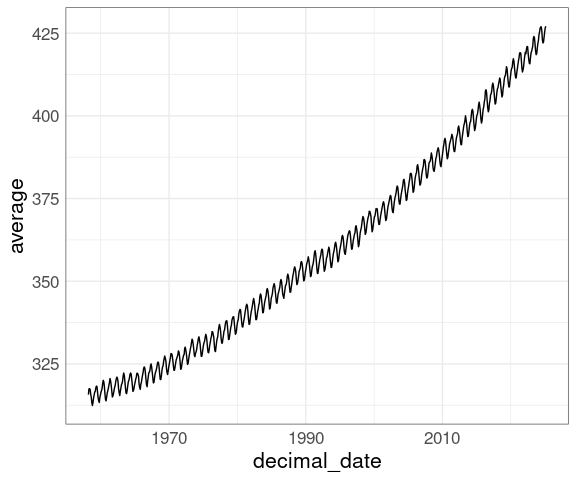
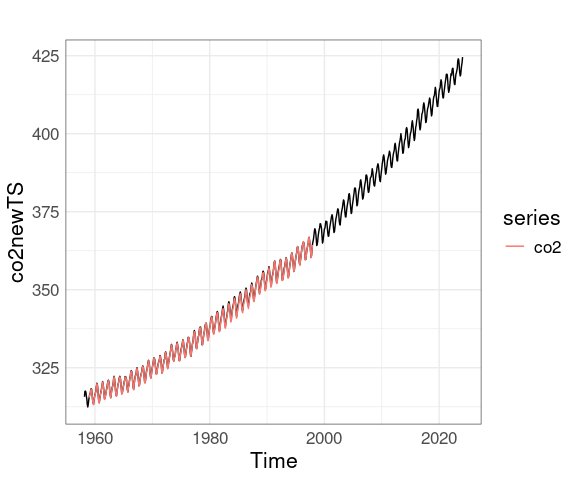
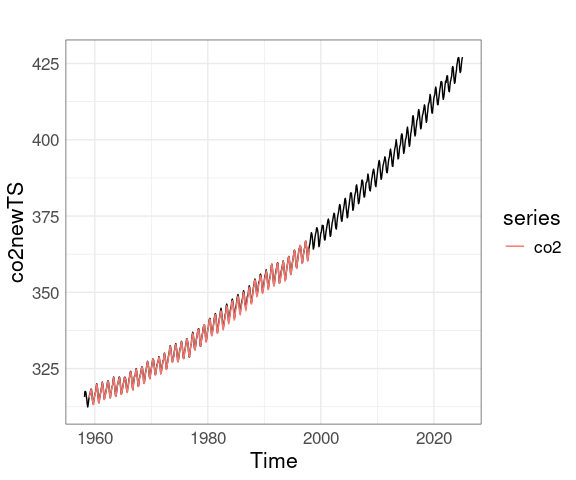
Converting the new data to a ts object makes adding the original data a little easier:
co2newTS <- ts(co2new$average, start = c(1958, 3), frequency = 12)
autoplot(co2newTS) + autolayer(co2)
Seasonal Decomposition of Time Series by Loess (STL)
For time series with a strong seasonal component it can be useful to look at a Seasonal Decomposition of Time Series by Loess , or (STL ).
The methodology was suggested by Clevaland and coworkers.
The stl function in the base package computes such a decomposition.
It requires a series without missing values.
co2newTS_no_NA <- ts(co2new$average, start = c(1958, 3), frequency = 12)
co2stl <- stl(co2newTS_no_NA, s.window = 21)
head(co2stl$time.series)
## seasonal trend remainder
## Mar 1958 1.1159035 314.9426 -0.3484682
## Apr 1958 2.2797196 315.0143 0.1559367
## May 1958 2.7672696 315.0861 -0.3433923
## Jun 1958 2.2272621 315.1579 -0.1151637
## Jul 1958 0.8611739 315.2241 -0.2153025
## Aug 1958 -1.0848309 315.2904 0.7244755Package forecast provides an autoplot method for stl objects that shows the original data and the three components in separate panels:
autoplot(co2stl)
Some Alternative Visualizations
Bar charts are sometimes used when comparison to a base line is important; for example for illustrating climate change .
Calendar plots, or calendar heatmaps, are sometimes useful for displaying daily data where day of the week/weekend effects might be important. One example is available here .
A blog post shows how to build a calendar plot with ggplot.
GDP Growth Data
Bar charts are sometimes used for economic time series, in particular growth rate data.
Some GDP growth rate data is available on this web page :
Read the data from the web page:
library(rvest)
gdpurl <- "http://www.multpl.com/us-real-gdp-growth-rate/table/by-quarter"
gdppage <- read_html(gdpurl)
gdptbl <- html_table(gdppage)[[1]]
head(gdptbl)
## # A tibble: 6 × 2
## Date Value
## <chr> <chr>
## 1 Dec 31, 2024 2.53%
## 2 Sep 30, 2024 2.72%
## 3 Jun 30, 2024 3.04%
## 4 Mar 31, 2024 2.90%
## 5 Dec 31, 2023 3.20%
## 6 Sep 30, 2023 3.24%Clean the data:
library(dplyr)
library(lubridate)
names(gdptbl) <- c("Date", "Value")
gdptbl <- mutate(gdptbl,
Value = as.numeric(sub("%", "", Value)),
Date = mdy(Date))
head(gdptbl)
## # A tibble: 6 × 2
## Date Value
## <date> <dbl>
## 1 2024-12-31 2.53
## 2 2024-09-30 2.72
## 3 2024-06-30 3.04
## 4 2024-03-31 2.9
## 5 2023-12-31 3.2
## 6 2023-09-30 3.24Data prior to 1947 is annual, so drop earlier data:
gdptbl <- filter(gdptbl,
Date >= make_date(1948, 1, 1))Rearrange to put Date in increasing order:
gdptbl <- arrange(gdptbl, Date)Create and plot a time series:
library(ggplot2)
library(forecast)
gdpts <- ts(gdptbl$Value,
start = 1948, frequency = 4)
autoplot(gdpts) +
geom_hline(yintercept = 0, linetype = 2)
A bar chart with color used to distinguish positive and negative growth can be created from the original table gdptbl:
library(ggplot2)
mutate(gdptbl,
growth = ifelse(Value >= 0,
"pos",
"neg")) |>
ggplot(aes(x = Date,
y = Value,
fill = growth)) +
geom_col() +
theme(legend.position = "top") +
scale_fill_manual(
values = c(pos = "blue", neg = "red"))
The bar chart can also be created from the time series object:
data.frame(rate = as.numeric(gdpts),
time = as.numeric(time(gdpts))) |>
mutate(growth = ifelse(rate >= 0,
"pos",
"neg")) |>
ggplot(aes(time, rate, fill = growth)) +
geom_col() +
theme(legend.position = "top") +
scale_fill_manual(
values = c(pos = "blue", neg = "red"))
Airline Flights From NYC
The nycflights13 data set contains data on all flight leaving New York City in 2013.
Similar data is available for other cities and years, e.g. from the anyflights package
We can look at the number of departures for each day:
library(nycflights13)
library(ggplot2)
nf <- count(flights, year, month, day)It will be useful to have a combined date field in our data frame.
The lubridate function make_date can be used for this:
library(lubridate)
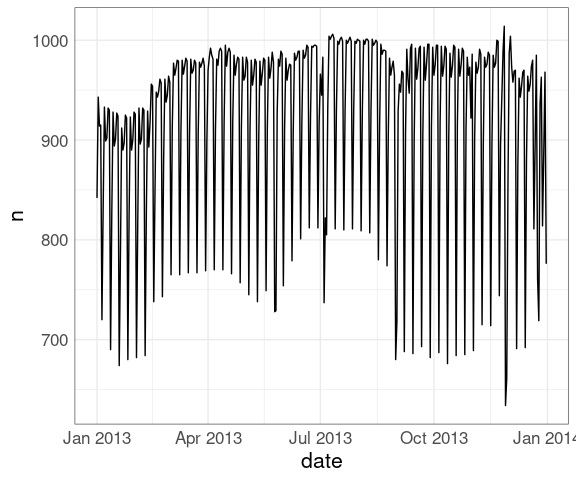
nf <- mutate(nf, date = make_date(year, month, day))A line plot of the number of flights:
ggplot(nf, aes(date, n)) +
geom_line()Weekday variation is clearly visible.
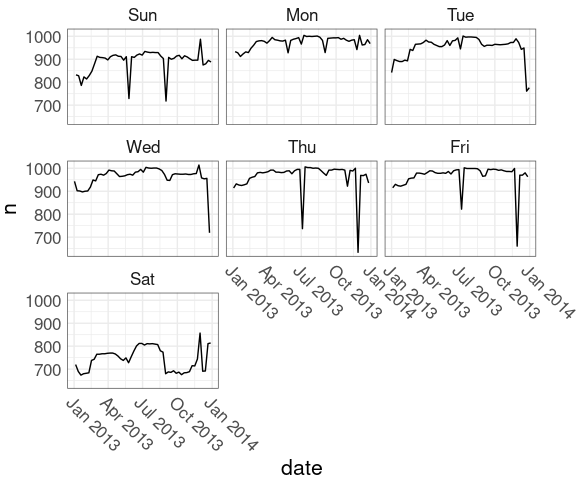
Breaking out the days of the week into separate facets may help:
nnf <-
mutate(nf, wd = wday(date, label = TRUE))
nnf_thm <-
theme(axis.text.x =
element_text(angle = -45,
hjust = 0),
plot.margin = margin(r = 30))
ggplot(nnf, aes(date, n)) +
geom_line() +
facet_wrap(~ wd) +
nnf_thmJuly 4 in 2013:
as.character(wday(ymd("2013-07-04"),
label = TRUE))
## [1] "Thu"Identifying when some major holidays occur may also be useful:
holidays <-
data.frame(Holiday = c("4th of July",
"Thanksgiving"),
date = ymd(c("2013-07-04",
"2013-11-28")))
hlayer <-
geom_vline(aes(xintercept = date,
color = Holiday),
linetype = 2,
linewidth = 1,
data = holidays)
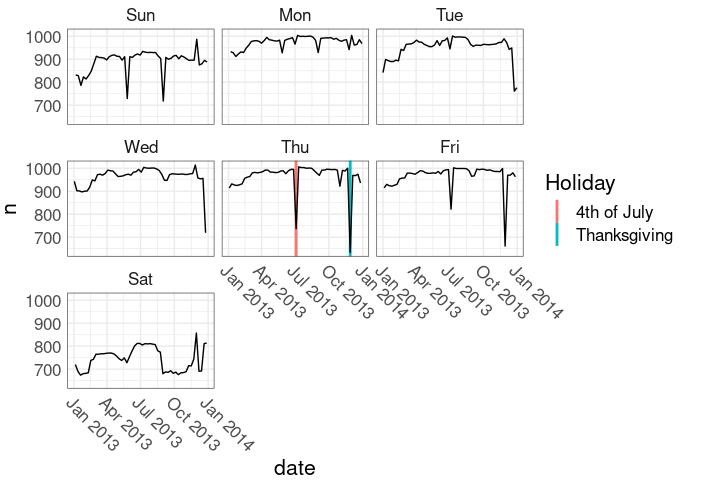
ggplot(nf, aes(date, n)) +
hlayer +
geom_line()Holidays in the faceted plot:
ggplot(nnf, aes(date, n)) +
hlayer +
geom_line() +
facet_wrap(~ wd) +
nnf_thmThis marks the holiday weeks.
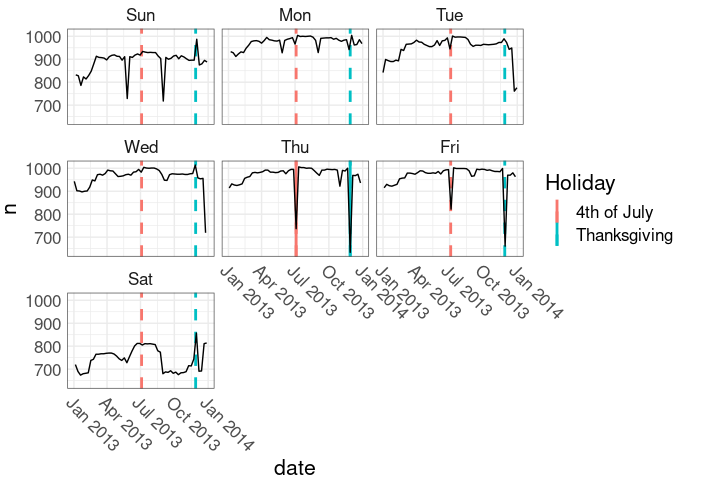
Holidays in the faceted plot:
This shows only the holiday days.
hlayer2 <-
geom_vline(aes(xintercept = date,
color = Holiday),
linewidth = 1,
data = mutate(holidays,
wd = wday(date,
TRUE)))
ggplot(nnf, aes(date, n)) +
hlayer2 +
geom_line() +
facet_wrap(~ wd) +
nnf_thmHolidays in the faceted plot:
ggplot(nnf, aes(date, n)) +
hlayer +
hlayer2 +
geom_line() +
facet_wrap(~ wd) +
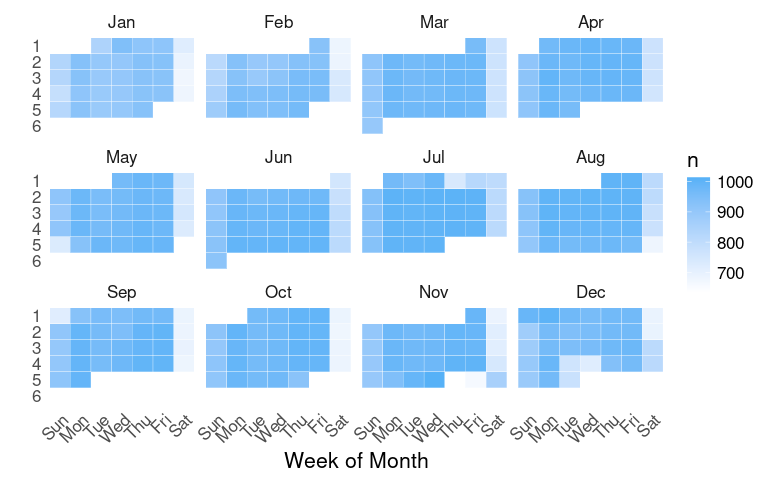
nnf_thmA simple calendar plot:
geom_tile and faceting.
monthweek <- function(d, w)
ceiling((d - w) / 7) + 1
nf <- mutate(nf,
wd = wday(date, label = TRUE),
wd = fct_rev(wd),
mw = monthweek(day, wday(date)))
p <- ggplot(nf, aes(x = as.character(mw),
y = wd,
fill = n)) +
geom_tile(color = "white") +
facet_wrap(~ month(date, label = TRUE))
pSome theme and color adjustments:
p <- p +
scale_fill_gradient(low = "white") +
ylab("") + xlab("Week of Month") +
theme(panel.grid.major = element_blank(),
panel.border = element_blank())
pThis layout with days on the vertical axis works well with a single row, which could be extended to a multi-year plot:
p + facet_wrap(~ month(date, TRUE), nrow = 1)
A more standard layout:
nf2 <-
mutate(nf,
wd = wday(date, label = TRUE),
mw = factor(monthweek(day,
wday(date))),
mw = fct_rev(mw))
wdlabs <-substr(levels(nf2$wd), 1, 1)
ggplot(nf2, aes(x = wd, y = mw, fill = n)) +
geom_tile(color = "white") +
facet_wrap(~ month(date, TRUE)) +
scale_fill_gradient(low = "white") +
xlab("") + ylab("Week of Month") +
scale_x_discrete(labels = wdlabs) +
theme(panel.grid.major = element_blank(),
panel.border = element_blank())
Exercises
A useful feature of the lattice package is the ability to easily request an aspect ratio that is banked to 45 degrees by specifying aspect = "xy" in the arguments to lattice plotting functions. For example, This code produces a reasonable aspect ratio for a plot of an unemployment time series:
library(ggplot2)
library(forecast)
library(lattice)
unemp_ts <- ts(economics$unemploy, start = c(1967, 7), frequency = 12)
xyplot(unemp_ts, aspect = "xy")
Which of the following plots most closely matches the aspect ratio in the lattice plot?
autoplot(unemp_ts, aspect = 200)autoplot(unemp_ts) + coord_fixed(ratio = 0.0007)autoplot(unemp_ts) + coord_fixed(asp = 0.0007)autoplot(unemp_ts) + coord_fixed(70)
LS0tCnRpdGxlOiAiVGltZSBTZXJpZXMgUGxvdHMiCm91dHB1dDoKICBodG1sX2RvY3VtZW50OgogICAgdG9jOiB5ZXMKICAgIGNvZGVfZm9sZGluZzogc2hvdwogICAgY29kZV9kb3dubG9hZDogdHJ1ZQotLS0KCjxsaW5rIHJlbD0ic3R5bGVzaGVldCIgaHJlZj0ic3RhdDQ1ODAuY3NzIiB0eXBlPSJ0ZXh0L2NzcyIgLz4KPHN0eWxlIHR5cGU9InRleHQvY3NzIj4gLnJlbWFyay1jb2RlIHsgZm9udC1zaXplOiA4NSU7IH0gPC9zdHlsZT4KYGBge3Igc2V0dXAsIGluY2x1ZGUgPSBGQUxTRX0Kc291cmNlKGhlcmU6OmhlcmUoInNldHVwLlIiKSkKa25pdHI6Om9wdHNfY2h1bmskc2V0KGNvbGxhcHNlID0gVFJVRSwgbWVzc2FnZSA9IEZBTFNFLAogICAgICAgICAgICAgICAgICAgICAgZmlnLmhlaWdodCA9IDUsIGZpZy53aWR0aCA9IDYsIGZpZy5hbGlnbiA9ICJjZW50ZXIiKQoKb3B0aW9ucyhodG1sdG9vbHMuZGlyLnZlcnNpb24gPSBGQUxTRSkKCnNldC5zZWVkKDEyMzQ1KQpsaWJyYXJ5KGdncGxvdDIpCmxpYnJhcnkobGF0dGljZSkKbGlicmFyeSh0aWR5dmVyc2UpCmxpYnJhcnkoZ3JpZEV4dHJhKQpsaWJyYXJ5KHBhdGNod29yaykKdGhlbWVfc2V0KHRoZW1lX21pbmltYWwoKSArCiAgICAgICAgICB0aGVtZSh0ZXh0ID0gZWxlbWVudF90ZXh0KHNpemUgPSAxNiksCiAgICAgICAgICAgICAgICBwYW5lbC5ib3JkZXIgPSBlbGVtZW50X3JlY3QoY29sb3IgPSAiZ3JleTMwIiwgZmlsbCA9IE5BKSkpCmBgYAoKCiMjIFRpbWUgU2VyaWVzIERhdGEKCkEgbG90IG9mIGRhdGEgaXMgY29sbGVjdGVkIG92ZXIgdGltZToKCi0gZWNvbm9taWMgcGVyZm9ybWFjZSBtZWFzdXJlczsKCi0gd2VhdGhlciwgY2xpbWF0ZSBkYXRhOwoKLSBtZWRpY2FsIGluZm9ybWF0aW9uLgoKVGhlIG9iamVjdGl2ZXMgY2FuIGJlCgotIHVuZGVyc3RhbmRpbmcgdGhlIHBhc3QgJm5kYXNoOyBob3cgd2UgZ290IHdoZXJlIHdlIGFyZTsKCi0gdW5kZXJzdGFuZGluZyBwYXR0ZXJucyBpbiB2YXJpYXRpb247CgotIGZvcmVjYXN0aW5nIHdoYXQgd2lsbCBoYXBwZW4gbmV4dC4KCkV2ZW4gaWYgdGltZSBpcyBub3Qgb2YgcHJpbWFyeSBpbnRlcmVzdCwgZGF0YSBhcmUgb2Z0ZW4gY29sbGVjdGVkIHdpdGgKYSB0aW1lIHN0YW1wLgoKRXhhbWluaW5nIHRoZSBiZWhhdmlvciBvdmVyIHRpbWUgY2FuIHJldmVhbCBpbnRlcmVzdGluZyBmZWF0dXJlcyB0aGF0Cm1heSBoaW50IGF0IGNvbmZvdW5kaW5nIHZhcmlhYmxlczoKCi0gdGVtcGVyYXR1cmUgdmFyeWluZyB3aXRoIHRpbWUgb2YgZGF5OwoKLSBodW1pZGl0eSB2YXJ5aW5nIG92ZXIgdGhlIHllYXIuCgpUaW1lIHNlcmllcyBkYXRhIGNhbiBiZSBjb2xsZWN0ZWQgYXQgcmVndWxhcmx5IHNwYWNlZCBpbnRlcnZhbHM6CgotIHllYXJseSwgZS5nLiB0aGUgYGdhcG1pbmRlcmAgZGF0YQoKLSBtb250aGx5LCBlLmcuIHRoZSBgcml2ZXJgIGRhdGEKCi0gZGFpbHksIGUuZy4gaGlnaCB0ZW1wZXJhdHVyZXMuCgpEYXRhIG1pZ2h0IGJlIG1pc3NpbmcKCi0gaXJyZWd1bGFybHksIGUuZy4gZmF1bHR5IGluc3RydW1lbnQsIGhvbGlkYXlzOwoKLSByZWd1bGFybHksIGUuZy4gd2Vla2VuZHMuCgpUaW1lIHNlcmllcyBjYW4gYWxzbyBiZSByZWNvcmRlZCBhdCBpcnJlZ3VsYXIgdGltZXM6CgotIGJsb29kIHByZXNzdXJlIGF0IGRvY3RvciB2aXNpdHM7CgpWYXJpYWJsZXMgcmVjb3JkZWQgb3ZlciB0aW1lIGNhbiBiZSBudW1lcmljYWwgb3IgY2F0ZWdvcmljYWwuCgoKIyMgVGltZSBTZXJpZXMgT2JqZWN0cwoKVGltZSBzZXJpZXMgZGF0YSBjYW4gYmUgcmVwcmVzZW50ZWQgYXMgcmVndWxhciBkYXRhIGZyYW1lcyB3aXRoIGEgdGltZQp2YXJpYWJsZS4KClRoZXJlIGFyZSBhbHNvIGEgbnVtYmVyIG9mIHNwZWNpYWxpemVkIG9iamVjdCBjbGFzc2VzIGZvciBkZWFsaW5nIHdpdGggdGltZQpzZXJpZXMuCgpBIG51bWJlciBvZiBwYWNrYWdlcyBwcm92aWRlIGBwbG90YCBvciBgYXV0b3Bsb3RgIG1ldGhvZHMgYW5kIG90aGVyCnV0aWxpdGllcyBmb3IgdGhlc2Ugb2JqZWN0cy4KClNvbWUgb2YgdGhlIG1vc3QgdXNlZnVsOgoKfCBDbGFzcyAgICAgIHwgIFBhY2thZ2UgICB8IEZlYXR1cmVzICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIHwKfCAtLS0tLS0tLS0tIHwgLS0tLS0tLS0tLSB8IC0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tLS0tIHwKfGB0c2AsIGBtdHNgfCBgYmFzZWAgICAgIHwgcmVndWxhciBzZXJpZXM7IG1ldGhvZHMgZm9yIGBwbG90YCBhbmQgYGxpbmVzYC4gICB8CnwgICAgICAgICAgIHwgYGZvcmVjYXN0YCB8IG1ldGhvZHMgZm9yIGBhdXRvcGxvdGAgYW5kIGBhdXRvbGF5ZXJgLiAgICAgICAgICB8Cnxgem9vYCAgICAgIHwgIGB6b29gICAgICB8IGlycmVndWxhciBhbmQgcmVndWxhciBzZXJpZXM7IGBhdXRvcGxvdGAgc3VwcG9ydC4gfAp8ICAgICAgICAgICB8IGBicm9vbWAgICAgfGB0aWR5YCBmb3IgY29udmVydGluZyB0byB0aWR5IGRhdGEgZnJhbWVzLiAgICAgICAgIHwKCgojIyBgYXV0b3Bsb3RgIGFuZCBgYXV0b2xheWVyYAoKTWFueSBkYXRhIHN0cnVjdHVyZXMgcHJvdmlkZSBtZXRob2RzIGZvciBgYXV0b3Bsb3RgIGFuZCBgYXV0b2xheWVyYC4KCkZyb20gdGhlIGBhdXRvcGxvdGAgaGVscCBwYWdlOgoKPiBgYXV0b3Bsb3RgIHVzZXMgYGdncGxvdDJgIHRvIGRyYXcgYSBwYXJ0aWN1bGFyIHBsb3QgZm9yIGFuIG9iamVjdCBvZgo+IGEgcGFydGljdWxhciBjbGFzcyBpbiBhIHNpbmdsZSBjb21tYW5kLiBUaGlzIGRlZmluZXMgdGhlIFMzIGdlbmVyaWMKPiB0aGF0IG90aGVyIGNsYXNzZXMgYW5kIHBhY2thZ2VzIGNhbiBleHRlbmQuCgpGcm9tIHRoZSBgYXV0b2xheWVyYCBoZWxwIHBhZ2U6Cgo+IGBhdXRvbGF5ZXJgIHVzZXMgYGdncGxvdDJgIHRvIGRyYXcgYSBwYXJ0aWN1bGFyIGxheWVyIGZvciBhbiBvYmplY3QKPiBvZiBhIHBhcnRpY3VsYXIgY2xhc3MgaW4gYSBzaW5nbGUgY29tbWFuZC4gVGhpcyBkZWZpbmVzIHRoZSBTMwo+IGdlbmVyaWMgdGhhdCBvdGhlciBjbGFzc2VzIGFuZCBwYWNrYWdlcyBjYW4gZXh0ZW5kLgoKCiMjIEV4YW1wbGU6IFJpdmVyIERhdGEKCkNyZWF0aW5nIGEgYHRzYCBvYmplY3QgZm9yIHRoZSBgcml2ZXJgIGRhdGE6CgpgYGB7ciwgaW5jbHVkZSA9IEZBTFNFfQpvcCA8LSBvcHRpb25zKG1heC5wcmludCA9IDEyKQpgYGAKYGBge3J9CnJpdmVyIDwtIHNjYW4oImh0dHBzOi8vd3d3LnN0YXQudWlvd2EuZWR1L35sdWtlL2RhdGEvcml2ZXIuZGF0IikKKHJpdmVyVFMgPC0gdHMocml2ZXIpKQpgYGAKCk9yLCBzaW5jZSB0aGUgZGF0YSB3ZXJlIGNvbGxlY3RlZCBtb250aGx5OgoKYGBge3J9CihyaXZlclRTIDwtIHRzKHJpdmVyLCBmcmVxdWVuY3kgPSAxMikpCmBgYApgYGB7ciwgaW5jbHVkZSA9IEZBTFNFfQpvcHRpb25zKG9wKQpgYGAKClVzaW5nIGB0aWR5YCBmcm9tIHBhY2thZ2UgYGJyb29tYCB0byBjcmVhdGUgYSBkYXRhIGZyYW1lIGZyb20gdGhlIGB0c2Agb2JqZWN0OgoKYGBge3J9CnJpdmVyREYgPC0gYnJvb206OnRpZHkocml2ZXJUUykKaGVhZChyaXZlckRGLCAzKQpgYGAKCkNoYW5nZSB0byBtb3JlIGNvbnZlbmllbnQgbmFtZXM6CgpgYGB7cn0Kcml2ZXJERiA8LSByZW5hbWUocml2ZXJERiwgdGltZSA9IGluZGV4LCBmbG93ID0gdmFsdWUpCmhlYWQocml2ZXJERiwgMykKYGBgCgoKIyMgQmFzaWMgUGxvdHMgZm9yIGEgU2luZ2xlIE51bWVyaWMgVGltZSBTZXJpZXMKCk51bWVyaWMgdGltZSBzZXJpZXMgYXJlIHVzdWFsbHkgcGxvdHRlZCBhcyBhIF9saW5lIGNoYXJ0Xy4KClRoaXMgaXMgd2hhdCB0aGUgYGF1dG9wbG90YCBtZXRob2QgZm9yIGB0c2Agb2JqZWN0cyBwcm92aWRlZCBieQpwYWNrYWdlIGBmb3JlY2FzdGAgZG9lcy4KCkZvciB0aGUgcml2ZXIgZmxvdyBkYXRhOgoKYGBge3Igcml2ZXItdHMtYXV0b3Bsb3QsIGVjaG8gPSBGQUxTRX0KbGlicmFyeShmb3JlY2FzdCkKcCA8LSBhdXRvcGxvdChyaXZlclRTKQpwCmBgYAoKYGBge3Igcml2ZXItdHMtYXV0b3Bsb3QsIGV2YWwgPSBGQUxTRX0KYGBgCgpVc2luZyBzeW1ib2xzIGluIGFkZGl0aW9uIHRvIGxpbmVzIGlzIHNvbWV0aW1lcyB1c2VmdWw6CgpgYGB7ciByaXZlci10cy1hdXRvcGxvdC1zeW1zLCBlY2hvID0gRkFMU0V9CnAgKyBnZW9tX3BvaW50KCkKYGBgCgpgYGB7ciByaXZlci10cy1hdXRvcGxvdC1zeW1zLCBldmFsID0gRkFMU0V9CmBgYAoKCiMjIEFzcGVjdCBSYXRpbwoKQXNwZWN0IHJhdGlvIGhhcyBhIHNpZ25pZmljYW50IGVmZmVjdCBvbiBob3cgd2VsbCB3ZSBwZXJjZWl2ZSBzbG9wZQpkaWZmZXJlbmNlcy4KCi0gQmFua2luZyB0byA0NSBkZWdyZWVzOiBjaG9vc2UgYW4gYXNwZWN0IHJhdGlvIHNvIHRoZSBtYWduaXR1ZGUgb2YKICB0aGUgaW1wb3J0YW50IHNsb3BlcyBpcyBjbG9zZSB0byA0NSBkZWdyZWVzLgoKLSBUaGlzIHVzdWFsbHkgcmVxdWlyZXMgdGhlIGhvcml6b250YWwgYXhpcyB0byBiZSBsb25nZXIgdGhhbiB0aGUKICB2ZXJ0aWNhbCBheGlzLgoKQ29udHJvbGxpbmcgdGhlIGFzcGVjdCByYXRpbzoKCi0gRm9yIGBiYXNlYCBncmFwaGljcyB1c2UgdGhlIGBhc3BgIGFyZ3VtZW50IHRvIGBwbG90YC4KCi0gYGxhdHRpY2VgIHVzZXMgdGhlIGBhc3BlY3RgIGFyZ3VtZW50LgoKLSBGb3IgYGdncGxvdGAgdXNlIHRoZSBgcmF0aW9gIGFyZ3VtZW50IHRvIGBjb29yZF9maXhlZGAuCgpgYGB7ciwgZmlnLmhlaWdodCA9IDMsIGZpZy53aWR0aCA9IDEwfQpwICsgY29vcmRfZml4ZWQocmF0aW8gPSAxIC8gMykKYGBgCgpMYXR0aWNlIHN1cHBvcnRzIHNldmVyYWwgYXNwZWN0IHJhdGlvIHN0cmF0ZWdpZXM6CgotIGAiZmlsbCJgIHRvIGF2b2lkIHVudXNlZCB3aGl0ZSBzcGFjZTsKCi0gYCJ4eSJgIHRvIHVzZSBhIDQ1IGRlZ3JlZSBiYW5raW5nIHJ1bGU7CgotIGAiaXNvImAgZm9yIGlzb21ldHJpYyBzY2FsZXMsIGUuZy4gZGlzdGFuY2VzLgoKU29tZSB3b3JrIG1heSBiZSBuZWVkZWQgdG8gYXZvaWQgZXhjZXNzIHdoaXRlIHNwYWNlIGFyb3VuZCBmaWd1cmVzLgoKVXNpbmcgbXVsdGlwbGUgcGFuZWxzIGNhbiBoZWxwLgoKSW4gYW4gaW50ZXJhY3RpdmUgc2V0dGluZywgem9vbSBhbmQgcGFuIHN1cHBvcnQgY2FuIGhlbHAuCgpNdWx0aXBsZSBwYW5lbHM6CgpgYGB7ciByaXZlci10cy1wYW5lbHMsIGVjaG8gPSBGQUxTRX0KbXV0YXRlKHJpdmVyREYsCiAgICAgICBwZXJpb2QgPSBjdXQodGltZSwgYnJlYWtzID0gMykpIHw+CiAgICBnZ3Bsb3QoYWVzKHRpbWUsIGZsb3cpKSArCiAgICBnZW9tX2xpbmUoKSArCiAgICBmYWNldF93cmFwKH4gcGVyaW9kLAogICAgICAgICAgICAgICBzY2FsZXMgPSAiZnJlZV94IiwKICAgICAgICAgICAgICAgbmNvbCA9IDEpCmBgYAoKYGBge3Igcml2ZXItdHMtcGFuZWxzLCBldmFsID0gRkFMU0V9CmBgYAoKQWRkaW5nIHpvb20gYW5kIHBhbiBzdXBwb3J0IHVzaW5nIFtgcGxvdGx5YF0oaHR0cHM6Ly9wbG90bHkuY29tL3IvKToKCmBgYHtyLCBpbmNsdWRlID0gRkFMU0V9CmxpYnJhcnkocGxvdGx5KQpgYGAKYGBge3IsICwgZmlnLmhlaWdodCA9IDQsIGZpZy53aWR0aCA9IDEwfQpsaWJyYXJ5KHBsb3RseSkKcHAgPC0gcCArIGdlb21fbGluZSgpICsgY29vcmRfZml4ZWQocmF0aW8gPSAxIC8gMykKZ2dwbG90bHkocHApCmBgYAoKVGhlcmUgaXMgbm90IGFsd2F5cyBhIHNpbmdsZSBiZXN0IGFzcGVjdCByYXRpby4KClRoZSBgY28yYCBkYXRhIHNldCBpbiB0aGUgYGRhdGFzZXRzYCBwYWNrYWdlIGNvbnRhaW5zIG1vbnRobHkKY29uY2VudHJhdGlvbnMgb2YgQ08yIGZvciB0aGUgeWVhcnMgMTk1OSB0byAxOTk3IHJlY29yZGVkIGF0IHRoZSBNYXVuYQpMb2Egb2JzZXJ2YXRvcnkuCgpUaGUgYGNvMmAgZGF0YSBpcyBzdG9yZWQgYXMgYW4gb2JqZWN0IG9mIGNsYXNzIGB0c2A6CmBgYHtyfQpzdHIoY28yKQpgYGAKCmBwbG90YCBhbmQgYHh5cGxvdGAgaGF2ZSBtZXRob2RzIGZvciBgdHNgIG9iamVjdHMgdGhhdCBzaW1wbGlmeSB0aW1lCnNlcmllcyBwbG90dGluZy4KClR3byBhc3BlY3QgcmF0aW9zOgoKYGBge3IgLCBmaWcuaGVpZ2h0ID0gNC41LCBmaWcud2lkdGggPSA1LjV9Cnh5cGxvdChjbzIpCmBgYAoKYGBge3IsIGZpZy5oZWlnaHQgPSA0LCBmaWcud2lkdGggPSAxMH0KeHlwbG90KGNvMiwgYXNwZWN0ID0gInh5IikKYGBgCklzIHRoZXJlIGEgc2xvd2Rvd24gaW4gdGhlIGluY3JlYXNlPwoKQSBncmFwaCB3aXRoIG1vcmUgcmVjZW50IGRhdGEgaXMKW2F2YWlsYWJsZV0oaHR0cHM6Ly9nbWwubm9hYS5nb3YvY2NnZy90cmVuZHMvKS4KClRoZSBmdWxsIGRhdGEgaXMKW2F2YWlsYWJsZV0oaHR0cHM6Ly9nbWwubm9hYS5nb3Yvd2ViZGF0YS9jY2dnL3RyZW5kcy9jbzIvY28yX2Fubm1lYW5fbWxvLnR4dCkKYXMgd2VsbC4KCmBhdXRvcGxvdGAgZG9lcyBub3QgeWV0IHByb3ZpZGUgYW4gZWFzeSB3YXkgdG8gYmFuayB0byA0NSBkZWdyZWVzOyB5b3UKbmVlZCB0byBleHBlcmltZW50IG9yIGNhbGN1bGF0ZSBhbiBhcHByb3ByaWF0ZSBhc3BlY3QgcmF0aW8geW91cnNlbGYuCgpUaGUgZGVmYXVsdCBgYXV0b3Bsb3RgOgoKYGBge3IgY28yLWF1dG9wbG90LWRlZmF1bHQsIGVjaG8gPSBGQUxTRX0KbGlicmFyeShmb3JlY2FzdCkKYXV0b3Bsb3QoY28yKQpgYGAKCmBgYHtyIGNvMi1hdXRvcGxvdC1kZWZhdWx0LCBldmFsID0gRkFMU0V9CmBgYAoKQXNwZWN0IHJhdGlvIGFkanVzdGVkIHdpdGggYGNvb3JkX2ZpeGVkYDoKCmBgYHtyLCBmaWcuaGVpZ2h0ID0gNCwgZmlnLndpZHRoID0gMTB9CnI0NSA8LSBtZWRpYW4oZGlmZih0aW1lKGNvMikpKSAvIG1lZGlhbihhYnMoZGlmZihjbzIpKSkKYXV0b3Bsb3QoY28yKSArIGNvb3JkX2ZpeGVkKHJhdGlvID0gcjQ1KQpgYGAgCgoKIyMgVXBkYXRlZCBNYXVuYSBMb2EgQ08yIERhdGEKCkRvd25sb2FkaW5nIGFuZCByZWFkaW5nIGluIHRoZSBkYXRhOgoKYGBge3IsIG1lc3NhZ2UgPSBGQUxTRX0KbGlicmFyeShsdWJyaWRhdGUpCnVybCA8LSAiaHR0cHM6Ly9nbWwubm9hYS5nb3Yvd2ViZGF0YS9jY2dnL3RyZW5kcy9jbzIvY28yX21tX21sby50eHQiCmlmICghIGZpbGUuZXhpc3RzKCJjbzJuZXcuZGF0IikgfHwKICAgIG5vdygpID4gZmlsZS5tdGltZSgiY28ybmV3LmRhdCIpICsgd2Vla3MoNCkpCiAgICBkb3dubG9hZC5maWxlKHVybCwgImNvMm5ldy5kYXQiKQpjbzJuZXcgPC0gcmVhZC50YWJsZSgiY28ybmV3LmRhdCIpCmBgYAoKQ2xlYW4gdXAgdGhlIHZhcmlhYmxlIG5hbWVzOgpgYGB7cn0KaGVhZChjbzJuZXcpCm5hbWVzKGNvMm5ldykgPC0gYygieWVhciIsICJtb250aCIsICJkZWNpbWFsX2RhdGUiLCAiYXZlcmFnZSIsCiAgICAgICAgICAgICAgICAgICAiZGVzZWFzb24iLCAibmRheXMiLCAic3RkZCIsICJ1bW0iKQpgYGAKCkFuIGluaXRpYWwgbG9vazoKCmBgYHtyfQpnZ3Bsb3QoY28ybmV3LCBhZXMoZGVjaW1hbF9kYXRlLCBhdmVyYWdlKSkgKyBnZW9tX2xpbmUoKQpgYGAKCk1pc3NpbmcgdmFsdWVzIGFyZSBlbmNvZGVkIGFzIGAtOS45OWAgb3IgYC05OS45OWAuCgpJZiB0aGVyZSBhcmUgYW55IHN1Y2ggdmFsdWVzIHRoZXkgbmVlZCB0byBiZSByZXBsYWNlZCB3aXRoIFIncyBtaXNzaW5nCnZhbHVlIHJlcHJlc2VudGF0aW9uOgoKYGBge3J9CmZpbHRlcihjbzJuZXcsIGF2ZXJhZ2UgPCAtOSkKY28ybmV3IDwtIG11dGF0ZShjbzJuZXcsIGF2ZXJhZ2UgPSBpZmVsc2UoYXZlcmFnZSA8IC05LCBOQSwgYXZlcmFnZSkpCmBgYAoKVGhpcyBwcm9kdWNlcyBhIHJlYXNvbmFibGUgcGxvdDoKCmBgYHtyLCBjbGFzcy5zb3VyY2UgPSAiZm9sZC1oaWRlIn0KZ2dwbG90KGNvMm5ldywgYWVzKGRlY2ltYWxfZGF0ZSwgYXZlcmFnZSkpICsKICAgIGdlb21fbGluZSgpCmBgYAoKVGhlIHBsb3Qgd291bGQgc2hvdyBnYXBzIGZvciB0aGUgbWlzc2luZyB2YWx1ZXMuCgpNaXNzaW5nIHZhbHVlcyBjb3VsZCBhbHNvIGJlIGludGVycG9sYXRlZCB3aXRoIGBuYS5pbnRlcnBgIGZyb20KcGFja2FnZSBgZm9yZWNhc3RgLgoKQ29udmVydGluZyB0aGUgbmV3IGRhdGEgdG8gYSBgdHNgIG9iamVjdCBtYWtlcyBhZGRpbmcgdGhlIG9yaWdpbmFsCmRhdGEgYSBsaXR0bGUgZWFzaWVyOgoKYGBge3J9CmNvMm5ld1RTIDwtIHRzKGNvMm5ldyRhdmVyYWdlLCBzdGFydCA9IGMoMTk1OCwgMyksIGZyZXF1ZW5jeSA9IDEyKQphdXRvcGxvdChjbzJuZXdUUykgKyBhdXRvbGF5ZXIoY28yKQpgYGAKCgojIyBTZWFzb25hbCBEZWNvbXBvc2l0aW9uIG9mIFRpbWUgU2VyaWVzIGJ5IExvZXNzIChTVEwpCgpGb3IgdGltZSBzZXJpZXMgd2l0aCBhIHN0cm9uZyBzZWFzb25hbCBjb21wb25lbnQgaXQgY2FuIGJlIHVzZWZ1bCB0bwpsb29rIGF0IGEgX1NlYXNvbmFsIERlY29tcG9zaXRpb24gb2YgVGltZSBTZXJpZXMgYnkgTG9lc3NfLCBvcgooX1NUTF8pLgoKVGhlIG1ldGhvZG9sb2d5IHdhcyBzdWdnZXN0ZWQgYnkgQ2xldmFsYW5kIGFuZCBjb3dvcmtlcnMuCgpUaGUgYHN0bGAgZnVuY3Rpb24gaW4gdGhlIGBiYXNlYCBwYWNrYWdlIGNvbXB1dGVzIHN1Y2ggYQpkZWNvbXBvc2l0aW9uLgoKSXQgcmVxdWlyZXMgYSBzZXJpZXMgd2l0aG91dCBtaXNzaW5nIHZhbHVlcy4KCmBgYHtyfQpjbzJuZXdUU19ub19OQSA8LSB0cyhjbzJuZXckYXZlcmFnZSwgc3RhcnQgPSBjKDE5NTgsIDMpLCBmcmVxdWVuY3kgPSAxMikKY28yc3RsIDwtIHN0bChjbzJuZXdUU19ub19OQSwgcy53aW5kb3cgPSAyMSkKaGVhZChjbzJzdGwkdGltZS5zZXJpZXMpCmBgYAoKUGFja2FnZSBgZm9yZWNhc3RgIHByb3ZpZGVzIGFuIGBhdXRvcGxvdGAgbWV0aG9kIGZvciBgc3RsYCBvYmplY3RzIHRoYXQKc2hvd3MgdGhlIG9yaWdpbmFsIGRhdGEgYW5kIHRoZSB0aHJlZSBjb21wb25lbnRzIGluIHNlcGFyYXRlIHBhbmVsczoKCmBgYHtyIGNvMi1zdGwtcGxvdCwgZXZhbCA9IEZBTFNFfQphdXRvcGxvdChjbzJzdGwpCmBgYAoKYGBge3IgY28yLXN0bC1wbG90LCBlY2hvID0gRkFMU0UsIGZpZy5oZWlnaHQgPSA3fQpgYGAKCgojIyBTb21lIEFsdGVybmF0aXZlIFZpc3VhbGl6YXRpb25zCgpCYXIgY2hhcnRzIGFyZSBzb21ldGltZXMgdXNlZCB3aGVuIGNvbXBhcmlzb24gdG8gYSBiYXNlIGxpbmUgaXMKaW1wb3J0YW50OyBmb3IgZXhhbXBsZSBmb3IgW2lsbHVzdHJhdGluZyBjbGltYXRlCmNoYW5nZV0oYHIgSU1HKCJDYUdfR2xvYmFsVGVtcEFub21fMS5qcGciKWApLiAgPCEtLSBvcmlnaW5hbCBhdApodHRwczovL3d3dy5jbGltYXRlLmdvdi9zaXRlcy9kZWZhdWx0L2ZpbGVzL0NhR19HbG9iYWxUZW1wQW5vbV8xLmpwZwpEYXRhIGlzIGF2YWlsYWJsZSBmcm9tCmh0dHBzOi8vd3d3LmNsaW1hdGUuZ292L21hcHMtZGF0YS9kYXRhc2V0L2dsb2JhbC10ZW1wZXJhdHVyZS1hbm9tYWxpZXMtZ3JhcGhpbmctdG9vbAotLT4KCkNhbGVuZGFyIHBsb3RzLCBvciBjYWxlbmRhciBoZWF0bWFwcywgYXJlIHNvbWV0aW1lcyB1c2VmdWwgZm9yCmRpc3BsYXlpbmcgZGFpbHkgZGF0YSB3aGVyZSBkYXkgb2YgdGhlIHdlZWsvd2Vla2VuZCBlZmZlY3RzIG1pZ2h0IGJlCmltcG9ydGFudC4gIE9uZSBleGFtcGxlIGlzIGF2YWlsYWJsZSBbaGVyZV0oYHIgSU1HKCJjYWxlbmRhckhlYXRtYXAucG5nIilgKS4KCkEgW2Jsb2cgcG9zdF0oaHR0cHM6Ly9kb21pbmlra29jaC5naXRodWIuaW8vQ2FsZW5kYXItSGVhdG1hcC8pIHNob3dzCmhvdyB0byBidWlsZCBhIGNhbGVuZGFyIHBsb3Qgd2l0aCBgZ2dwbG90YC4KCgojIyBHRFAgR3Jvd3RoIERhdGEKCkJhciBjaGFydHMgYXJlIHNvbWV0aW1lcyB1c2VkIGZvciBlY29ub21pYyB0aW1lIHNlcmllcywgaW4gcGFydGljdWxhcgpncm93dGggcmF0ZSBkYXRhLgoKU29tZSBHRFAgZ3Jvd3RoIHJhdGUgZGF0YSBpcyBhdmFpbGFibGUgb24gdGhpcwpbd2ViIHBhZ2VdKGh0dHBzOi8vd3d3Lm11bHRwbC5jb20vdXMtcmVhbC1nZHAtZ3Jvd3RoLXJhdGUvdGFibGUvYnktcXVhcnRlcik6CgpSZWFkIHRoZSBkYXRhIGZyb20gdGhlIHdlYiBwYWdlOgoKYGBge3IsIGNhY2hlID0gVFJVRX0KbGlicmFyeShydmVzdCkKZ2RwdXJsIDwtICJodHRwOi8vd3d3Lm11bHRwbC5jb20vdXMtcmVhbC1nZHAtZ3Jvd3RoLXJhdGUvdGFibGUvYnktcXVhcnRlciIKZ2RwcGFnZSA8LSByZWFkX2h0bWwoZ2RwdXJsKQpnZHB0YmwgPC0gaHRtbF90YWJsZShnZHBwYWdlKVtbMV1dCmhlYWQoZ2RwdGJsKQpgYGAKCkNsZWFuIHRoZSBkYXRhOgoKYGBge3IsIG1lc3NhZ2UgPSBGQUxTRX0KbGlicmFyeShkcGx5cikKbGlicmFyeShsdWJyaWRhdGUpCm5hbWVzKGdkcHRibCkgPC0gYygiRGF0ZSIsICJWYWx1ZSIpCmdkcHRibCA8LSBtdXRhdGUoZ2RwdGJsLAogICAgICAgICAgICAgICAgIFZhbHVlID0gYXMubnVtZXJpYyhzdWIoIiUiLCAiIiwgVmFsdWUpKSwKICAgICAgICAgICAgICAgICBEYXRlID0gbWR5KERhdGUpKQpoZWFkKGdkcHRibCkKYGBgCgpEYXRhIHByaW9yIHRvIDE5NDcgaXMgYW5udWFsLCBzbyBkcm9wIGVhcmxpZXIgZGF0YToKCmBgYHtyfQpnZHB0YmwgPC0gZmlsdGVyKGdkcHRibCwKICAgICAgICAgICAgICAgICBEYXRlID49IG1ha2VfZGF0ZSgxOTQ4LCAxLCAxKSkKYGBgCgpSZWFycmFuZ2UgdG8gcHV0IGBEYXRlYCBpbiBpbmNyZWFzaW5nIG9yZGVyOgoKYGBge3J9CmdkcHRibCA8LSBhcnJhbmdlKGdkcHRibCwgRGF0ZSkKYGBgCgpDcmVhdGUgYW5kIHBsb3QgYSB0aW1lIHNlcmllczoKCmBgYHtyIGdkcC1wbG90LCBldmFsID0gRkFMU0V9CmxpYnJhcnkoZ2dwbG90MikKbGlicmFyeShmb3JlY2FzdCkKZ2RwdHMgPC0gdHMoZ2RwdGJsJFZhbHVlLAogICAgICAgICAgICBzdGFydCA9IDE5NDgsIGZyZXF1ZW5jeSA9IDQpCmF1dG9wbG90KGdkcHRzKSArCiAgICBnZW9tX2hsaW5lKHlpbnRlcmNlcHQgPSAwLCBsaW5ldHlwZSA9IDIpCmBgYAoKYGBge3IgZ2RwLXBsb3QsIGVjaG8gPSBGQUxTRX0KYGBgCgpBIGJhciBjaGFydCB3aXRoIGNvbG9yIHVzZWQgdG8gZGlzdGluZ3Vpc2ggcG9zaXRpdmUgYW5kIG5lZ2F0aXZlCmdyb3d0aCBjYW4gYmUgY3JlYXRlZCBmcm9tIHRoZSBvcmlnaW5hbCB0YWJsZSBgZ2RwdGJsYDoKCmBgYHtyIGdkcC1iYXIsIGV2YWwgPSBGQUxTRSwgZGV2ID0gInN2ZyJ9CmxpYnJhcnkoZ2dwbG90MikKbXV0YXRlKGdkcHRibCwKICAgICAgIGdyb3d0aCA9IGlmZWxzZShWYWx1ZSA+PSAwLAogICAgICAgICAgICAgICAgICAgICAgICJwb3MiLAogICAgICAgICAgICAgICAgICAgICAgICJuZWciKSkgfD4KICAgIGdncGxvdChhZXMoeCA9IERhdGUsCiAgICAgICAgICAgICAgIHkgPSBWYWx1ZSwKICAgICAgICAgICAgICAgZmlsbCA9IGdyb3d0aCkpICsKICAgIGdlb21fY29sKCkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKAogICAgICAgIHZhbHVlcyA9IGMocG9zID0gImJsdWUiLCBuZWcgPSAicmVkIikpCmBgYAoKYGBge3IgZ2RwLWJhciwgZWNobyA9IEZBTFNFfQpgYGAKClRoZSBiYXIgY2hhcnQgY2FuIGFsc28gYmUgY3JlYXRlZCBmcm9tIHRoZSB0aW1lIHNlcmllcyBvYmplY3Q6CgpgYGB7ciBnZHAtYmFyLXRzLCBldmFsID0gRkFMU0UsIGRldiA9ICJzdmcifQpkYXRhLmZyYW1lKHJhdGUgPSBhcy5udW1lcmljKGdkcHRzKSwKICAgICAgICAgICB0aW1lID0gYXMubnVtZXJpYyh0aW1lKGdkcHRzKSkpIHw+CiAgICBtdXRhdGUoZ3Jvd3RoID0gaWZlbHNlKHJhdGUgPj0gMCwKICAgICAgICAgICAgICAgICAgICAgICAgICAgInBvcyIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICJuZWciKSkgfD4KICAgIGdncGxvdChhZXModGltZSwgcmF0ZSwgZmlsbCA9IGdyb3d0aCkpICsKICAgIGdlb21fY29sKCkgKwogICAgdGhlbWUobGVnZW5kLnBvc2l0aW9uID0gInRvcCIpICsKICAgIHNjYWxlX2ZpbGxfbWFudWFsKAogICAgICAgIHZhbHVlcyA9IGMocG9zID0gImJsdWUiLCBuZWcgPSAicmVkIikpCmBgYAoKYGBge3IgZ2RwLWJhci10cywgZWNobyA9IEZBTFNFfQpgYGAKCgojIyBBaXJsaW5lIEZsaWdodHMgRnJvbSBOWUMKClRoZSBgbnljZmxpZ2h0czEzYCBkYXRhIHNldCBjb250YWlucyBkYXRhIG9uIGFsbCBmbGlnaHQgbGVhdmluZyBOZXcKWW9yayBDaXR5IGluIDIwMTMuCgpTaW1pbGFyIGRhdGEgaXMgYXZhaWxhYmxlIGZvciBvdGhlciBjaXRpZXMgYW5kIHllYXJzLCBlLmcuIGZyb20gdGhlCltgYW55ZmxpZ2h0c2AgcGFja2FnZV0oaHR0cHM6Ly9zaW1vbnBjb3VjaC5naXRodWIuaW8vYW55ZmxpZ2h0cy8pLgoKV2UgY2FuIGxvb2sgYXQgdGhlIG51bWJlciBvZiBkZXBhcnR1cmVzIGZvciBlYWNoIGRheToKCmBgYHtyfQpsaWJyYXJ5KG55Y2ZsaWdodHMxMykKbGlicmFyeShnZ3Bsb3QyKQpuZiA8LSBjb3VudChmbGlnaHRzLCB5ZWFyLCBtb250aCwgZGF5KQpgYGAKCkl0IHdpbGwgYmUgdXNlZnVsIHRvIGhhdmUgYSBjb21iaW5lZCBgZGF0ZWAgZmllbGQgaW4gb3VyIGRhdGEgZnJhbWUuCgpUaGUgYGx1YnJpZGF0ZWAgZnVuY3Rpb24gYG1ha2VfZGF0ZWAgY2FuIGJlIHVzZWQgZm9yIHRoaXM6CgpgYGB7cn0KbGlicmFyeShsdWJyaWRhdGUpCm5mIDwtIG11dGF0ZShuZiwgZGF0ZSA9IG1ha2VfZGF0ZSh5ZWFyLCBtb250aCwgZGF5KSkKYGBgCgpBIGxpbmUgcGxvdCBvZiB0aGUgbnVtYmVyIG9mIGZsaWdodHM6CgpgYGB7ciBmbGlnaHRzLTEsIGVjaG8gPSBGQUxTRX0KZ2dwbG90KG5mLCBhZXMoZGF0ZSwgbikpICsKICAgIGdlb21fbGluZSgpCmBgYApgYGB7ciBmbGlnaHRzLTEsIGV2YWwgPSBGQUxTRX0KYGBgCgpXZWVrZGF5IHZhcmlhdGlvbiBpcyBjbGVhcmx5IHZpc2libGUuCgpCcmVha2luZyBvdXQgdGhlIGRheXMgb2YgdGhlIHdlZWsgaW50byBzZXBhcmF0ZSBmYWNldHMgbWF5IGhlbHA6CgpgYGB7ciBmbGlnaHRzLTIsIGVjaG8gPSBGQUxTRX0Kbm5mIDwtCiAgICBtdXRhdGUobmYsIHdkID0gd2RheShkYXRlLCBsYWJlbCA9IFRSVUUpKQoKbm5mX3RobSA8LQogICAgdGhlbWUoYXhpcy50ZXh0LnggPQogICAgICAgICAgICAgIGVsZW1lbnRfdGV4dChhbmdsZSA9IC00NSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgaGp1c3QgPSAwKSwKICAgICAgICAgIHBsb3QubWFyZ2luID0gbWFyZ2luKHIgPSAzMCkpCgpnZ3Bsb3Qobm5mLCBhZXMoZGF0ZSwgbikpICsKICAgIGdlb21fbGluZSgpICsKICAgIGZhY2V0X3dyYXAofiB3ZCkgKwogICAgbm5mX3RobQpgYGAKCmBgYHtyIGZsaWdodHMtMiwgZXZhbCA9IEZBTFNFfQpgYGAKCkp1bHkgNCBpbiAyMDEzOgoKYGBge3J9CmFzLmNoYXJhY3Rlcih3ZGF5KHltZCgiMjAxMy0wNy0wNCIpLAogICAgICAgICAgICAgICAgICBsYWJlbCA9IFRSVUUpKQpgYGAKCklkZW50aWZ5aW5nIHdoZW4gc29tZSBtYWpvciBob2xpZGF5cyBvY2N1ciBtYXkgYWxzbyBiZSB1c2VmdWw6CgpgYGB7ciBmbGlnaHRzLTMsIGVjaG8gPSBGQUxTRSwgZmlnLndpZHRoID0gNy41fQpob2xpZGF5cyA8LQogICAgZGF0YS5mcmFtZShIb2xpZGF5ID0gYygiNHRoIG9mIEp1bHkiLAogICAgICAgICAgICAgICAgICAgICAgICAgICAiVGhhbmtzZ2l2aW5nIiksCiAgICAgICAgICAgICAgIGRhdGUgPSB5bWQoYygiMjAxMy0wNy0wNCIsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAiMjAxMy0xMS0yOCIpKSkKaGxheWVyIDwtCiAgICBnZW9tX3ZsaW5lKGFlcyh4aW50ZXJjZXB0ID0gZGF0ZSwKICAgICAgICAgICAgICAgICAgIGNvbG9yID0gSG9saWRheSksCiAgICAgICAgICAgICAgIGxpbmV0eXBlID0gMiwKICAgICAgICAgICAgICAgbGluZXdpZHRoID0gMSwKICAgICAgICAgICAgICAgZGF0YSA9IGhvbGlkYXlzKQpnZ3Bsb3QobmYsIGFlcyhkYXRlLCBuKSkgKwogICAgaGxheWVyICsKICAgIGdlb21fbGluZSgpCmBgYApgYGB7ciBmbGlnaHRzLTMsIGV2YWwgPSBGQUxTRX0KYGBgCgpIb2xpZGF5cyBpbiB0aGUgZmFjZXRlZCBwbG90OgoKYGBge3IgZmxpZ2h0cy1ob2xpZGF5LWZhY2V0LTEsIGVjaG8gPSBGQUxTRSwgZmlnLndpZHRoID0gNy41fQpnZ3Bsb3Qobm5mLCBhZXMoZGF0ZSwgbikpICsKICAgIGhsYXllciArCiAgICBnZW9tX2xpbmUoKSArCiAgICBmYWNldF93cmFwKH4gd2QpICsKICAgIG5uZl90aG0KYGBgCgpgYGB7ciBmbGlnaHRzLWhvbGlkYXktZmFjZXQtMSwgZXZhbCA9IEZBTFNFfQpgYGAKClRoaXMgbWFya3MgdGhlIGhvbGlkYXkgd2Vla3MuCgpIb2xpZGF5cyBpbiB0aGUgZmFjZXRlZCBwbG90OgoKYGBge3IgZmxpZ2h0cy1ob2xpZGF5LWZhY2V0LTIsIGVjaG8gPSBGQUxTRSwgZmlnLndpZHRoID0gNy41fQpobGF5ZXIyIDwtCiAgICBnZW9tX3ZsaW5lKGFlcyh4aW50ZXJjZXB0ID0gZGF0ZSwKICAgICAgICAgICAgICAgICAgIGNvbG9yID0gSG9saWRheSksCiAgICAgICAgICAgICAgIGxpbmV3aWR0aCA9IDEsCiAgICAgICAgICAgICAgIGRhdGEgPSBtdXRhdGUoaG9saWRheXMsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgd2QgPSB3ZGF5KGRhdGUsCiAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgIFRSVUUpKSkKZ2dwbG90KG5uZiwgYWVzKGRhdGUsIG4pKSArCiAgICBobGF5ZXIyICsKICAgIGdlb21fbGluZSgpICsKICAgIGZhY2V0X3dyYXAofiB3ZCkgKwogICAgbm5mX3RobQpgYGAKClRoaXMgc2hvd3Mgb25seSB0aGUgaG9saWRheSBkYXlzLgoKYGBge3IgZmxpZ2h0cy1ob2xpZGF5LWZhY2V0LTIsIGV2YWwgPSBGQUxTRX0KYGBgCgpIb2xpZGF5cyBpbiB0aGUgZmFjZXRlZCBwbG90OgoKYGBge3IgZmxpZ2h0cy1ob2xpZGF5LWZhY2V0LTMsIGVjaG8gPSBGQUxTRSwgZmlnLndpZHRoID0gNy41fQpnZ3Bsb3Qobm5mLCBhZXMoZGF0ZSwgbikpICsKICAgIGhsYXllciArCiAgICBobGF5ZXIyICsKICAgIGdlb21fbGluZSgpICsKICAgIGZhY2V0X3dyYXAofiB3ZCkgKwogICAgbm5mX3RobQpgYGAKU2hvdyBob2xpZGF5cyBhcyBzb2xpZCBsaW5lcywgZGF5cyBpbiBob2xpZGF5IHdlZWtzIGFzIGRhc2hlZCBsaW5lcy4KCmBgYHtyIGZsaWdodHMtaG9saWRheS1mYWNldC0zLCBldmFsID0gRkFMU0V9CmBgYAoKQSBzaW1wbGUgY2FsZW5kYXIgcGxvdDoKCmBgYHtyIGZsaWdodHMtY2FsLTAsIGVjaG8gPSBGQUxTRX0KbW9udGh3ZWVrIDwtIGZ1bmN0aW9uKGQsIHcpCiAgICBjZWlsaW5nKChkIC0gdykgLyA3KSArIDEKCm5mIDwtIG11dGF0ZShuZiwKICAgICAgICAgICAgIHdkID0gd2RheShkYXRlLCBsYWJlbCA9IFRSVUUpLAogICAgICAgICAgICAgd2QgPSBmY3RfcmV2KHdkKSwKICAgICAgICAgICAgIG13ID0gbW9udGh3ZWVrKGRheSwgd2RheShkYXRlKSkpCgpwIDwtIGdncGxvdChuZiwgYWVzKHggPSBhcy5jaGFyYWN0ZXIobXcpLAogICAgICAgICAgICAgICAgICAgIHkgPSB3ZCwKICAgICAgICAgICAgICAgICAgICBmaWxsID0gbikpICsKICAgIGdlb21fdGlsZShjb2xvciA9ICJ3aGl0ZSIpICsKICAgIGZhY2V0X3dyYXAofiBtb250aChkYXRlLCBsYWJlbCA9IFRSVUUpKQpwCmBgYApUaGlzIHVzZXMgYGdlb21fdGlsZWAgYW5kIGZhY2V0aW5nLgoKYGBge3IgZmxpZ2h0cy1jYWwtMCwgZXZhbCA9IEZBTFNFfQpgYGAKClNvbWUgdGhlbWUgYW5kIGNvbG9yIGFkanVzdG1lbnRzOgoKYGBge3IgZmxpZ2h0cy1jYWwtMSwgZWNobyA9IEZBTFNFfQpwIDwtIHAgKwogICAgc2NhbGVfZmlsbF9ncmFkaWVudChsb3cgPSAid2hpdGUiKSArCiAgICB5bGFiKCIiKSArIHhsYWIoIldlZWsgb2YgTW9udGgiKSArCiAgICB0aGVtZShwYW5lbC5ncmlkLm1ham9yID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgcGFuZWwuYm9yZGVyID0gZWxlbWVudF9ibGFuaygpKQpwCmBgYApgYGB7ciBmbGlnaHRzLWNhbC0xLCBldmFsID0gRkFMU0V9CmBgYAoKVGhpcyBsYXlvdXQgd2l0aCBkYXlzIG9uIHRoZSB2ZXJ0aWNhbCBheGlzIHdvcmtzIHdlbGwgd2l0aCBhIHNpbmdsZSByb3csCndoaWNoIGNvdWxkIGJlIGV4dGVuZGVkIHRvIGEgbXVsdGkteWVhciBwbG90OgoKYGBge3IsIGZpZy5oZWlnaHQgPSAyLCBmaWcud2lkdGggPSAxMH0KcCArIGZhY2V0X3dyYXAofiBtb250aChkYXRlLCBUUlVFKSwgbnJvdyA9IDEpCmBgYAoKQSBtb3JlIHN0YW5kYXJkIGxheW91dDoKCmBgYHtyIGZsaWdodHMtY2FsLTMsIGVjaG8gPSBGQUxTRSwgZmlnLndpZHRoID0gOH0KbmYyIDwtCiAgICBtdXRhdGUobmYsCiAgICAgICAgICAgd2QgPSB3ZGF5KGRhdGUsIGxhYmVsID0gVFJVRSksCiAgICAgICAgICAgbXcgPSBmYWN0b3IobW9udGh3ZWVrKGRheSwKICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgICAgd2RheShkYXRlKSkpLAogICAgICAgICAgIG13ID0gZmN0X3JldihtdykpCgp3ZGxhYnMgPC1zdWJzdHIobGV2ZWxzKG5mMiR3ZCksIDEsIDEpCgpnZ3Bsb3QobmYyLCBhZXMoeCA9IHdkLCB5ID0gbXcsIGZpbGwgPSBuKSkgKwogICAgZ2VvbV90aWxlKGNvbG9yID0gIndoaXRlIikgKwogICAgZmFjZXRfd3JhcCh+IG1vbnRoKGRhdGUsIFRSVUUpKSArCiAgICBzY2FsZV9maWxsX2dyYWRpZW50KGxvdyA9ICJ3aGl0ZSIpICsKICAgIHhsYWIoIiIpICsgeWxhYigiV2VlayBvZiBNb250aCIpICsKICAgIHNjYWxlX3hfZGlzY3JldGUobGFiZWxzID0gd2RsYWJzKSArCiAgICB0aGVtZShwYW5lbC5ncmlkLm1ham9yID0gZWxlbWVudF9ibGFuaygpLAogICAgICAgICAgcGFuZWwuYm9yZGVyID0gZWxlbWVudF9ibGFuaygpKQpgYGAKYGBge3IgZmxpZ2h0cy1jYWwtMywgZXZhbCA9IEZBTFNFLCBmaWcud2lkdGggPSA4fQpgYGAKCgojIyBSZWFkaW5nCgpDaGFwdGVycyBbX1Zpc3VhbGl6aW5nIHRpbWUgc2VyaWVzIGFuZCBvdGhlciBmdW5jdGlvbnMgb2YgYW4KICBpbmRlcGVuZGVudAogIHZhcmlhYmxlX10oaHR0cHM6Ly9jbGF1c3dpbGtlLmNvbS9kYXRhdml6L3RpbWUtc2VyaWVzLmh0bWwpIGFuZAogIFtfVmlzdWFsaXppbmcKICB0cmVuZHNfXShodHRwczovL2NsYXVzd2lsa2UuY29tL2RhdGF2aXovdmlzdWFsaXppbmctdHJlbmRzLmh0bWwpIGluCiAgW19GdW5kYW1lbnRhbHMgb2YgRGF0YQogIFZpc3VhbGl6YXRpb25fXShodHRwczovL2NsYXVzd2lsa2UuY29tL2RhdGF2aXovKS4KCgojIyBFeGVyY2lzZXMKCjEuIEEgdXNlZnVsIGZlYXR1cmUgb2YgdGhlIGBsYXR0aWNlYCBwYWNrYWdlIGlzIHRoZSBhYmlsaXR5IHRvIGVhc2lseQogICAgcmVxdWVzdCBhbiBhc3BlY3QgcmF0aW8gdGhhdCBpcyBfYmFua2VkIHRvIDQ1IGRlZ3JlZXNfIGJ5CiAgICBzcGVjaWZ5aW5nIGBhc3BlY3QgPSAieHkiYCBpbiB0aGUgYXJndW1lbnRzIHRvIGBsYXR0aWNlYCBwbG90dGluZwogICAgZnVuY3Rpb25zLiBGb3IgZXhhbXBsZSwgVGhpcyBjb2RlIHByb2R1Y2VzIGEgcmVhc29uYWJsZSBhc3BlY3QKICAgIHJhdGlvIGZvciBhIHBsb3Qgb2YgYW4gdW5lbXBsb3ltZW50IHRpbWUgc2VyaWVzOgoKICAgIGBgYHtyfQogICAgbGlicmFyeShnZ3Bsb3QyKQogICAgbGlicmFyeShmb3JlY2FzdCkKICAgIGxpYnJhcnkobGF0dGljZSkKICAgIHVuZW1wX3RzIDwtIHRzKGVjb25vbWljcyR1bmVtcGxveSwgc3RhcnQgPSBjKDE5NjcsIDcpLCBmcmVxdWVuY3kgPSAxMikKICAgIHh5cGxvdCh1bmVtcF90cywgYXNwZWN0ID0gInh5IikKICAgIGBgYAoKICAgIFdoaWNoIG9mIHRoZSBmb2xsb3dpbmcgcGxvdHMgbW9zdCBjbG9zZWx5IG1hdGNoZXMgdGhlIGFzcGVjdCByYXRpbwogICAgaW4gdGhlIGBsYXR0aWNlYCBwbG90PwoKICAgIGEuIGBhdXRvcGxvdCh1bmVtcF90cywgYXNwZWN0ID0gMjAwKWAKICAgIGIuIGBhdXRvcGxvdCh1bmVtcF90cykgKyBjb29yZF9maXhlZChyYXRpbyA9IDAuMDAwNylgCiAgICBjLiBgYXV0b3Bsb3QodW5lbXBfdHMpICsgY29vcmRfZml4ZWQoYXNwID0gMC4wMDA3KWAKICAgIGQuIGBhdXRvcGxvdCh1bmVtcF90cykgKyBjb29yZF9maXhlZCg3MClgCg==




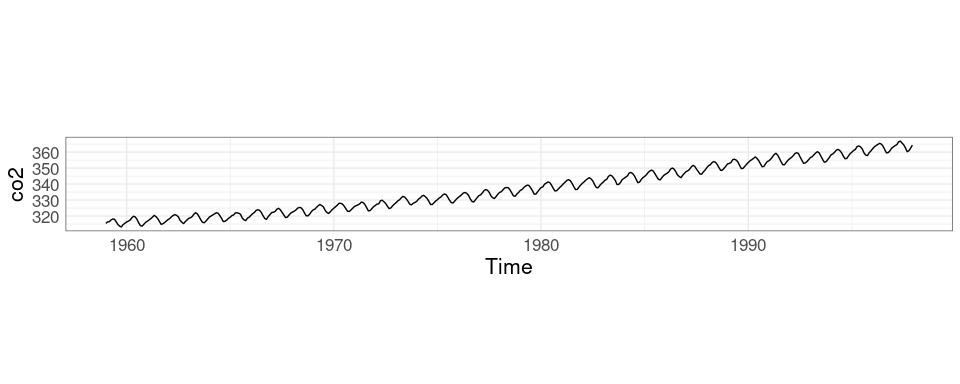 Is there a slowdown in the increase?
Is there a slowdown in the increase?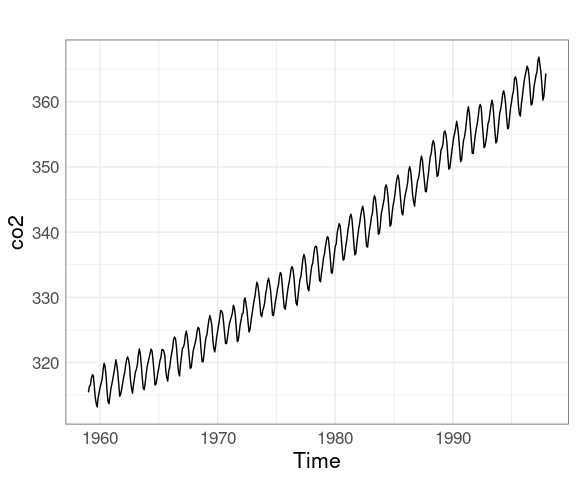





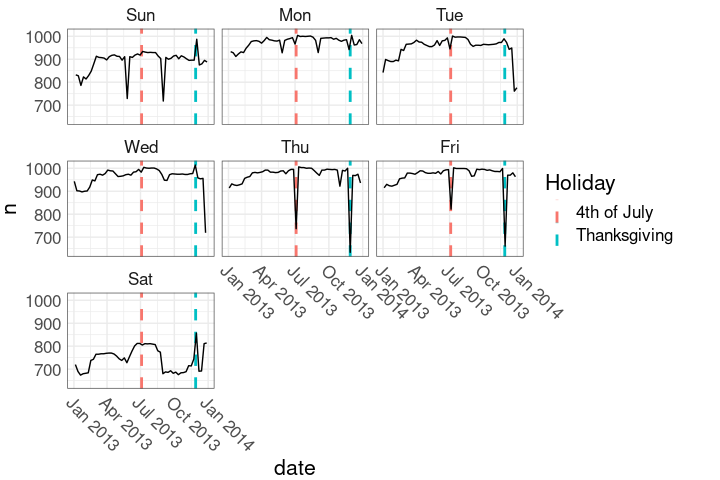
 Show holidays as solid lines, days in holiday weeks as dashed lines.
Show holidays as solid lines, days in holiday weeks as dashed lines. This uses
This uses