The formula for the breakdown given in this problem is only
applicable to monotone ![]() functions. For redescending
functions. For redescending ![]() functions the estimating equation need not have a unique root. To
resolve this one can specify that an estimator should be determined
using a local root finding procedure starting at, say, the sample
median. In this case the M-estimator inherits the 50% breakdown of
the median. See Huber, pages 53-55, for a more complete
discussion.
functions the estimating equation need not have a unique root. To
resolve this one can specify that an estimator should be determined
using a local root finding procedure starting at, say, the sample
median. In this case the M-estimator inherits the 50% breakdown of
the median. See Huber, pages 53-55, for a more complete
discussion.
Solution: The restricted likelihood corresponds to
![]() Bernoulli trials with
Bernoulli trials with ![]() successes and common
success probability
successes and common
success probability ![]() , so the MLE of
, so the MLE of ![]() is
is
![]() . The unrestricted likelihood consists of two
independent sets of Bernoulli trials with success probabilities
. The unrestricted likelihood consists of two
independent sets of Bernoulli trials with success probabilities
![]() and
and ![]() , and the correpsonding MLS's are
, and the correpsonding MLS's are
![]() and
and
![]() . The likelihood ratio statistic
is therefore
. The likelihood ratio statistic
is therefore
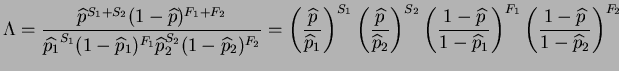 |
and
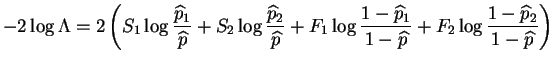 |
The restricted parameter space under the null hypothesis is one-dimensional and the unrestricted parameter space is two-dimensional. Thus under the null hypothesis the distribution of
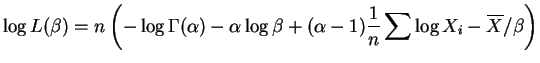 |
So the score function is
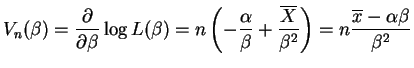 |
and the Fisher information is
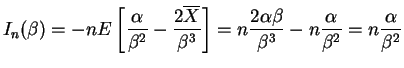 |
So the score statistic is
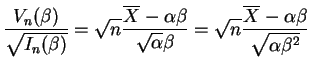 |
