



Next: Solutions
Up: 22S:194 Statistical Inference II
Previous: Solutions
Problem 10.41
Due Friday, May 2, 2003.
Problem: Let
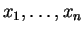 be constants, and suppose
be constants, and suppose
with the
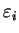 independent
independent
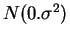 ramdom variables.
ramdom variables.
- a.
- Find the normal equations for the least squares estimators
of
 and
and 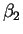 .
.
- b.
- Suppose
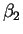 is known. Find the least squares estimator
for
is known. Find the least squares estimator
for  as a function of the data and
as a function of the data and 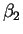 .
.
Due Friday, May 2, 2003.
Problem: Let
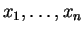 be constants, and suppose
be constants, and suppose
Let 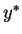 be a constant and let let
be a constant and let let 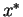 satisfy
satisfy
that is, 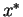 is the value of
is the value of 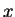 at which the mean response is
at which the mean response is 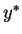 .
.
- a.
- Find the maximum likelihood estimator
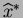 of
of 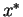 .
.
- b.
- Use the delta method to find the approximate sampling
distribution of
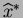 .
.
Due Friday, May 2, 2003.




Next: Solutions
Up: 22S:194 Statistical Inference II
Previous: Solutions
Luke Tierney
2003-05-04

![]() be constants, and suppose
be constants, and suppose
![]() be constants, and suppose
be constants, and suppose
