



Next: Friday, April 18, 2003
Up: Week 12
Previous: Monday, April 14, 2003
Subsections
Class notes and Section 10.2
- Let
 be a random sample that may come from a
Poisson distribution with mean
be a random sample that may come from a
Poisson distribution with mean  . Find the sandwich
estimator of the asymptotic variance of the MLE
. Find the sandwich
estimator of the asymptotic variance of the MLE
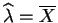 .
.
- Let
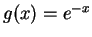 for
for  be an exponential density with
mean one and let
be an exponential density with
mean one and let
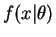 be a
be a
 density. Find
the value
density. Find
the value 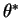 corresponding to the density of the form
corresponding to the density of the form
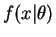 that is closest to
that is closest to 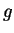 in Kullback-Liebler
divergence.
in Kullback-Liebler
divergence.
Due Friday, April 18, 2003.
Luke Tierney
2003-05-04
