Chapter 5 Optimization
5.1 Preliminaries
Many statistical problems involve minimizing (or maximizing) a function \(f : \mathcal{X} \to \mathbb{R}\), i.e. finding
\[\begin{equation*} x^* = \underset{x \in \mathcal{X}}{\text{argmin}} f(x) \end{equation*}\]
Maximizing \(f(x)\) is equivalent to mimimizing \(-f(x)\).
The domain \(\mathcal{X}\) can be
- a finite set — combinatorial optimization;
- a continuous, usually connected, subset of \(\mathbb{R}^n\).
The function can be
- continuous;
- twice continuously differentiable;
- unrestricted.
The function can
- have a single local minimum that is also a global minimum;
- have one or more local minima but no global minimum;
- have many local minima and a global minimum.
Algorithms can be designed to
- find a local minimum from some specified starting point;
- find the global minimum.
The objective can be
- to find a global minimum;
- to find a local minimum;
- to improve on an initial guess.
Very good software is available for many problems
- general purpose optimizers will often do well;
- occasionally it is useful to write your own, usually to exploit special structure;
- understanding general strategies is useful even when using canned software.
Optimization problems often require some tuning; proper scaling is often critical
5.2 One-Dimensional Optimization
Given an initial point \(x^{(k)}\) and a direction \(d\) we can define
\[\begin{equation*} x(t) = x^{(k)} + t d \end{equation*}\]
and set
\[\begin{equation*} x^{(k+1)} = x^{(k)} + t^* d \end{equation*}\]
where
\[\begin{equation*} t^* = \text{argmin}_t f(x(t)) \end{equation*}\]
with \(t \in \mathbb{R}\) restricted to satisfy \(x(t) \in \mathcal{X}\).
This is often called a line search.
Many one-dimensional optimization methods are available.
Many are based on finding a root of the derivative.
Newton’s method approximates \(f(x(t))\) by a quadratic.
Once the function \(f\) has been minimized in the direction \(d\) a new direction can be tried.
It is usually not necessary to find the minimizer \(t^*\) exactly — a few steps in an iterative algorithm are often sufficient.
R provides
optimizefor minimizing a function over an intervalunirootfor finding the root of a function in an interval
5.3 Choosing Search Directions
Several methods are available for choosing search directions:
Cyclic descent, or coordinate descent: if \(x = (x_1,\dots,x_n)\) then minimize first with respect to \(x_1\), then \(x_2\), and so on through \(x_n\), and repeat until convergence
- This method is also called non-liner Gauss-Seidel iteration or backfitting. It is similar in spirit to Gibbs sampling.
- This may take more iterations than other methods, but often the individual steps are very fast.
A recent paper and the associated
sparsenetpackage takes advantage of this for fitting sparse linear models.Steepest descent, or gradient descent: Take \(d = - \nabla f(x^{(k)})\).
- Steepest descent can be slow to converge due to zig-zagging.
- It can work well for problems with nearly circular contours.
- Preconditioning to improve the shape of the contours can help.
Conjugate gradient: Start with the steepest descent direction and then choose directions conjugate to a strictly positive definite matrix \(A\), often a Hessian matrix.
- This can reduce the zig-zagging.
- It needs to be restarted at least every \(n\) steps.
- Unless the objective function \(f\) is quadratic a new matrix \(A\) is typically computed at each restart.
Most of these methods will be linearly convergent: under suitable regularity conditions and if \(x^{(0)}\) is close enough to a local minimizer \(x^*\) then
\[\begin{equation*} \lim_{k \to \infty} \frac{\|x^{(k+1)} - x^*\|}{\|x^{(k)} - x^*\|} = a \end{equation*}\]
with \(0 < a < 1\); \(a\) is the rate of convergence. A method for which \(a = 0\) is said to converge super-linearly.
5.4 Newton’s Method
Newton’s method approximates \(f\) by the quadratic
\[\begin{equation*} f^{(k)}(x) = f(x^{(k)}) + \nabla f(x^{(k)}) (x - x^{(k)}) + \frac{1}{2} (x - x^{(k)})^T \nabla^2f (x^{(k)}) (x - x^{(k)}) \end{equation*}\]
and computes \(x^{(k+1)}\) to minimize the quadratic approximation \(f^{(k)}\):
\[\begin{equation*} x^{(k+1)} = x^{(k)} - \left(\nabla^2f (x^{(k)})\right)^{-1} \nabla f(x^{(k)}) \end{equation*}\]
Convergence can be very fast: if
- \(f\) is twice continuously differentiable near a local minimizer \(x^*\)
- \(\nabla^2f (x^*)\) is strictly positive definite
- \(x^{(0)}\) is sufficiently close to \(x^*\)
then
\[\begin{equation*} \lim_{k \to \infty} \frac{\|x^{(k+1)}-x^*\|}{\|x^{(k)}-x^*\|^2} = a \end{equation*}\]
with \(0 < a < \infty\). This is called quadratic convergence.
If these conditions fail then Newton’s method may not converge, even for a convex unimodal function.
If the new value \(x^{(k+1)}\) does not improve \(f\) then one can use a line search in the direction of the Newton step.
Newton’s method requires first and second derivatives:
Numerical derivatives can be used.
Computing the derivatives can be very expensive if \(n\) is large.
Many implementations
- modify the second derivative matrix if it is not strictly positive definite;
- switch to an alternate method, such as steepest descent, if the Newton direction does not produce sufficient improvement.
Computation of the Newton step is usually done using a Cholesky factorization of the Hessian.
A modified factorization is often used if the Hessian is not numerically strictly positive definite.
If \(\widetilde{\theta}\) is a consistent estimate of \(\theta\) and \(\widehat{\theta}\) is computed as a single Newton step from \(\widetilde{\theta}\), then, under mild regularity conditions, \(\widehat{\theta}\) will have the same asymptotic normal distribution as the MLE.
5.5 Quasi-Newton Methods
Quasi-Newton methods compute the next step as
\[\begin{equation*} x^{(k+1)} = x^{(k)} - B_k^{-1} \nabla f(x^{(k)}) \end{equation*}\]
where \(B_k\) is an approximation to the Hessian matrix \(\nabla^2 f(x^{(k)})\).
\(B_{k+1}\) is usually chosen so that
\[\begin{equation*} \nabla f(x^{(k+1)}) = \nabla f(x^{(k)}) + B_{k+1} (x^{(k+1)} - x^{(k)}) \end{equation*}\]
For \(n = 1\) this leads to the secant method; for \(n > 1\) this is under-determined.
For \(n > 1\) various strategies for low rank updating of \(B\) are available; often these are based on successive gradient values.
The inverse can be updated using the Sherman-Morrison-Woodbury formula: If \(A\) is invertible then \[\begin{equation*} (A + u v^T)^{-1} = A^{-1}-\frac{A^{-1} uv^T A^{-1}}{1 + v^T A^{-1} u} \end{equation*}\] as long as the denominator is not zero.
Commonly used methods include
- Davidon-Fletcher-Powell (DFP);
- Broyden-Fletcher-Goldfarb-Shanno (BFGS).
Methods generally ensure that
- \(B_k\) is symmetric
- \(B_k\) is strictly positive definite
Convergence of Quasi-Newton methods is generally super-linear but not quadratic.
5.6 Fisher Scoring
Maximum likelihood estimates can be computed by minimizing the negative log likelihood
\[\begin{equation*} f(\theta) = - \log L(\theta) \end{equation*}\]
The Hessian matrix \(\nabla^2 f(\theta^{(k)})\) is the observed information matrix at \(\theta^{(k)}\).
Sometimes the expected information matrix \(I(\theta^{(k)})\) is easy to compute.
The Fisher scoring method uses a Newton step with the observed information matrix replaced by the expected information matrix:
\[\begin{equation*} \theta^{(k+1)} = \theta^{(k)} + I(\theta^{(k)})^{-1} \nabla \log L(\theta^{(k)}) \end{equation*}\]
5.6.1 Example: Logistic Regression
Suppose \(y_i \sim \text{Binomial}(m_i, \pi_i)\) with
\[\begin{equation*} \pi_i = \frac{\exp(x_i^T\beta)}{1 + \exp(x_i^T\beta)} \end{equation*}\]
The negative log likelihood, up to additive constants, is
\[\begin{equation*} f(\beta) = - \sum (y_i x_i^T\beta - m_i \log(1 + \exp(x_i^T \beta)) \end{equation*}\]
with gradient
\[\begin{align*} \nabla f(\beta) &= - \sum \left(y_i x_i - m_i \frac{\exp(x_i^T\beta)}{1 + \exp(x_i^T\beta)} x_i\right)\\ &= - \sum \left(y_i x_i - m_i \pi_i x_i\right)\\ &= - \sum (y_i - m_i \pi_i) x_i \end{align*}\]
and Hessian
\[\begin{equation*} \nabla^2 f(\beta) = \sum m_i \pi_i (1 - \pi_i)x_i x_i^T \end{equation*}\]
The Hessian is non-stochastic, so Fisher scoring and Newton’s method are identical and produce the update
\[\begin{equation*} \beta^{(k+1)} = \beta^{(k)} + \left(\sum m_i \pi_i^{(k)} (1 - \pi_i^{(k)})x_i x_i^T\right)^{-1} \left(\sum (y_i - m_i \pi_i^{(k)}) x_i\right) \end{equation*}\]
If \(X\) is the matrix with rows \(x_i^T\), \(W^{(k)}\) is the diagonal matrix with diagonal elements
\[\begin{equation*} W_{ii}^{(k)} = m_i\pi_i^{(k)} (1 - \pi_i^{(k)}) \end{equation*}\]
and \(V^{(k)}\) is the vector with elements
\[\begin{equation*} V_i^{(k)} = \frac{y_i - m_i \pi_i^{(k)}}{W_{ii}} \end{equation*}\]
then this update can be written as
\[\begin{equation*} \beta^{(k+1)} = \beta^{(k)} + (X^T W^{(k)} X)^{-1} X^T W^{(k)} V^{(k)} \end{equation*}\]
Thus the change in \(\beta\) is the result of fitting the linear model \(V^{(k)} \sim X\) by weighted least squares with weights \(W^{(k)}\).
- This type of algorithm is called an iteratively reweighted least squares (IRWLS) algorithm.
- Similar results hold for all generalized linear models.
- In these models Fisher scoring and Newton’s method are identical when the canonical link function is chosen which makes the natural parameter linear in \(\beta\).
5.7 Gauss-Newton Method
Suppose
\[\begin{equation*} Y_i \sim N(\eta(x_i, \theta), \sigma^2). \end{equation*}\]
For example, \(\eta(x, \theta)\) might be of the form
\[\begin{equation*} \eta(x, \theta) = \theta_0 + \theta_1 e^{-\theta_2 x}. \end{equation*}\]
Then the MLE minimizes
\[\begin{equation*} f(\theta) = \sum_{i=1}^n (y_i - \eta(x_i, \theta))^2. \end{equation*}\]
We can approximate \(\eta\) near a current guess \(\theta^{(k)}\) by the Taylor series expansion
\[\begin{equation*} \eta_k(x_i, \theta) \approx \eta(x_i, \theta^{(k)}) + \nabla_\theta \eta(x_i, \theta^{(k)}) (\theta - \theta^{(k)}) \end{equation*}\]
This leads to the approximate objective function
\[\begin{align*} f_k(\theta) &\approx \sum_{i=1}^n (y_i - \eta_k(x_i, \theta))^2\\ &= \sum_{i=1}^n (y_i - \eta(x_i, \theta^{(k)}) - \nabla_\theta \eta(x_i, \theta^{(k)}) (\theta - \theta^{(k)}))^2 \end{align*}\]
This is the sum of squared deviations for a linear regression model, so is minimized by
\[\begin{equation*} \theta^{(k+1)} = \theta^{(k)} + (J_k^T J_k)^{-1} J_k^T(y - \eta(x, \theta^{(k)})) \end{equation*}\] where \(J_k = \nabla_\theta \eta(x, \theta_{(k)})\) is the Jacobian matrix of the mean function.
The Gauss-Newton algorithm works well for problems with small residuals, where it is close to Newton’s method.
Like Newton’s method it can suffer from taking too large a step.
Backtracking or line search can be used to address this.
An alternative is the Levenberg-Marquardt algorithm that uses
\[\begin{equation*} \theta^{(k+1)} = \theta^{(k)} + (J_k^T J_k + \lambda I)^{-1} J_k^T(y - \eta(x, \theta^{(k)})) \end{equation*}\]
for some damping parameter \(\lambda\). Various strategies for choosing \(\lambda\) are available.
The R function nls uses these approaches.
Nonlinear models are often partially linear. An example:
\[\begin{equation*} y_i = \alpha + \beta \exp\{- x_i / \theta\}. \end{equation*}\]
For a fixed \(\theta\) this is a linear model. So a possible approach is:
- Fix \(\theta\) and estimate \(\alpha\) and \(\beta\) by linear regression.
- Fix \(\alpha\) and \(\beta\) and estimate \(\theta\) by a non-linear method.
- Iterate until convergence.
5.8 Termination and Scaling
Optimization algorithms generally use three criteria for terminating the search:
- relative change in \(x\)
- relative or absolute change in the function values and/or derivatives
- number of iterations
How well these work often depends on problem scaling
- Implementations often allow specification of scaling factors for parameters.
- Some also allow scaling of the objective function.
Dennis and Schnabel (1983) recommend
- a relative gradient criterion \[\begin{equation*} \max_{1 \le i \le n} \left|\frac{\nabla f(x)_i \max\{|x_i|, \text{typ}x_i\}} {\max\{|f(x)|,\text{typ}f\}}\right| \le \epsilon_{\text{grad}} \end{equation*}\] where typ\(x_i\) and typ\(f\) are typical magnitudes of \(x_i\) and \(f\).
- a relative change in \(x\) criterion \[\begin{equation*} \max_{1 \le i \le n} \frac{|\Delta x_i|}{\max\{|x_i|, \text{typ}x_i\}} \le \epsilon_{\text{step}} \end{equation*}\]
Practical use of optimization algorithms often involves
- trying different starting strategies
- adjusting scaling after preliminary runs
- other reparameterizations to improve conditioning of the problem
5.9 Nelder-Mead Simplex Method
This is not related to the simplex method for linear programming!
- The method uses only function values and is fairly robust but can we quite slow and need repeated restarts. It can work reasonably even if the objective function is not differentiable.
- The method uses function values at a set of \(n+1\) affinely independent points in \(n\) dimensions, which form a simplex.
- Affine independence means that the points \(x_1, \dots, x_{n+1}\) are such that \(x_1 - x_{n+1}, \dots, x_n - x_{n+1}\) are linearly independent.
- The method goes through a series of reflection, expansion, contraction , and reduction steps to transform the simplex until the function values do not change much or the simplex becomes very small.
One version of the algorithm, adapted from Wikipedia:
- Order the vertices according to their function values, \[\begin{equation*} f(x_1) \le f(x_2) \le \dots \le f(x_{n+1}) \end{equation*}\]
- Calculate \(x_0 = \frac{1}{n}\sum_{i=1}^n x_i\), the center of the face opposite the worst point \(x_{n+1}\).
- Reflection: compute the reflected point \[\begin{equation*} x_r = x_0 + \alpha (x_0 - x_{n+1}) \end{equation*}\] for some \(\alpha \ge 1\), e.g. \(\alpha = 1\). If \(f(x_1) \le f(x_r) < f(x_n)\), i.e. \(x_r\) is better than the second worst point \(x_n\) but not better than the best point \(x_1\), then replace the worst point \(x_{n+1}\) by \(x_r\) and go to Step 1.
- Expansion: If \(f(x_r) < f(x_1)\), i.e. \(x_r\) is the best point so far, then compute the expanded point \[\begin{equation*} x_e = x_0 + \gamma (x_0 - x_{n+1}) \end{equation*}\] for some \(\gamma > \alpha\), e.g. \(\gamma = 2\). If \(f(x_e) < f(x_r)\) then replace \(x_{n+1}\) by \(x_e\) and go to Step 1. Otherwise replace \(x_{n+1}\) with \(x_r\) and go to Step 1.
- Contraction: If we reach this step then we know that \(f(x_r) \ge f(x_n)\). Compute the contracted point \[\begin{equation*} x_c = x_0 + \rho (x_0 - x_{n+1}) \end{equation*}\] for some \(\rho < 0\), e.g. \(\rho = -1/2\). If \(f(x_c) < f(x_{n+1})\) replace \(x_{n+1}\) by \(x_c\) and go to Step 1. Otherwise go to Step 6.
- Reduction: For \(i = 2, \dots, n+1\) set \[\begin{equation*} x_i = x_1 + \sigma (x_i - x_1) \end{equation*}\] for some \(\sigma < 1\), e.g. \(\sigma = 1/2\).
The Wikipedia page shows some examples as animations.
5.10 Simulated Annealing
Simulated annealing is motivated by an analogy to slowly cooling metals in order to reach the minimum energy state.
It is a stochastic global optimization method.
It can be very slow but can be effective for difficult problems with many local minima.
For any value \(T > 0\) the function
\[\begin{equation*} f_T(x) = e^{f(x)/T} \end{equation*}\]
has minima at the same locations as \(f(x)\).
Increasing the temperature parameter \(T\) flattens \(f_T\); decreasing \(T\) sharpens the local minima.
Suppose we have a current estimate of the minimizer, \(x^{(k)}\) and a mechanism for randomly generating a proposal \(y\) for the next estimate.
A step in the simulated annealing algorithm given a current estimate \(x^{(k)}\):
- Generate a proposal \(y\) for the next estimate.
- If \(f(y) \le f(x^{(k)})\) then accept \(y\) and set \(x_{(k+1)} = y\).
- If \(f(y) > f(x^{(k)})\) then with probability \(f_T(x^{(k)}) / f_T(y)\) accept \(y\) and set \(x_{(k+1)} = y\).
- Otherwise, reject \(y\) and set \(x_{(k+1)} = x_{(k)}\).
- Adjust the temperature according to a cooling schedule and repeat.
Occasionally accepting steps that increase the objective function allows escape from local minima.
A common way to generate \(y\) is as a multivariate normal vector centered at \(x_{(k)}\). A common choice of cooling schedule is of the form \(T = 1 / \log(k)\).
The standard deviations of the normal proposals may be tied to the current temperature setting.
Under certain conditions this approach can be shown to converge to a global minimizer with probability one.
Using other forms of proposals this approach can also be used for discrete optimization problems.
5.11 EM and MCEM Algorithms
Suppose we have a problem where complete data \(X,Z\) has likelihood
\[\begin{equation*} L^c(\theta|x,z) = f(x,z|\theta) \end{equation*}\]
but we only observe incomplete data \(X\) with likelihood
\[\begin{equation*} L(\theta|x) = g(x|\theta) = \int f(x,z|\theta) dz \end{equation*}\]
Often the complete data likelihood is much simpler than the incomplete data one.
The conditional density of the unobserved data given the observed data is \[\begin{equation*} k(z|x, \theta) = \frac{f(x,z|\theta)}{g(x|\theta)} \end{equation*}\]
Define, taking expectations with respect to \(k(z|x,\phi)\),
\[\begin{align*} Q(\theta|\phi,x) &= E_\phi[\log f(x,z|\theta)|x]\\ H(\theta|\phi,x) &= E_\phi[\log k(z|x, \theta)|x] \end{align*}\]
The EM algorithm consists of starting with an initial estimate \(\widehat{\theta}^{(0)}\) and repeating two steps until convergence:
- E(xpectation)-Step: Construct \(Q(\theta|\widehat{\theta}^{(i)})\)
- M(aximization)-Step: Compute \(\widehat{\theta}^{(i+1)}=\text{argmax}_\theta\; Q(\theta|\widehat{\theta}^{(i)})\)
This algorithm was introduced by Dempster, Laird and Rubin (1977); it unified many special case algorithms in the literature.
The EM algorithm increases the log likelihood at every step; this helps to ensure a very stable algorithm.
The EM algorithm is typically linearly convergent.
Acceleration methods may be useful. Givens and Hoeting describe some; others are available in the literature.
If \(Q(\theta|\phi,x)\) cannot be constructed in closed form, it can often be computed by Monte Carlo methods; this is the MCEM algorithm of Wei and Tanner (1990).
In many cases MCMC methods will have to be used in the MCEM algorithm.
5.11.1 Example: Normal Mixture Models
Suppose \(X_1, \dots, X_n\) are independent and identically distributed with density
\[\begin{equation*} f(x|\theta) = \sum_{j = 1}^M p_j f(x|\mu_j, \sigma_j^2) \end{equation*}\]
with \(p_1, \dots, p_M \ge 0\), \(\sum p_j = 1\), and \(f(x|\mu,\sigma^2)\) is a Normal\((\mu, \sigma^2)\) density. \(M\) is assumed known.
We can think of \(X_i\) as generated in two stages:
- First a category \(J\) is selected from \(\{1, \dots, M\}\) with probabilities \(p_1, \dots, p_M\).
- Then, given \(J = j\), a normal random variable is generated from \(f(x|\mu_j,\sigma_j^2)\).
We can represent the unobserved category using indicator variables
\[\begin{equation*} Z_{ij} = \begin{cases} 1 & \text{if $J_i = j$}\\ 0 & \text{otherwise.} \end{cases} \end{equation*}\]
The complete data log likelihood is
\[\begin{equation*} \log L(\theta | x, z) = \sum_{i=1}^n\sum_{j=1}^M z_{ij}\left[\log p_j - \log \sigma_j - \frac{1}{2}\left(\frac{x_i - \mu_j}{\sigma_j}\right)^2\right] \end{equation*}\]
The Expectation step produces
\[\begin{equation*} Q(\theta|\widehat{\theta}^{(k)}) = \sum_{i=1}^n\sum_{j=1}^M \widehat{p}_{ij}^{(k)}\left[\log p_j - \log \sigma_j - \frac{1}{2}\left(\frac{x_i - \mu_j}{\sigma_j}\right)^2\right] \end{equation*}\]
with
\[\begin{equation*} \widehat{p}_{ij}^{(k)} = E[Z_{ij}|X = x, \theta^{(k)}] = \frac{\widehat{p}_j^{(k)} f\left(x_i\left|\widehat{\mu}_j^{(k)}, \widehat{\sigma}_j^{(k)2}\right.\right)} {\sum_{\ell = 1}^M \widehat{p}_\ell^{(k)} f\left(x_i\left|\widehat{\mu}_\ell^{(k)}, \widehat{\sigma}_\ell^{(k)2}\right.\right)} \end{equation*}\]
The Maximization step then produces
\[\begin{align*} \widehat{\mu}_j^{(k+1)} &= \frac{\sum_{i=1}^n \widehat{p}_{ij}^{(k)} x_i} {\sum_{i=1}^n \widehat{p}_{ij}^{(k)}}\\ \widehat{\sigma}_j^{(k+1)2} &= \frac{\sum_{i=1}^n \widehat{p}_{ij}^{(k)} (x_i - \widehat{\mu}_j^{(k+1)})^2} {\sum_{i=1}^n \widehat{p}_{ij}^{(k)}}\\ \widehat{p}_j^{(k+1)} &= \frac{1}{n} \sum_{i=1}^n \widehat{p}_{ij}^{(k)} \end{align*}\]
A simple R function to implement a single EM step might be written as
EMmix1 <- function(x, theta) {
mu <- theta$mu
sigma <- theta$sigma
p <- theta$p
M <- length(mu)
## E step
Ez <- outer(x, 1 : M, function(x, i) p[i] * dnorm(x, mu[i], sigma[i]))
Ez <- sweep(Ez, 1, rowSums(Ez), "/")
colSums.Ez <- colSums(Ez)
## M step
xp <- sweep(Ez, 1, x, "*")
mu.new <- colSums(xp) / colSums.Ez
sqRes <- outer(x, mu.new, function(x, m) (x - m)^2)
sigma.new <- sqrt(colSums(Ez * sqRes) / colSums.Ez)
p.new <- colSums.Ez / sum(colSums.Ez)
## pack up result
list(mu = mu.new, sigma = sigma.new, p = p.new)
}Some notes:
- Reasonable starting values are important.
We want a local maximum near a good starting value, not a global maximum.
Code to examine the log likelihood for a simplified example is available
Some recent papers:
- Tobias Ryden (2008). EM versus Markov chain Monte Carlo for estimation of hidden Markov models: a computational perspective, Bayesian Analysis 3 (4), 659–688.
- A. Berlinet and C. Roland (2009). Parabolic acceleration of the EM algorithm. Statistics and Computing 19 (1), 35–48.
- Chen, Lin S., Prentice, Ross L., and Wang, Pei (2014). A penalized EM algorithm incorporating missing data mechanism for Gaussian parameter estimation, Biometrics 70 (2), 312–322. %% **** data example?
5.11.2 Theoretical Properties of the EM Algorithm
The conditional density of the unobserved data given the observed data is
\[\begin{equation*} k(z|x, \theta) = \frac{f(x,z|\theta)}{g(x|\theta)} \end{equation*}\]
Define, taking expectations with respect to \(k(z|x,\phi)\),
\[\begin{align*} Q(\theta|\phi,x) &= E_\phi[\log f(x,z|\theta)|x]\\ H(\theta|\phi,x) &= E_\phi[\log k(z|x, \theta)|x] \end{align*}\]
For any \(\phi\)
\[\begin{equation*} \log L(\theta|x) = Q(\theta|\phi,x) - H(\theta|\phi,x) \end{equation*}\]
since for any \(z\)
\[\begin{align*} \log L(\theta|x) &= \log g(x|\theta)\\ &= \log f(x,z|\theta) - \log f(x, z|\theta) + \log g(x|\theta)\\ &= \log f(x,z|\theta) - \log \frac{f(x,z|\theta)}{g(x|\theta)}\\ &= \log f(x, z|\theta) - \log k(z|x,\theta) \end{align*}\]
and therefore, taking taking expectations with respect to \(k(z|x,\phi)\),
\[\begin{align*} \log L(\theta|x) &= E_\phi[\log f(x, z|\theta)] - E_\phi[\log k(z|x,\theta)]\\ &= Q(\theta|\phi,x) - H(\theta|\phi,x) \end{align*}\]
Furthermore, for all \(\theta\)
\[\begin{equation*} H(\theta|\phi) \le H(\phi|\phi) \end{equation*}\]
since, by Jensen’s inequality,
\[\begin{align*} H(\theta|\phi) - H(\phi|\phi) &= E_\phi[\log k(z|x,\theta)] - E_\phi[\log k(z|x,\phi)]\\ &= E_\phi\left[\log\frac{k(z|x,\theta)}{k(z|x,\phi)}\right]\\ &\le \log E_\phi\left[\frac{k(z|x,\theta)}{k(z|x,\phi)}\right]\\ &= \log \int \frac{k(z|x,\theta)}{k(z|x,\phi)} k(z|x,\phi) dz\\ &= \log \int k(z|x,\theta) dz = 0. \end{align*}\]
This implies that for any \(\theta\) and \(\phi\)
\[\begin{equation*} \log L(\theta|x) \ge Q(\theta|\phi,x) - H(\phi|\phi,x) \end{equation*}\]
with equality when \(\theta = \phi\), and therefore
if \(\widehat{\theta}\) maximizes \(L(\theta|x)\) then \(\widehat{\theta}\) maximizes \(Q(\theta|\widehat{\theta},x)\) with respect to \(\theta\):
\[\begin{align*} Q(\theta|\widehat{\theta},x) - H(\widehat{\theta}|\widehat{\theta},x) &\le \log L(\theta|x)\\ &\le \log L(\widehat{\theta}|x) = Q(\widehat{\theta}|\widehat{\theta},x) - H(\widehat{\theta}|\widehat{\theta},x) \end{align*}\]
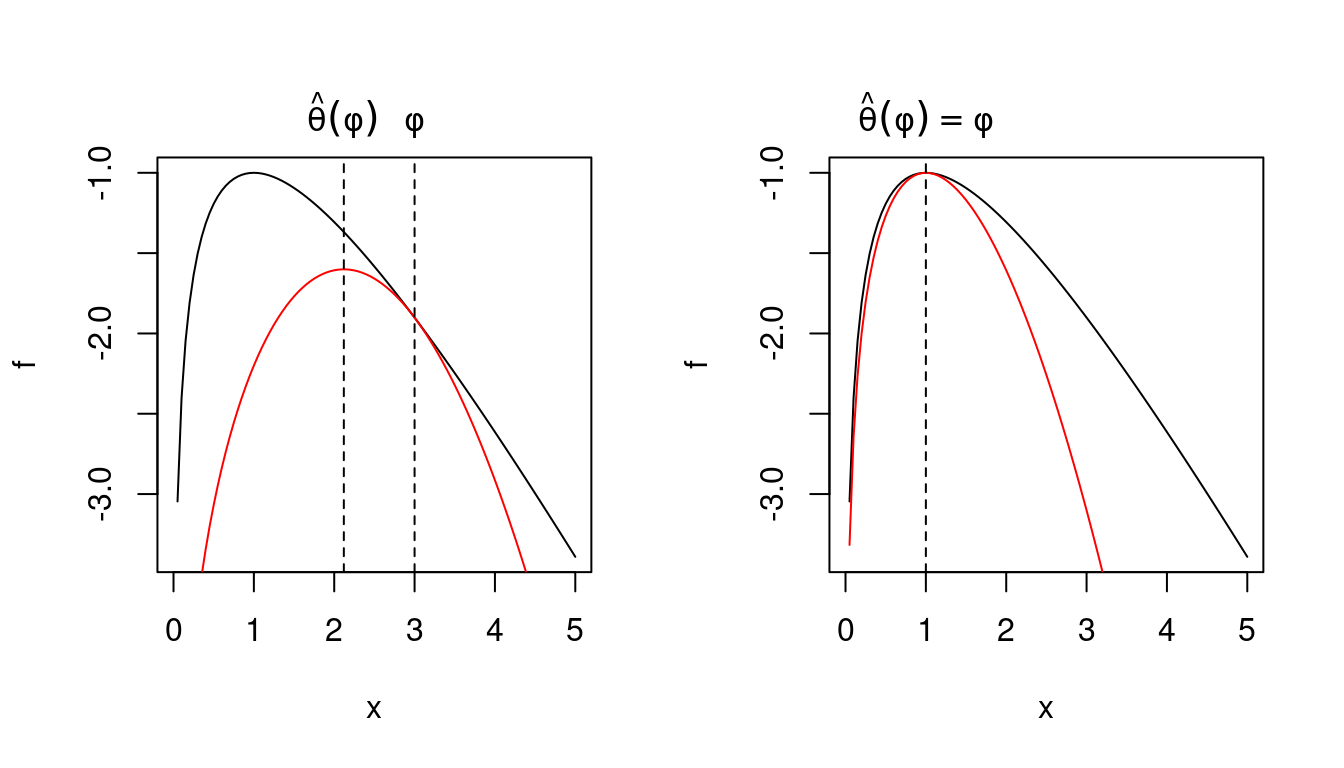
if \(\widehat{\theta}(\phi)\) maximizes \(Q(\theta|\phi,x)\) for a given \(\phi\) then \(\log L(\phi|x) \le \log L(\widehat{\theta}(\phi)| x)\):
\[\begin{align*} \log L(\phi|x) &= Q(\phi|\phi,x) - H(\phi|\phi,x)\\ &\le Q(\widehat{\theta}(\phi)|\phi,x) - H(\phi| \phi,x)\\ & \le Q(\widehat{\theta}(\phi)|\phi,x) - H(\widehat{\theta}(\phi)| \phi,x)\\ & = \log L(\widehat{\theta}(\phi)| x) \end{align*}\]
In the following figures the black curve corresponds to \(\log L(\theta|x)\) and the red curve to the surrogate function \(Q(\theta|\phi, x) - H(\phi|\phi, x)\).
5.12 MM Algorithms
The EM algorithm can be viewed as a special case of an MM algorithm.
MM stands for
- Minimization and Majorization, or
- Maximization and Minorization.
Suppose the objective is to maximize a function \(f(\theta)\).
The assumption is that a surrogate function \(g(\theta | \phi)\) is available such that
\[\begin{equation*} f(\theta) \ge g(\theta|\phi) \end{equation*}\]
for all \(\theta, \phi\), with equality when \(\theta = \phi\).
The function \(g\) is said to minorize the function \(f\).
The MM algorithm starts with an initial guess \(\widehat{\theta}^{(0)}\) and then computes
\[\begin{equation*} \widehat{\theta}^{(i + 1)} = \text{argmax}_\theta g(\theta|\widehat{\theta}^{(i)}) \end{equation*}\]
As in the EM algorithm,
- if \(\widehat{\theta}\) maximizes \(f(\theta)\), then \(\widehat{\theta}\) maximizes \(g(\theta|\widehat{\theta})\);
- if \(\widehat{\theta}(\phi)\) maximizes \(g(\theta|\phi)\), then \[\begin{equation*} f(\phi) \le f(\widehat{\theta}(\phi)). \end{equation*}\]
The objective function values will increase, and under reasonable conditions the algorithm will converge to a local maxizer.
Full maximization of \(g\) is not needed as long as sufficient progress is made (single Newton steps are often sufficient).
The art in designing an MM algorithm is finding a surrogate minorizing function \(g\) that
- produces an efficient algorithm
- is easy to maximize
In \(p\)-dimensional problems it is often possible to choose minorizing functions of the form
\[\begin{equation*} g(\theta|\phi) = \sum_{j=1}^p g_j(\theta_j|\phi) \end{equation*}\]
so that \(g\) can be maximized by separate one-dimensional maximizations of the \(g_j\).
5.12.1 Example: Bradley Terry Model
In the Bradley Terry competition model each team has a strength \(\theta_i\) and
\[\begin{equation*} P(\text{$i$ beats $j$}) = \frac{\theta_i}{\theta_i + \theta_j} \end{equation*}\]
with \(\theta_1 = 1\) for identifiability.
Assuming independent games in which \(y_{ij}\) is the number of times \(i\) beats \(j\) the log likelihood is
\[\begin{equation*} \log L(\theta) = \sum_{i,j} y_{ij} \left(\log(\theta_i) - \log(\theta_i+\theta_j)\right) \end{equation*}\]
Since the logarithm is concave, for any \(x\) and \(y\)
\[\begin{equation*} -\log y \ge -\log x - \frac{y-x}{x} \end{equation*}\]
and therefore for any \(\theta\) and \(\phi\)
\[\begin{align*} \log L(\theta) &\ge \sum_{i,j} y_{ij} \left(\log(\theta_i) - \log(\phi_i+\phi_j) - \frac{\theta_i+\theta_j-\phi_i-\phi_j}{\phi_i+\phi_j}\right)\\ &= g(\theta|\phi)\\ &= \sum_i g_i(\theta_i|\phi) \end{align*}\]
with
\[\begin{equation*} g_i(\theta_i|\phi) = \sum_j y_{ij}\log\theta_i - \sum_j(y_{ij}+y_{ji})\frac{\theta_i-\phi_i}{\phi_i+\phi_j}. \end{equation*}\]
The parameters are separated in \(g\), and the one-dimensional maximizers can be easily computed as
\[\begin{equation*} \widehat{\theta}_i(\phi) = \frac{\sum_{j} y_{ij}}{\sum_{j}(y_{ij}+y_{ji})/(\phi_i+\phi_j)} \end{equation*}\]
Some References on MM algorithms:
- Hunter DR and Lange K (2004), A Tutorial on MM Algorithms, The American Statistician, 58: 30-37.
- Lange, K (2004). Optimization, Springer-Verlag, New York.
5.13 Gradient Descent Methods
Gradient descent, or steepest descent, methods have one advantage: only the gradient needs to be computed.
A simple gradient descent approach uses
\[ x_{n+1} = x_n - \alpha \nabla f(x_n). \]
For a quadratic function \(f(x) = \frac{1}{2} x^T A x - x^T b\) with strictly positive definite second derivative matrix \(A\) this algorithm converges linearly if
\[ \alpha < \frac{2}{\rho(A)} \]
where \(\rho(A)\) is the spectral radius of \(A\), i.e. the largest eigenvalue.
The optimal choice of \(\alpha\) is
\[ \alpha = \frac{2}{\rho(A)} \times \frac{\kappa(A)}{\kappa(A) + 1} \]
where \(\kappa(A)\) is the condition number of \(A\).
The corresponding rate of convergence is
\[ \frac{\kappa - 1}{\kappa + 1}. \]
This provides some guidance for use in the non-quadratic case:
- \(\alpha\) needs to be small enough but not too small;
- making sure the problem is well-conditioned is very important.
The step size \(\alpha\) can be chosen adaptively by a line search or by backtracking, e.g. starting with \(\alpha = \alpha_0\) and reducing \(\alpha\) by a factor of 1/2 until
\[ f(x - \alpha \nabla f(x)) > f(x) - \frac{1}{2}\alpha\|\nabla f(x)\|^2 \]
Other adaptive strategies try to avoid evaluating \(f(x)\).
Momentum methods try to reduce zig-zagging by using a combination of the previous step direction and the current gradient.
Stochastic gradient descent methods try to reduce the cost of each step in cases where
\[ f(x) = \frac{1}{n} \sum_{i=1}^n f_i(x) \]
by at each step choosing a sample \(i_1, \dots, i_m\) and computing the gradient of
\[ \frac{1}{m} \sum_{k=1}^m f_{i_k}(x). \]
Choosing \(m = 1\) sometimes works.
Variants of Stochastic gradient descent are used widely in machine learning algorithms, in particular for fitting deep neural networks.
In machine learning the step size \(\alpha\) is called the learning rate.
Stochastic gradient descent will converge almost surely under mild conditions if used with a learning rate decay, e.g. with a learning rate \(\alpha_k\) at iteration \(k\) of the form
\[ \alpha_k = \alpha_0 \frac{1}{1 + \delta k}. \]
5.14 Constrained Optimization
Equality constraints arise, for example, in
- restricted maximum likelihood estimation needed for the null hypothesis in likelihood ratio tests
- estimating probabilities that sum to one
Inequality constraints arise in estimating
- probabilities or rates that are constrained to be non-negative
- monotone functions or monotone sets of parameters
- convex functions
Box constraints are the simplest and the most common.
Linear inequality constraints also occur frequently.
Inequality constraints are often handled by converting a constrained problem to an unconstrained one:
- Minimizing \(f(x)\) subject to \(g_i(x) \ge 0\) for \(i = 1, \dots, M\) is equivalent to minimizing \[\begin{equation*} F(x) = \begin{cases} f(x) & \text{if $g_i(x) \ge 0$ for $i = 1, \dots, M$ }\\ \infty & \text{otherwise.} \end{cases} \end{equation*}\]
- This objective function is not continuous.
Sometimes a complicated unconstrained problem can be changed to simpler constrained one.
5.14.1 Example: \(L_1\) Regression
The \(L_1\) regression estimator is defined by the minimization problem
\[\begin{equation*} \widehat{b} = \underset{b}{\text{argmin}} \sum |y_i - x_i^T b| \end{equation*}\]
This unconstrained optimization problem with a non-differentiable objective function can be reformulated as a constrained linear programming problem:
For a vector \(z = (z_1, \dots, z_n)^T\) let \([z]_+\) denote the vector of positive parts of \(z\), i.e.
\[\begin{equation*} ([z]_+)_i = \max(z_i, 0) \end{equation*}\]
and let
\[\begin{align*} b_+ &= [b]_+\\ b_- &= [-b]_+\\ u &= [y - Xb]_+\\ v &= [Xb - y]_+ \end{align*}\]
Then the \(L_1\) estimator satisfies
\[\begin{equation*} \widehat{b} = \underset{b}{\text{argmin}} \; \mathbf{1}^T u + \mathbf{1}^T v \end{equation*}\]
subject to the constraints
\[\begin{align*} &y = Xb_+ - Xb_- + u - v\\ &u \ge 0, v \ge 0, b_+ \ge 0, b_- \ge 0 \end{align*}\]
This linear programming problem can be solved by the standard simplex algorithm.
A specialized simplex algorithm taking advantage of structure in the constraint matrix allows larger data sets to be handled (Barrodale and Roberts, 1974).
Interior point methods can also be used and are effective for large \(n\) and moderate \(p\).
An alternative approach called smoothing is based on approximating the absolute value function by a twice continuously differentiable function and can be effective for moderate \(n\) and large \(p\).
Chen and Wei (2005) provide an overview in the context of the more general quantile regression problem.
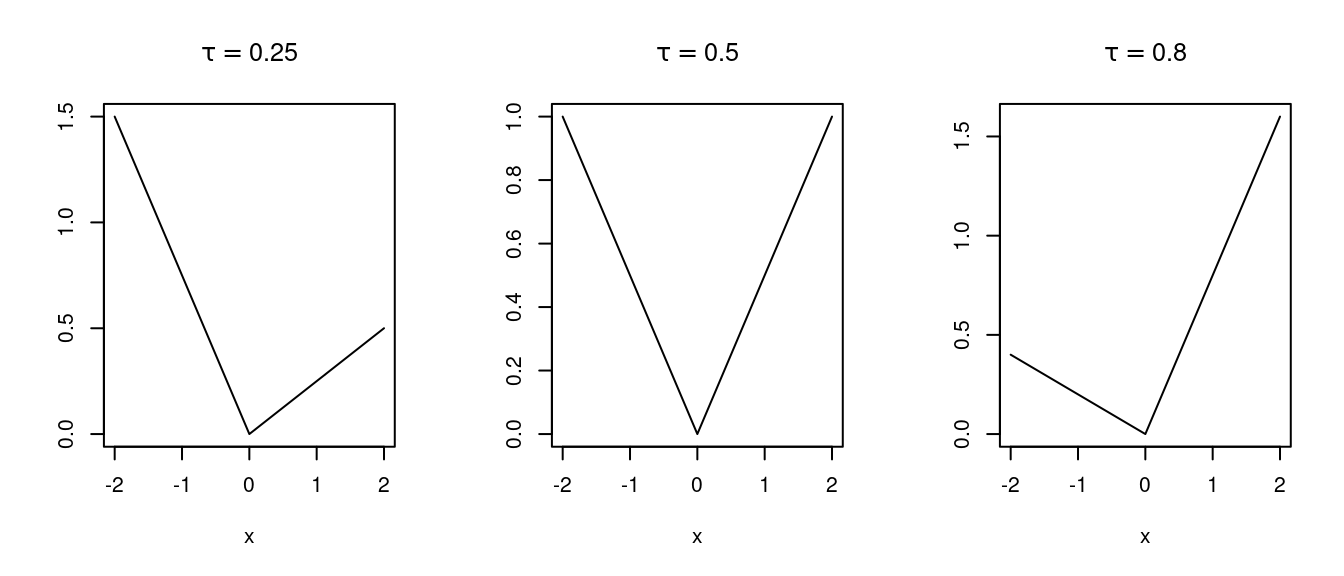
Quantile regression computes estimates as \[\begin{equation*} \widehat{b} = \underset{b}{\text{argmin}} \sum \rho_\tau(y_i - x_i^Tb) \end{equation*}\] with \[\begin{equation*} \rho_\tau(y) = y\left(\tau - 1_{\{y < 0\}}\right) = \tau [y]_+ + (1 - \tau) [-y]_+. \end{equation*}\] for \(0 < \tau < 1\). For \(\tau = \frac{1}{2}\) this is \(\rho_{\frac{1}{2}}(y) = \frac{1}{2}|y|\).
Reformulation as a constrained optimization problem is also sometimes used for LASSO and SVM computations.
5.14.2 Some Approaches and Algorithms
If the optimum is in the interior of the feasible region then using standard methods on \(F\) may work, especially if these use backtracking if they encounter infinite values.
For interior optima transormations to an unbounded feasible region may help.
Standard algorithms can often be modified to handle box constraints.
Other constraints are often handled using barrier methods that approximate \(F\) by a smooth function
\[\begin{equation*} F_\gamma(x) = \begin{cases} f(x) - \gamma \sum_{i = 1}^M \log g_i(x) & \text{if $g(x) \ge 0$}\\ \infty & \text{otherwise} \end{cases} \end{equation*}\]
for some \(\gamma > 0\). The algorithm starts with a feasible solution, minimizes \(F_\gamma\) for a given \(\gamma\), reduces \(\gamma\), and repeats until convergence.
Barrier methods are also called path-following algorithms.
Path-following algorithms are useful in other settings where a harder problem can be approached through a sequence of easier problems.
Path-following algorithms usually start the search for the next \(\gamma\) at the solution for the previous \(\gamma\); this is sometimes called a warm start approach.
The intermediate results for positive \(\gamma\) are in the interior of the feasible region, hence this is an interior point method
More sophisticated interior point methods are available in particular for convex optimization problems.
5.14.3 An Adaptive Barrier Algorithm
Consider the problem of minimizing \(f(x)\) subject to the linear inequality constraints
\[\begin{equation*} g_i(x) = b_i^T x - c_i \ge 0 \end{equation*}\]
for \(i = 1, \dots, M\). For an interior point \(x^{(k)}\) of the feasible region define the surrogate function
\[\begin{equation*} R(x | x^{(k)}) = f(x) - \mu \sum_{i=1}^M \left[g_i(x^{(k)}) \log(g_i(x)) - b_i^T x\right] \end{equation*}\]
for some \(\mu > 0\). As a function of \(x\) the barrier function
\[\begin{equation*} f(x) - R(x | x^{(k)}) = \mu \sum_{i=1}^M \left[g_i(x^{(k)}) \log(g_i(x)) - b_i^T x\right] \end{equation*}\]
is concave and maximized at \(x = x^{(k)}\). Thus if
\[\begin{equation*} x^{(k+1)} = \underset{x}{\text{argmin}} \; R(x | x^{(k)}) \end{equation*}\]
then
\[\begin{align*} f(x^{(k+1)}) & = R(x^{(k+1)}|x^{(k)}) + f(x^{(k+1)}) - R(x^{(k+1)}|x^{(k)})\\ &\le R(x^{(k)}|x^{(k)}) + f(x^{(k+1)}) - R(x^{(k+1)}|x^{(k)})\\ &\le R(x^{(k)}|x^{(k)}) + f(x^{(k)}) - R(x^{(k)}|x^{(k)})\\ & = f(x^{(k)}) \end{align*}\]
The values of the objective function are non-increasing.
This has strong similarities to an EM algorithm argument.
The coefficient of a logarithmic barrier term decreases to zero if \(x^{(k)}\) approaches the boundary.
If \(f\) is convex and has a unique minimizer \(x^*\) then \(x^{(k)}\) converges to \(x^*\).
This algorithm was introduced in K. Lange (1994).
5.15 Optimization in R
Several optimization functions are available in the standard R distribution:
optimimplements a range of methods:- Nelder-Mead simplex
- Quasi-Newton with the BFGS update
- A modified Quasi-Newton BFGS algorithm that allows box constraints
- A conjugate gradient algorithm
- A version of simulated annealing.
- Some notes:
- A variety of iteration control options are available.
- Analytical derivatives can be supplied to methods that use them.
- Hessian matrices at the optimum can be requested.
nlminbprovides an interface to the FORTRAN PORT library developed at Bell Labs. Box constraints are supported.nlmimplements a modified Newton algorithm as described in Dennis and Schnabel (1983).constrOptimimplements the adaptive barrier method of Lange (1994) usingoptimfor the optimizations within iterations.
The Optimization Task View on CRAN describes a number of other methods available in contributed packages.
Simple examples illustrating optim and constrOptim
are available.